2. Понятие лотереи.

Формально говоря, в предыдущей игре исход для пер­вого игрока - это не число, а более сложный объект - выигрыш, зависящий от случая. В жизни с такими вещами постоянно приходится сталкиваться. Примеры - рулетки, лотереи, карточные игры, лошадиные бега, спортивные игры и т.п. Урожай зависит от капризов погоды, выручка - от конъюнкту­ры. Страхование - целая индустрия, построенная на неопределенности. Как же оценивать такие неопределенные вещи. Далее мы ограничимся тем случа­ем, когда существуют вероятности наступления того или иного исхода. Для контраста стоит отметить, что в играх приходится иметь дело с неопреде­ленностью более суровой, чем вероятностная - это неопределенность выбора стратегий партнерами по игре. Можно ли считать, что их действия всегда можно описать в вероятностных терминах?

Исход, зависящий от случая, формализуется понятием лотереи, или слу­чайного исхода. Пусть дано множество X ’’чистых” исходов; простоты ра­ди будем считать X конечным. Тогда лотерея тт (на X) задается указанием вероятностей π(х) наступления каждого исхода х £ X. Числа тт(х) неотри­цательные и в сумме равны нулю. Итак, лотерея - это просто формальная комбинация вида ^2хк(х) <g) ж, где х пробегает X, π(х) > 0 для любого х и ^2хк(х) = 1. На более математическом языке это вероятностная мера на X. Носителем лотереи (меры) 7г называется подмножество supp(7r) = {х £ X, 7г(х) 0}.

Лотереи рисуют схемами типа

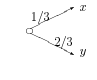
Вопросы для самоконтроля:

1. Что называется случайным ходом? Приведите примеры.

2. Что называется лотереей? Приведите примеры.

Список литературы

Основная:

1. Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.

2. Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.

3. Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.

4. Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.

Дополнительная:

1. Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.

2. Саакян Г.Р. Лекции. Теория игр [Текст] : электронный учебник/ Г.Р. Саакян .- Шахты, 2006.

Лекция № 16-17 Равновесия Нэша.

Цель: изучить одно из самых важнейших понятий теории игр – равновесие Нэша.

Ключевые слова: равновесие Нэша.

Вопросы:

1. Игра в нормальной форме;

2. Определение равновесия;

3. Выпуклые игр;

4. Примеры.

1. Игра в нормальной форме

Определение. Игрой n лиц в нормальной форме называется набор <N,U1,…,Un,g1,…,gn>, где N={1,…,n} - множество, содержащее n элементов, U1,…,U_n - произвольные множества, g1,…,gn - функции, каждая из которых отображает произведение U₁ … U_n в множество действительных чисел .

Числа i N интерпретируются как номера игроков, множество U_i представляет собой множество управлений игрока i, а функция g_i - его критерий.

Нормальная форма подразумевает, что, выбирая свое управление, каждый игрок не имеет никакой информации о выборах своих партнеров по игре.

Набор u=(u₁,…,u_n) управлений всех игроков будем называть ситуацией в рассматриваемой игре. Множество всех ситуаций U₁ … U_n будем обозначать буквой U без индекса.

Если не оговорено противное, то термин "стратегия" будет использоваться как полный синоним термина "управление", а термин "исход" - как синоним термина "ситуация".

Каждой антагонистической игре <U,V,g> можно естественным образом сопоставить игру двух лиц общего вида <{1,2},U,V,g,-g>.

Практически все результаты, полученные для антагонистических игр, с очевидными изменениями переносятся на класс игр с постоянной суммой, то есть таких игр двух лиц <{1,2},U1,U2,g1,g2>, у которых сумма g1(u1,u2)+g2(u1,u2) не зависит от (u1,u2).

То же относится и к более широкому классу квазиантагонистических игр двух лиц, то есть таких игр, для которых каждая точка (u1,u2) U1 U2 является эффективной.