Вопросы для самоконтроля:

1. Что понимается под групповым выбором решения?

2. В чем заключается содержание проблемы группового выбора?

3. Сформулируйте постановку задачи группового выбора.

4. Назовите принципы группового выбора и охарактеризуйте их.

5. Что такое “V-оптимальное решение”?

6. Какие различают типы отношений между коалициями? Каково

7. их содержание?

8. Как осуществляется многокритериальный выбор решений?

9. Как может быть осуществлен выбор единственного решения при групповом ЛПР?

Список литературы

Основная:

1. Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.

2. Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.

3. Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.

4. Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.

Дополнительная:

1. Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.

2. Саакян Г.Р. Лекции. Теория игр [Текст] : электронный учебник/ Г.Р. Саакян .- Шахты, 2006.

Лекция №14-15. Случайные ходы и лотереи.

Цель: изучить особенности решения лотерей и игр со случайными ходами.

Ключевые слова: случайный ход, лотерея.

Вопросы:

1. Случайные ходы.

2. Понятие лотереи.

1. Случайные ходы.

Имеется еще один источник неопределенности игроков относительно состояния позиции - случай. Например, в карточных играх игроки обычно не знают карты партнеров (недаром их тщательно перетасо­вывают перед раздачей), и это тоже нужно отразить в описании игры. Одна­ко, в отличие от предыдущей неопределенности, эта неопределенность носит вероятностный характер и имплантируется сравнительно легко. Формально просто к списку игроков добавляется фиктивный игрок - природа, которая тоже выбирает свои ходы, но делает это не свободно, как обычные игроки, а с предписанными вероятностями.

Для примера рассмотрим следующую пародию на ’’покер”. Первый игрок (Ваня) получает карту, которая в 1/6 случаев благоприятна для него. По­смотрев карту, он может либо ’’повысить ставку” (Д), либо ’’спасовать” (Р). Во втором случае игра заканчивается, и Ваня отдает второму игроку (Маше) 10 р. В первом случае Маша, не видя карты, может либо ’’принять повыше­ние” (г), либо тоже ’’спасовать” (р). Выигрыши Вани (так как игра с нулевой суммой) в различных ситуациях приведены на рисунке ниже.

З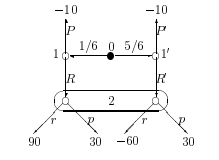 десь у Вани два информационных множества 1 и 1; а у Маши - одно (так как она не видит карту).

Можно ли по такой игре образовать нормальную форму? Со стратегиями особых проблем нет. Снова каждый игрок должен решить, как он ведет се­бя (какой ход выбирает) в каждом своем информационном множестве. Ваня должен решить - что он делает при хорошей карте (в позиции 1) и что – при плохой, в позиции V. Так что у него 4 стратегии: RR\ RP'7 PR' и РР'. У Маши - две стратегии: г и р.

А вот с выигрышами возникает некоторая проблема. Допустим, Ваня вы­брал стратегию RR', а Маша - г. Если карта хорошая, Ваня получает 90 р., если плохая - теряет 60 р. Как же оценить его выигрыш? Простейший выход - посчитать математическое ожидание 90 • 1/6 — 60 • 5/6 = —35. Аналогично можно заполнить остальные клеточки.