
- •Расчетно-графическая работа №1
- •Минимизация геометрическим методом
- •Минимизация методом карт Карно
- •Минимизация методом Квайна.
- •Минимизация методом Квайна-Мак-Класки.
- •Минимизация методом неопределенных коэффициентов.
- •Минимизация методом минимизирующих карт
- •2.1 Минимизация методом карт Карно
- •2.2 Минимизация методом Квайна.
- •2.3 Минимизация методом Квайна-Мак-Класки.
Федеральное агентство по образованию
ГОУ ВПО «Ижевский государственный технический университет»
факультет «Прикладной математики»
кафедра «Прикладная математика и информатика»
Расчетно-графическая работа №1
Минимизация функции алгебры логики
(Вариант № 16)
Выполнила: студент группы Б04-281-1
Чайников М. А.
Проверил: проф. каф. ПМИ
Калядин Н. И.
Ижевск, 2014
Задача №1
Формулировка:
Записать формулу функции F и минимизировать ее геометрическим
методом, методом карт Карно, Квайна,
Квайна-Мак-Класки, неопределенных
коэффициентов, минимизирующих карт.
Сравнить результаты.
и минимизировать ее геометрическим
методом, методом карт Карно, Квайна,
Квайна-Мак-Класки, неопределенных
коэффициентов, минимизирующих карт.
Сравнить результаты.
Практическая часть.
Функция задана следующей таблицей истинности
|
|
|
F |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
Представим ее в совершенной дизъюнктивной нормальной форме
F
СДНФ=
Минимизация геометрическим методом
О тметим
на рис.1 вершины, соответствующие
конъюнкциям, входящим в СДНФ данной
функции.
тметим
на рис.1 вершины, соответствующие
конъюнкциям, входящим в СДНФ данной
функции.
З
Рис. 1


x2

x1
x2
аметим, что четыре вершины лежат в одной грани.Откуда следует, что минимальная форма функции
F
МДНФ=
Минимизация методом карт Карно
Построим карту Карно, соответствующую данной функции, где каждая клетка карты соответствует членам СДНФ функции.
x1 x2x3 |
00 |
01 |
11 |
10 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
1 |
После склеивания элементов получим минимальную форму функции.
F МДНФ =
Минимизация методом Квайна.
Запишем первичные импликаты в 1-й столбец таблицы, занумеруем их. Применим закон склеивания, результат запишем во 2-й столбец таблицы, снова занумеруем их, склеенные члены 1-го столбца отметим звездочками.
Члены F |
Результаты 1-го склеивания |
Результаты 2-го склеивания |
1
|
1
|
1
|
2
|
2
|
|
3
|
3
|
3
|
4
|
4
|
|
5
|
5
|
|
6
|
6
|
|
|
7
|
|
Несклеившиеся простые импликанты обводим рамочкой. Дизъюнкция их дает сокращенную ДНФ. В данном примере 1-й этап сразу приводит к цели: F МДНФ= есть минимальная форма функции.









 *
* (1,2)*
(1,2)* (1,5)
(1,5) *
* (1,3)*
(1,3)* *
* (1,5)*
(1,5)* (2,7)
(2,7) *
* (2,4)*
(2,4)* *
* (3,4)*
(3,4)*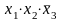 *
* (3,6)*
(3,6)* (5,6)*
(5,6)*