Вариант № 30
1. Найти производные функций:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
2. Найти производные функций, используя логарифмическое дифференцирование:
1.
2.
3. Найти и функций:
1.
2.
в точке
.
4. Написать уравнения касательной и нормали к графику
функции в точке .
5. Точка
движется прямолинейно по закону
.
Найти скорость, ускорение и путь,
пройденный точкой при
6. Найти
приближенное значение функции
.
7. Провести полное исследование функций, построить их графики:
1.
2.
.
8. Требуется построить котел, состоящий из цилиндра, завершенного двумя полусферами, со стенками постоянной толщины так, чтобы при данной вместимости на его изготовление пошло наименьшее количество материала.
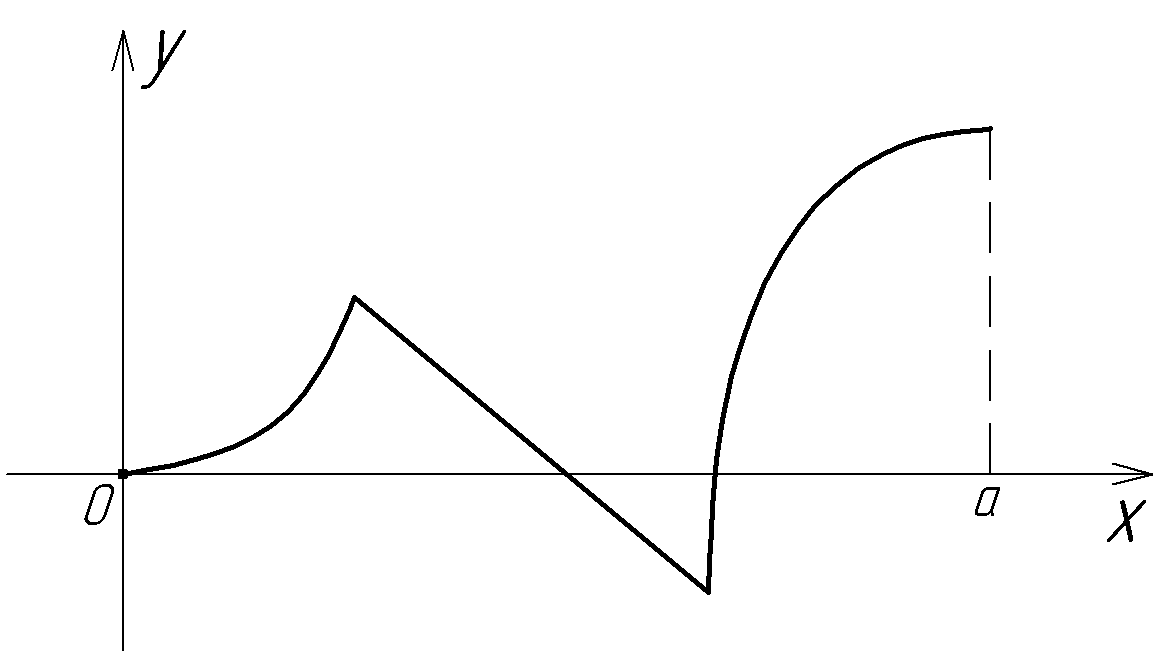
9. По графику функции построить эскизы графиков первой и второй производных.
Вариант № 31*
1. Найти производные функций:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
2. Найти производные функций, используя логарифмическое
дифференцирование:
1.
2.
3. Найти и функций:
1.
2.
4. Написать
уравнения касательной и нормали к
графику функции
5. Точка
движется прямолинейно по закону
.
Найти скорость, ускорение и путь,
пройденный точкой при
6. Найти
приближенное значение функции
.
7. Провести полное исследование функций, построить их графики:
1.
2.
8. Скорость
течения воды по круглой трубе прямо
пропорциональна гидравлическому радиусу
,
вычисляемому по формуле
,
где
- площадь сечения потока воды в трубе,
- смоченный (подводный) периметр сечения
трубы. Степень заполнения трубы
характеризуется центральным углом,
опирающимся на горизонтальную поверхность
текущей воды. При какой степени заполнения
трубы скорость течения воды будет
наибольшей?
Указание: корни получающегося при решении трансцендентного уравнения можно найти либо графически, либо одним из численных методов.
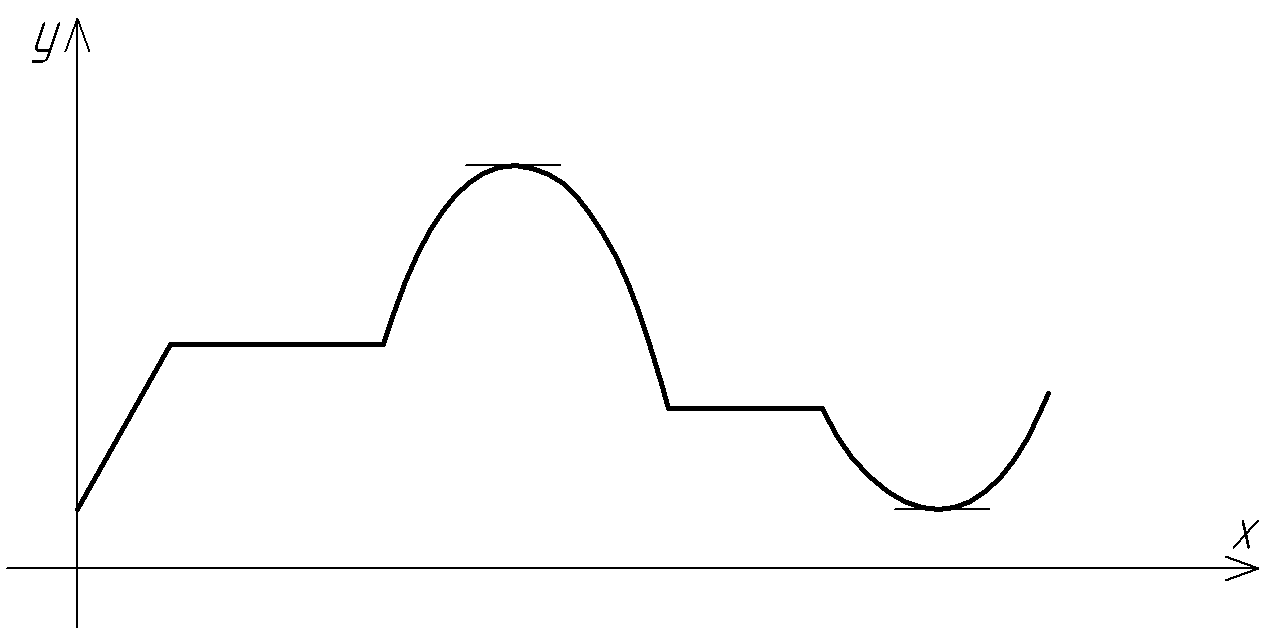
9. По графику функции построить эскизы графиков первой и второй производных.
Вариант № 32*
1. Найти производные функций:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
2. Найти производные функций, используя логарифмическое дифференцирование:
1.
2.
3. Найти и функций:
1.
2.
4. Написать
уравнения касательной и нормали к
графику функции
в точке
.
5. Точка
движется прямолинейно по закону
.
Найти скорость, ускорение и путь,
пройденный точкой при
6. Найти приближенное значение функции .
7. Провести полное исследование функций, построить их графики:
1.
2.
.
8. Канал, ширина которого 27 м, под прямым углом впадает в другой канал шириною 64 м. Какова может быть наибольшая длина бревен, которые можно сплавлять по этой системе каналов?
9.
По графику функции построить эскизы
графиков первой и второй производных.
