Задачи для самостоятельного решения

3.1. Определить индукцию магнитного поля в центре соленоида, со­держащего 500 витков, если сила тока в обмотке соленоида равна 10 А. Длина соленоида равна 20 см, его диаметр - 4 см. Формулу магнитной индукции бесконечного соленоида считать неприменимой.

3.2. В центре кругового витка радиуса 30 см индукция магнитного поля равна 20 мкТл. Вычислить магнитную индукцию на его оси в точке, расположенной на расстоянии 40 см от плоскости витка.

3.3. Принимая, что электрон в водородоподобном атоме движется со скоростью 4 Мм/с по круговой орбите радиусом 0,1 нм. Опре­делить индукцию магнитного поля в её центре.

3.4. Индукция маг­нитного поля в точке, расположенной на оси кругового контура радиуса 0,5 м на расстоянии 50 см от его плоскости, равна 4 мкТл. Определить силу тока в контуре.

3.5. Вычислить индукцию магнитного поля в центре квадратного кон­тура со стороной 20 см, по которому протекает ток 10 А.

3.6. Контур с током имеет форму правильного шестиугольника со стороной 10 см. Определить силу тока в контуре, если индукция магнитного поля в центре контура равна 20 мкТл.

3 .7. Длинный тонкий проводник, по которому течёт ток 20 А, изогнут под прямым углом. Определить индукцию магнитного поля тока в точке, лежащей на биссектрисе прямого угла на расстоянии 14,1 см от его вершины.

3 .8. Два одинаковых круговых витка радиусом 10 см имеют общую ось. Расстояние между центрами витков равно 20 см. Токи в витках равны 10 А и противоположно направлены. Определить индукцию магнитного поля в середине отрезка, соединяющего центры витков.

3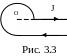 .9. Тонкий длинный проводник с током 5 А изогнут под прямым углом так, что изгиб имеет форму четверти окружности радиусом 10 см. Определять индукцию магнитного поля тока в центре этой окружности.

3.10. Бесконечный прямой проводник образует виток радиусом 50 см. Определить ток в проводнике, если индукция магнитного поля в центре витка равна 40 мкТл (рис. 3.1).

3 .11. Длинный прямой проводник с током 10 А имеет изгиб в виде квадрата, сторона которого равна 20 см. Определить индукцию магнитного поля в точке А, расположенной в центре изгиба (рис. 3.2).

3.12. Бесконечно длинный проводник, по которому течет ток 5 А, изогнут так, как показано на рис. 3.3. Радиус изогнутой части равен 0,1 м. Определить индукцию магнитного поля тока в точке О.

3 .13. Определить индукцию магнитного поля в точке О контура, по которому течёт ток 20 А. Контур изображен на рис. 3.4. R = 0,1 м.

3 .14. Длинный проводник, по которому течёт ток 15 А, имеет вид, показанный на рис. 3.5. Радиус полуокружности R = 20 см. Определить индукцию магнитного поля тока в точке О.

3.15. Вычислить индукцию магнитного поля тока в точке 0 контура, показанного на рис.3.6. Ток в контуре равен 5 A, R = 10 см.

3.16. Определить индукцию магнитного поля тока в точке 0 контура, показанного на рис.3.7. Ток в контуре равен 10 А, R = 20 см, φ = 120⁰.

3 .17. Длинный проводник, по которому течёт ток 20 А, изогнут под прямым углом. Найти индукцию магнитного поля в точке, которая лежит на перпендикуляре к проводникам, восстановленным в точке изгиба, и удалена от плоскости проводника на расстояние 0,5 м.

3.18. Тонкое кольцо радиусом 10 см, равномерно заряженное с ли­нейной плотностью заряда 0,2 мкКл/м, вращается с постоянной угловой скоростью 5 рад/с вокруг перпендикулярна к плоскости кольца и проходящего через его геометрический центр. Определить индукцию магнит­ного поля в центре кольца.

3.19. По двум прямолинейным бесконечным проводам, образующим вза­имно перпендикулярные скрещивающиеся прямые, текут токи 5 А и 10 А. Расстояние между проводами равно 20 см. Определить индукцию магнитного поля токов в точке, лежащей посредине между проводами.

3.20. Два длинных прямолинейных проводника с токами 10 А и 15 А расположены в одной плоскости так, что угол между направлениями токов равен 60⁰. Определить индукцию магнитного поля токов в точке, лежащей на биссектрисе этого угла на расстоянии 20 см от его вершины.

3.21. Электрон движется прямолинейно с постоянной скоростью 6 м/с. Определить максимальную индукцию магнитного поля, создаваемого электроном, в точке, отстоящей от его траектории движения на 1 мм.

3.22. Тонкий диск радиусом 10 см, равномерно заряженный с поверх­ностной плотностью заряда 0,2 мкКл/м², вращается с постоянной угловой скоростью 10 рад/с вокруг оси, перпендикулярной плоскости диска и проходящей через его геометрический центр. Определить индукцию маг­нитного поля в центре диска.

3.23.Два протона движутся параллельно друг другу с одинаковой скоростью 600 км/с. Найти отношение сил электрического и магнитного взаимодействия этих частиц.

3.24. Два равных точечных заряда 0,1 мкКл движутся навстречу друг другу со скоростью 100 км/с. Найти индукцию магнитного поля движущихся зарядов в точке на расстоянии 4 см от первого заряда и на расстоянии 3 см от второго в тот момент, когда расстояние между ними равно 5 см.

3.25. Два одинаковых точечных заряда 0,2 мкКл движутся в одной плоскости вдоль взаимно- перпендикулярных прямых. Скорости зарядов рав­ны 2 Мм/с и 3 Мм/с. В некоторый момент времени заряды оказываются на одинаковом расстоянии 10 см от точки пересечения их траекторий движе­ния, удаляясь от этой точки. Определить в этот момент времени индукции магнитного поля этих зарядов в точке пересечения их траекторий.

3.26. Пользуясь теоремой о циркуляции вектора индукции магнитного поля, вычислить расстояние, на котором бесконечный прямолинейный ток 10 А создает магнитное поле индукцией 0,1 мкТл.

3.27. По тонкой трубе радиусом 2 см течет ток 20 А. Определить индукцию магнитного поля тока на расстояниях 1 см и 4 см от оси трубы.

3.28. В прямолинейном проводнике радиусом 4 см протекает ток с постоянной плотностью 800 А/м². Определить индукцию магнитного поля тока на расстоянии 5 см от оси проводника тока.

3.29. Ток 100 А течет по длинному прямому проводнику радиусом 5 см. Определить индукцию магнитного поля в точке на расстоянии 2 см от оси проводника. Считать, что проводник изготовлен из немагнитного материала, а рас­пределение тока равномерно по его сечению.

3.30. По тонкой длинной трубе протекает ток 10 А. На оси трубы расположен тонкий проводник, по которому течет ток 6 А в обратном направлении. Определить индукцию магнитного поля токов вне трубы на расстоянии 20 см от ее оси.

3.31. По двум коаксиальным тонкостенным трубам радиусами 10 см и 30 см текут токи соответственно 50 А и 100 А в противоположных направ­лениях. Найти индукцию магнитного поля в точках на расстояниях 20 см и 40 см от общей оси труб.

3.32. На оси тонкостенной трубы радиусом 10 см расположен тонкий проводник, по которому течет ток 10 А. По трубе течет ток 40 А в том же направлении. Найти расстояние от оси трубы до точки, в которой индук­ция магнитного поля токов такая же, как и на расстоянии 5 см от оси трубы.

3.33. По длинной трубе с внутренним радиусом 3 см и внешним 4 см протекает ток с постоянной по сечению плотностью тока 500 А/м². Определить индукцию магнитного поля в точке на расстоянии 10 см от оси трубы.

3.34. Воздушный соленоид длиной 0,2 м и радиусом 0,3 см имеет 300 витков. Ток в соленоиде 5 А. Применяя теорему о циркуляции вектора индукции магнит­ного поля, вычислить индукцию магнитного поля тока внутри соленоида. Счи­тать поле однородным и заключенным лишь внутри соленоида.

3.35. На два длинных коаксиальных цилиндра радиусами 3 см и 5 см намотаны проводники равного диаметра - 0,5 мм - так, что соседние витки прилегают плотно друг к другу. По проводникам пропускают токи 20 А и 30 А соответственно для внутреннего и внешнего цилиндров. Направления токов одинаковы. Пользуясь теоремой о циркуляции вектора индукции магнитного поля, вычислить магнитную индукцию в точке на расстоянии 4 см от общей оси цилиндров.

3.36. По обмотке воздушного тороида, содержащей 1000 витков, течет ток силой 5 А. Внутренний радиус тороида равен 8 см, внешний - 12 см. Определить индукцию магнитного поля в точках на средней линии тороида.

3.37. По длинному прямому проводнику круглого поперечного сечения радиусом 2 см протекает ток 100 А, равномерно распределенный по его сечению. Вычислить циркуляцию вектора индукции магнитного поля тока по контуру, имеющему форму квадрата со стороной 1 см. Центр контура лежит на оси проводника, а его плоскость перпендикулярна к этой оси. Магнит­ная проницаемость проводника равна 1.

3.38. По проводнику круглого поперечного сечения радиусом 0,2 см течет ток, равномерно распределенный по сечению с плотностью тока 800 А/м². Определить циркуляцию вектора индукции магнитного поля по контуру в виде правильного треугольника, вписанного в сечение провод­ника. Проводник изготовлен из диамагнитного материала.

3.39. По прямолинейному проводнику круглого поперечного сечения радиусом 0,2 см течет ток, распределенный по сечению с постоянной плотностью тока 2000 А/м². Определить, на каком расстоянии от оси проводни­ка вне его индукция магнитного поля тока такая же, как и на расстоянии 0,1 см. Магнитную проницаемость материала проводника считать равной 1.

3.40. По обмотке тороида, имеющего 3000 витков, течет ток силой 10 А. Определить индукцию магнитного поля в точке, расположенной внут­ри тороида на расстоянии 20 см от центра тороида. Сердечник в тороиде отсутствует.

3.41. По бесконечной плоскости течет ток одного направления. Ли­нейная плотность тока, т.е. ток, приходящийся на единицу длины в нап­равлении, перпендикулярном к току, равна 100 А/м. Пользуясь теоремой о циркуляции вектора индукции магнитного поля, определить модуль вектора индукции магнитного поля. Доказать, что поле однородно с обеих сторон от плоскости.

3.42. По проводнику круглого сечения течет ток, равномерно рас­пределенный по сечению. Найти отношение циркуляции вектора индукции магнитного поля по двум контурам: по окружности, ограничивающей сече­ние проводника, и квадрату, вписанному в эту окружность.

3.43. По тонкостенной длинной трубе течёт ток 10 А. По оси трубы расположен тонкий проводник, по которому течет ток 2 А в обрат­ном направлении. Радиус трубы 3 см. На каком расстоянии от оси трубы вне ее магнитная индукция такая же, как и на расстояния 1 см?

3.44. Тороид содержит 800 витков. Наружный диаметр тороида равен 20 см, внутренний - 10 см. Ток, протекающий по обмотке тороида, равен 10 А. Определить максимальное значение магнитной индук­ции в тороиде.

3.45. В условиях предыдущей задачи определить минимальное зна­чение магнитной индукции в тороиде.

3.46. Тонкий проводник с током 5 А расположен на общей оси двух тонкостенных труб радиусами 2 см и 5 см, по которым текут токи соотве­тственно 2 А и 3 А. Токи текут в одном направлении. Определить значе­ние индукции магнитного поля на расстоянии 4 см от проводника.

3.47. Ток 10 А течет по длинной тонкостенной трубе радиусом 5 см и возвращается по сплошному проводнику радиусом 1 мм, расположенному на оси трубы. Определить индукцию магнитного поля на рас­стоянии 2 см от оси трубы.

3.48. По длинному прямолинейному проводнику круглого поперечного сечения диаметром 0,8 см течет ток, равномерно распределенный по сече­нию проводника. Определить силу тока в проводнике, если индукция маг­нитного поля в точке, расположенной на расстоянии 0,2 см от оси про­водника, равна 1 мТл.

3.49. Длинный соленоид имеет квадратное сечение 0,5 х 0,5 см² и 2000 витков на каждом метре длины. По обмотке соленоида течет ток 20 А. Определить индукцию магнитного поля в средней точке на оси соленоида.

3.50. По длинной трубе с внутренним диаметром 5 см и внешним 7 см течет ток, равномерно распределенный по сечению трубы. На оси трубы расположен тонкий проводник с током 10 А. Определить направление и плотность тока в трубе, при которых индукция магнитного поля вне трубы будет равна нулю.

3 .51. Ток 20 А течет по длинному прямому проводнику, сечение ко­торого имеет форму тонкого по­лукольца (рис. 3.8). Плотность тока постоянна по сечению, R = 0,1 м. Определить индукцию магнитного поля в точке 0.

3.52. Непроводящая сфера радиусом 10 см, равномерно заряженная с поверхностной плотностью заряда 5 мкКл/м², вращается с угловой ско­ростью 20 рад/с вокруг оси, проходящей через ее центр. Найти индукцию магнитного поля в центре сферы.

3.53. Тонкостенный цилиндр радиусом 5 см и высотой 10 см, равно­мерно заряженный с поверхностной плотностью заряда 10 мкКл/м², враща­ется с угловой скоростью 10 рад/с вокруг собственной оси. Определить индукцию магнитного поля в средней точке на оси цилиндра.

3.54. Два протона движутся параллельно друг другу с одинаковой скоростью 2 Мм/с на расстоянии 20 см друг от друга. Определить макси­мальную индукцию магнитного поля в плоскости, проходящей через середи­ну отрезка, соединяющего протоны, перпендикулярно к плоскости, в кото­рой находятся траектории движения протонов.

З.55. Плотность тока внутри неограничен­ной пластины толщиной 2 см равна 600 А/м². Найти индукцию магнитного поля этого тока на расстоянии 0,5 см от середины пластины. Магнитную проницаемость вещества пластины считать равной единице.

3 .56. Ток 10 А равномерно распределен по сечению длинного цилиндра радиусом 5 см. Ток 20 А течет по тонкому кольцу радиусом 10 см, ось которого совпадает с осью цилиндра (рис.3.9). Найти индукцию магнитного поля токов в точке А на оси цилинд­ра, отстоящей на расстоянии 10 см от плоскости кольца.

3.57. Вектор индукции магнитного поля направлен вдоль оси у, в его градиент - вдоль оси х. Замкнутый контур в виде квадрата со сто­роной 10 см расположен в плоскости ху так, что одна его сторона па­раллельна оси х. Определить циркуляцию вектора индукции магнитного поля по данному контуру, если градиент поля dB/dx = 5 Тл/м, причем В = 0 при x = 0.

3.58. Плотность тока j как функция расстояния r от оси аксиальносимметричного параллельного потока электронов имеет вид j = αr, где α = 500 А/м. Определить индукцию магнитного поля на расстоянии 0,5 м от оси симметрии потока электронов.

3.59. По безграничной плоскости течет ток с линейной плотностью тока 20 А/см (плотность тока дана в направлении, перпендикулярном к направле­нию вектора плотности тока). Над плоскостью выбран контур в форме квад­рата со стороной 10 см, две стороны которого параллельны плоскости, а две другие стороны составляют угол 30⁰ с нормалью к плоскости. Опреде­лить циркуляцию вектора индукции магнитного поля по заданному контуру.

3.60. В прямом бесконечном проводнике круглого поперечного сече­ния радиусом 0,2 см плотность тока от расстояния до оси проводника г задана законом j = а/r, где а - 50 А/м. Определить индукцию магнитного поля в точках, расположенных на расстояниях 0,1 см и 0,5 см от оси проводника.