Материалы для контрольной работы №3 (электродинамика)

1. Движение заряженных частиц в электрическом и магнитном полях

Сила, действующая на точечный заряд Q в электрическом поле:

, где  напряженность электрического поля.

Работа сил электрического поля по перемещению точечного заряда Q:

А = Q(₁ - ₂) = Q,

где₁ и ₂  потенциалы электрического поля в начальной и конечной точках.

Потенциальная энергия взаимодействия двух точечных зарядов:

,

где k = 910⁹ м/Ф, r  расстояние между зарядами.

Сила, действующая на точечный заряд Q, движущийся в магнитном поле (сила Лоренца):

,

где  скорость заряженной частицы,  индукция магнитного поля.

Модуль силы Лоренца

F_лор=QBsin,

где   угол между вектором скорости и вектором магнитной индукции, причем и .

Примеры решения задач

Задача 1. Протон, ускоренный разностью потенциалов  = 100 В, влетает в плоский воздушный конденсатор параллельно его пластинам. Длина пластин конденсатора L = 0,2 м, расстояние между ними d = 0,05 м. Найти: 1) смещение при вылете из конденсатора относительно первоначального направления y; 2) скорость протона при вылете . Напряжение на конденсаторе U = 20 В. Масса протона m = 1,6710^-27 кг, заряд протона Q = 1,610^19 Кл.

Решение.

Рассмотрим движение протона до влета в конденсатор. По теореме о кинетической энергии работа сил электростатического поля:

,

где _н, ₀  начальная и конечная скорости протона в ускоряющем электрическом поле (по условию задачи _н = 0).

С другой стороны, она равна А_эл = Q,

где  = ускоряющая разность потенциалов.

Тогда . Следовательно, начальная скорость протона при влете в конденсатор .

Внутри конденсатора на протон действует сила электрического поля .

Электрическое поле заряженного конденсатора однородное, поэтому напряженность поля равна E=U/d.

В ыберем систему координат хоy, как показано на рисунке 1-а. По второму закону Ньютона

или .

В проекции на ось оy: QE = ma, т.е. ускорение протона равно а = QЕ/m = QU/(md).

Координаты протона в момент времени t равны:

x = ₀t – смещение вдоль оси ox;

y = at²/2 - смещение вдоль оси оy.

По истечении времени пролета протоном конденсатора x = L, y =y. Время движения в конденсаторе равно

Смешение при вылете .

y = 200,2²/(40,05100) = 0,04 м.

Скорость протона в момент вылета ,

где _х = ₀, .

Следовательно, .

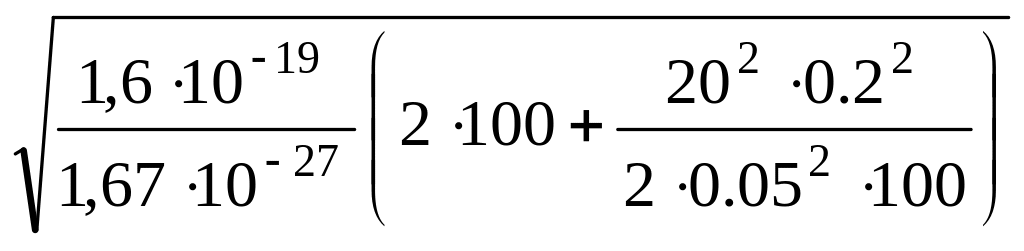 = = 1,410⁵ м/с.

Ответ: y = 0,04 м,  = 1,410⁵ м/с.

З адача 2. Из состояния покоя электрон движется по направлению к центру равномерно заряженного шара радиусом R = 0,1 м, с зарядом Q = 2 НКл. Начальное расстояние электрона до поверхности шара h = 2,9 м. Найти скорость электрона, с которой он приблизится к поверхности шара. Удельный заряд электрона Q₁/m = 1,7610¹¹ Кл/кг.

Решение.

По закону сохранения энергии

W_n1 = W_n2 + W_к ,

где ,  начальная и конечная потенциальные энергии электорона в электричесом поле заряда Q; W_k = m²/2 – кинетическая энергия электрона у поверхности шара, Q₁ = -1,610^-19 Кл –заряд электрона, m = 9,110^-31 кг – масса электрона.

Найдем скорость электрона у поверхности шара

.

 = = 7,610⁶ м/с.

Ответ:  = 7,610⁶ м/с.

Задача 3. Протон движется в однородном магнитном поле с индукцией В = 0,2 Тл. Траектория его движения  винтовая линия с радиусом R = 0,1 м и шагом h = 0,5 м. Найти скорость протона. Заряд протона Q = 1,610^-19 Кл, масса протона m = 1,6710^-27 кг.

Решение.

Сложное движение протона по винтовой линии можно представить как сумму двух движений: поступательное движение вдоль силовой линии и движение по окружности. Вектор скорости разложим на две составляющие: параллельную и перпендикулярную вектору магнитной индукции:

,

где ₁₁ =  соs, _ =  sin. Модуль вектора скорости .

На заряженную частицу (в данном случае протон) в магнитном поле действует сила Лоренца F_лор = QBsin.

По второму закону Ньютона

.

Сила Лоренца перпендикулярна вектору скорости и направлена к центру окружности, которую описывает протон в магнитном поле.

, т.е .

Следовательно, .

Шаг винтовой траектории h = ₁₁T,

где  период вращения протона. Учитывая, что радиус траектории , найдем параллельную составляющую скорости

.

Скорость протона равна

.

м/с.

Ответ:  = 2,410⁶ м/с.

Задача 4. В области пространства созданы электрическое поле с напряженностью Е = 10⁴ В/м и магнитное поле с индукцией В = 0,4 Тл. Векторы напряженности электрического поля и индукция магнитного поля взаимно перпендикулярны. В каком направлении и с какой скоростью должна двигаться -частица, чтобы ее движение было равномерным и прямолинейным.

Решение.

На -частицу в электрическом поле действует сила , ( независимо от направления движения -частицы). В магнитном поле на -частицу действует сила Лоренца , ( , ). Для равномерного и прямолинейного движения -частицы необходимо выполнение условия: . Это условие выполняется, если силы противоположно направлены и равны по модулю: QE = QBsin. Магнитная сила будет направлена противоположно электрической (по рисунку вниз), если частица движется перпендикулярно силовым линиям магнитного поля, т.е  = 90⁰, sin = 1.

Скорость -частицы

 = E/B.

 = 10⁴/0,4 = 2,510³ м/с.

Ответ:  =2,510³ м/с.