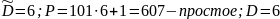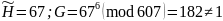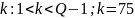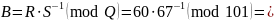Генерация сильно простого числа и порождающего элемента.

На практике простые числа, используемые в качестве параметров системы должны обладать следующим свойством:

где Q – достаточно большое простое число (более 160 бит в двоичном представлении), а – случайное (произвольное последовательным перебором) натуральное четное число, длина двоичного представления которого обеспечивает необходимую длину числа P. Такие числа P называют сильно простыми. Для вычислений по модулю таких чисел трудно организовать факторизацию и дискретное логарифмирование.

Кроме того на практике порождающий (примитивный элемент конечного поля) легко вычисляется при помощи подбора случайного (произвольного) натурального числа 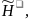как [10]:

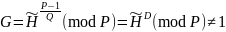
Проверку правильности подбора осуществляют вычислением:

Случай, когда G^Q отлично от 1, означает ослабление алгоритма в G^Q раз.

Задача 4.2’. Решить задачу 4.2 с вычислением примитивного элемента G, вместо назначения G_min при помощи шаблона электронной таблицы.

Комментарий к задаче.

Для вычисления G необходимо разложить число (P - 1) на простые множители. За Q принять наибольший простой делитель (P - 1). Далее подбирается произвольное до тех пор, пока не будет выполнено условие:

Кроме того, возможен также произвольный подбор G с последующей проверкой условия

.

Задача 4.3. По заданному простому числу Q осуществить генерацию сильно простого числа P ≤ 1000, пользуясь таблицей простых чисел (см. Приложение 1). Затем сгенерировать порождающий элемент G.

Пример решения.

Дано: Q = 101	Решение:
Найти: P, G Проверить: по GQ = 1
Проверка:

Цифровая подпись dsa.

Данная система является дальнейшим развитием схемы Эль-Гамаля. Главное достоинство системы в том, что использование в качестве модуля сильно простого числа позволяет ряд вычислений производить по модулю порядка циклической мультипликативной подгруппы Q. Данное обстоятельство снижает потребную вычислительную мощность и позволяет также сильно уменьшить размер собственно подписи (с 2 по 1024 до 2 по 160 бит). Стойкость же подписи остается на уровне 1024 числа P.

Cистема использует общие для всех абонентов параметры: P, Q и примитивный элемент G.

Каждый абонент системы генерирует секретный ключ

Открытый ключ Y вычисляют как:

Абонент, желающий подписать сообщение M, выбирает сеансовый ключ дополнительных требований к k не выдвигается, так как Q – простое число.

Подпись представляет собой пару:

- первая часть подписи, не зависящая от подписываемого сообщения. R служит для неявной передачи эфемерного ключа и, ввиду независимости от подписываемого сообщения, может быть выработано заранее в фоновом режиме.

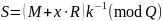- вторая часть подписи, связанная с сообщением M.

Для проверки подписи необходимо вычислить два промежуточных параметра:

Подпись считается верной при выполнении равенства:

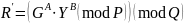
Данная схема стала основой стандарта цифровой подписи DSS.

Задача 4.4. Для заданного сильно простого числа P и соответствующего простого числа Q, открытого текста M и порождающего элемента G, самостоятельно определить остальные параметры схемы электронно-цифровой подписи DSA и осуществить подписание сообщения. Проверить правильность цифровой подписи.

Пример решения.

Дано: Q = 101 P = 607 G = 182 M = 45	Решение:
Найти: x, Y, k, R, S, A, B Проверить: R’ = R
Проверка: Задача 4.4’. Решить задачу 4.4 с самостоятельным нахождением по данному Q сильно простого числа P и порождающего элемента G.