1.4.1. Поділ кола на рівні відрізки

Поділ кола на чотири рівні частини (рис. 37, а). Два взаємно перпендикулярних діаметри ділять коло на чотири рівні частини. Сполучаючи точки поділу, отримують вписаний квадрат.

Поділ кола на вісім рівних частин (рис. 37, б). Дуги між точками А і С, В і С ділять навпіл за допомогою циркуля або транспортира. Точки поділу сполучають з центром кола і продовжують прямі до перетинку з протилежною половиною кола. Сполучаючи точки поділу, отримують правильний вписаний восьмикутник.

Поділ кола на три рівні частини (рис. 37, в). З точки D кінця вертикального діаметра, як із центра, радіусом кола проводять дугу, що перетинає коло в точках М і N. Сполучаючи точки M, N та С, отримують правильний вписаний трикутник.

П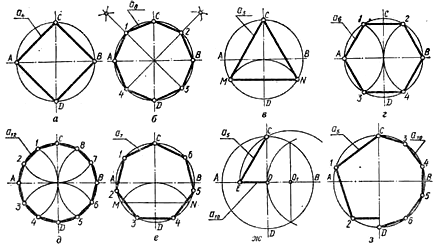 оділ кола на шість рівних частин (рис. 37, г). З кінців А і В горизонтального діаметра радіусом кола проводять дуги, що перетинають коло в точках 1, 2, 3 і 4. Сполучаючи точки поділу між собою і з А і В, отримують правильний вписаний шестикутник.

Рисунок 37. Поділ відрізка на рівні частини.

Поділ кола на сім рівних частин (рис. 37, е). Розділивши коло на три рівні частини, отримують хорду MN — сторону правильного вписаного трикутника. Половина цієї хорди із достатнім наближенням дорівнює стороні вписаного семикутника.

Поділ кола на п’ять та десять рівних частин (рис. 37, ж, з). Радіус кола ОВ ділять на дві рівні частини і, приймаючи точку О₁ за центр, проводять дугу радіусом, рівним відрізку О₁С. Ця дуга перетинає горизонтальний діаметр кола в точці Е. Відрізок ЕС дає величину сторони правильного вписаного п'ятикутника, а відрізок ЕО приблизно дорівнює стороні вписаного десятикутника. На рис. 37, з зображені половини вписаного п’ятикутника і десятикутника.

1.4.2. Побудова аксонометричних проекцій плоских фігур

Залежно від положення координатних осей відносно площини аксонометричних проекцій, утворюються різні аксонометричні проекції. Вони поділяються на ізометрію, прямокутну та косокутну диметрію.

Для побудови аксонометричних проекцій розміри зображень відкладають вздовж осей х, у, z. Тому побудову аксонометричної проекції починають з проведення ксонометричнох осей.

Положення осей ізометричної проекції (рис. 38, а): вісь z проводять вертикально, а осі х і у – під кутом 30° до горизонтальної лінії (120° між осями). Для побудови зображення відкладають натуральні розміри предмета.

Осі прямокутної диметричної проекції розміщують, як показано на рис. 38, б: вісь х – горизонтально, вісь z – вертикально, вісь у – під кутом 45° до горизонтальної лінії. Для побудови зображення вздовж осей х і z (і паралельно їм) відкладають натуральні розміри предмета, по осі у (і паралельно їй) – розміри зменшені вдвоє.

Осі косокутної симетричної проекції (рис. 38, в) проводять: z – вертикально, у – під кутом 41°, а х – під кутом 7° до горизонтальної лінії. Розміри предмета вздовж осей відкладають, як в прямокутній диметрії.

а б в

Рисунок 38. Розташування осей в аксонометричних проекціях

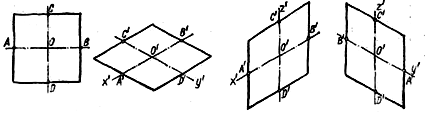
На рис. 39, а в ізометрії накреслено квадрат. Щоб побудувати квадрат, що лежить в площині П₁, проводять осі О'x' і О'у' та відкладають на осях від точки О' відрізки О'А', О'В', О'С', О'Д', що дорівнюють половині сторони квадрата. Через отримані точки А', В', С', D проводять прямі, паралельні аксонометричним осям. Квадрат в ізометрії зображують у формі ромба. Справа на рис. 39 зображені квадрати, що лежать в площинах П₂ та П₃.

а б в г

Рисунок. 39. Побудова квадрата в ізометрії

На рис. 40 накреслений шестикутник в ізометрії. Діагональ AD дорівнює подвійній величині сторони шестикутника. На ізометричних осях відкладають по обидві сторони від точки О' величину сторони шестикутника. На осі О'у' знаходять точку 4´, симетрично до неї на осі О´у´ визначаємо точку 4₁´. Через точки 4´ та 4₁´ проводять прямі, паралельні осі О´х´, а через точки N´ та N₁´ (середини відрізків О´А´ і О´D´) – прямі, паралельні осі О´у´. Взаємний їх перетин дає вершини шестикутника В´, С´, Е´, F´.

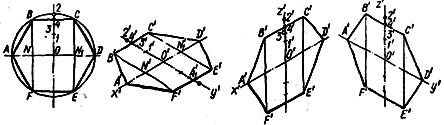
Рисунок 40. Шестикутник в ізометрії

На рис. 41, 42 в прямокутній диметрії зображено трикутник та п’ятикутник. Розглянемо побудову п’ятикутника, якщо задана сторона АВ (рис. 42). Проводимо взаємно перпендикулярні координатні осі Ох та Оу. На осі Ох відкладають відрізок МN, який дорівнює величині сторони п’ятикутника (МN = АВ). На осі Оу відкладають відрізок ОТ = ОМ/2, а на осі Ох вліво і вправо від точок М і N – відрізки МС₀ = ND₀ = 1/3МN. З точок С₀ та D₀ проводять прямі, паралельні осі Оу, а з точки Т – пряму, паралельно Ох. Взаємний їх перетин дає вершини п’ятикутника С і D. На осі Оу відкладають відрізок ОК = 2/3 МN та через точку К проводять пряму, паралельну осі Ох, на якій відкладають величину АВ сторони п’ятикутника. Для побудови вершини Е відкладають відрізок КЕ, що дорівнює 3АК. З’єднуючи точки А, В, D, Е, С, отримують п’ятикутник в симетрії, з урахуванням показника спотворення по осі О´у´ (0,5).

Рисунок 41

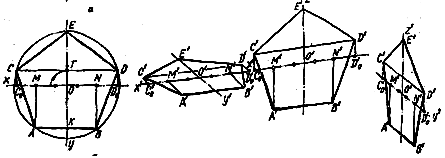
Рисунок 42

Коло в аксонометричній проекції зображають у вигляді еліпса, але на практиці прийнято заміняти їх на овали.

Розглянемо два способи побудови чотирицентрового овалу, що наближено замінює ізометричну проекцію кола, розташовану в площині проекцій або їй паралельній. Припустимо, що потрібно побудувати ізометричну проекцію кола діаметром 60 мм,, розташовану в площині проекцій П₁

1-й спосіб (рис. 43, а – в). Проводять ізометричні: осі О'x' і О'у та відкладають на них в обидві сторони від точкі О' відрізки, що дорівнюють радіусу заданого кола, тобто 30 мм. Через знайдені точки 1' 2' 3' 4' проводять прямі, паралельні аксонометричним осям, і отримують ромб A'B'C'D', що являє собою ізометрію квадрата, описаного навколо кола. Вершини ромба А' і С', що лежать на короткій діагоналі, є центрами великих дуг овала. Сполучають променямии точку А' з точками 2' і 3' і в перетині з великою діагоналлю B'D' ромба отримують ще два центри дуг овала О'₁ і О'₂. З центрів А' і С' проводять дуги радіусом R₁ = А'2', а з центрів O'1 і O'2 малі дуги радіусом R2 = О'₂3'. Hа рис. 43, г цим же способом побудована ізометрична проекція кола, що лежить в площині проекцій П₂, а на рис. 43, д—ізометрична проекція кола, що лежить в площині П₃.

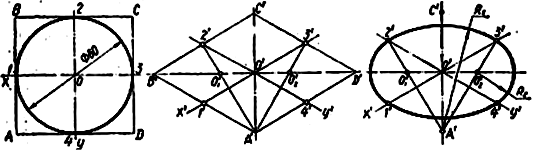
а б в

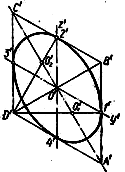
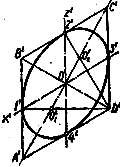
г д

Рисунок 43. Побудова кола в ізометрії (1 спосіб)

2-й спосіб. Визначають розміри великої і малої осей еліпса: А' В' = l,22d = 1,22× 60 = 73,2 мм; C'D' = 0,7d = 0,7×60 = 42 мм.

Через точку О' початок аксонометричних осей проводять дві взаємно перпендикулярні прямі (рис. 44 а, б). З точки О', як з центру, проводять кола, діаметри яких відповідно дорівнюють великій і малій осям еліпса, тобто l,22d і 0,71d. На вертикальному у діаметрі великого кола відзначають центри О'₁ і O'₂, а на горизонтальному діаметрі малої центри О'₃ і O'₄. Вони є центрами сполучення дуг овала. Проводять прямі О'₁О'₃; O'₁O'₄; О'₂О'₃; O'₂O'₄, на яких розташовані точки сполучення дуг овалу. Дві дуги радіуса R₁ = O'₂C|' описують з центрів O'₁ і O'₂,, а два інші радіуси R₂ = O'₄В' з центрів O'₃ і O'₄.

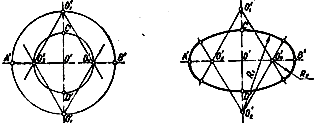
Рисунок 44. Побудова кола в ізометрії (2 спосіб)

Побудова кола в диметрії. На рис. 45, зображена диметрична проекція куба із вписаними в його грані колами. Передня і задня грані куба проектуються у вигляді ромбів, а інші грані – у вигляді паралелограмів. Кола проеціюються у вигляді еліпсів, малі осі яких, як і в ізометрії, паралельні осям, відсутнім в площинах даних кіл (напрям малих осей вказано потовщеною лінією). Наприклад, для еліпса, що лежить в горизонтальній площині, мала вісь йде за напрямом осі OZ, а велика – перпендикулярно до неї.

Довжина великої осі для всіх еліпсів однакова і дорівнює 1,06 діаметра зображеного кола (l,06d). Величина малої осі різна: для передньої і задньої граней куба, тобто для фронтальної площини проекцій, величина малої осі дорівнює 0,9 довжин великої осі, або 0,95 діаметра кола (0,95d); для верхньої і лівої граней куба і для площин, паралельних їм, величина малої осі дорівнює 1/3 великій осі, тобто 0,35 діаметра кола (0,35d). На рис. 45, г побудований графік, за допомогою якого можна визначити розміри великої і малої осей еліпса для довільного діаметра кола.

Розглянемо побудову овала, що лежить в площинах П₁ або П₃ (рис. 45 б,в). Через точку О' початок аксонометричних осей проводять дві взаємно перпендикулярні прямі і відкладають на горизонтальній прямій величину великої осі А'В' = l,06d, а на вертикальній – величину малої осі CD' = 0,35d. Вгору і вниз від точки О по вертикалі відкладають відрізки О'О'1