Розрахункова робота №3 нелінійні економетричні моделі Хід роботи

1. Побудувати такі види нелінійних економетричних моделей: експоненційну, степеневу і зворотну.

2. Розрахувати значення параметрів моделей.

3. Здійснити перевірку моделей на адекватність та оцінити тісноту зв’язку.

4. Здійснити вибір моделі, яка краще описує залежність і обґрунтувати.

5. Розрахувати точковий та інтервальний прогноз значення показника У для останнього значення фактора Хр за обраною моделлю.

Теоретичні відомості

Якщо між економічними явищами існують нелінійні співвідношення, то вони виражаються за допомогою відповідних нелінійних функцій.

Наприклад, нелінійними виявляються виробничі функції (залежності між обсягом виготовленої продукції і основними факторами виробництва - працею, капіталом і т.п.), функції попиту (залежність між попитом на товари або послуги і їхні ціни, або доходом) та інше.

Для оцінки параметрів нелінійних моделей використовують два підходи. Перший підхід заснований на лінеаризації моделі і полягає в тому, що за допомогою перетворень вихідних змінних залежність, яку досліджують, представляють у вигляді лінійного співвідношення між перетвореними змінними.

Другий підхід звичайно застосовують у випадку, коли підібрати відповідне перетворення, що лінеаризує, не вдається. В цьому випадку застосовують методи нелінійної оптимізації на основі вихідних змінних. Для лінеаризації моделі в рамках першого підходу можуть використовуватися як моделі, нелінійні за змінними, так і нелінійні за параметрами. Якщо модель нелінійна за змінними, то введенням нових змінних її можна звести до лінійної моделі, для оцінки параметрів якої використати звичайний метод найменших квадратів. Треба, однак, відзначити й недолік такої заміни змінних, пов'язаний з тим, що оцінки параметрів виходять не з умови мінімізації суми квадратів відхилень для вихідних змінних, а з умови мінімізації суми квадратів відхилень для перетворених змінних, що не те саме. У зв'язку із цим необхідне певне уточнення отриманих оцінок.

Економічна практика вже накопичила певний досвід і певні типи кривих, які найчастіше використовуються в макро- та мікроекономічних дослідженнях. До таких кривих відносяться:

експоненційна ; (3.1)

степенева (мультиплікативна) ; (3.2)

зворотна . (3.3)

(3.1)

(3.2)

(3.3)

У загальному випадку однофакторну економетричну модель можна подати у вигляді:

У = f(x) + Ɛ, (3.4)

де f(x) — одна з функцій зростання;

Ɛ — випадкова величина.

Як і у випадку з простою лінійною регресією, основне завдання полягає в розрахунку невідомих параметрів кривих зростання і подальшому аналізі обраної моделі. Оцінку невідомих параметрів проводять по-різному: експоненційні функції шляхом логарифмічних перетворень зводять до лінійної регресії, квадратичні функції зводять до багатофакторної регресії, для інших використовують ітеративні методи, метод трьох точок, метод Тейла тощо. Розглянемо функції зростання, які шля­хом перетворень зводяться до лінійної регресії. Для таких функцій збері­гається вся методологія досліджень, яка була детально розглянута у випадку простої лінійної регресії.

Експоненційна функція

Експоненційна функція може набирати різних чисельних еквівалентних форм, розглянемо одну з них:

. (3.5)

Звичайно, перед нами постає запитання: як можна розрахувати невідомі параметри експоненційної кривої? Покажемо, що шляхом логарифмічно­го перетворення можна легко звести експоненційну криву до лінійної функції, що дає змогу розраховувати параметри мето­дом найменших квадратів та використовувати подальший аналіз моделі, як і в разі простої лінійної регресії. Отже, маємо:

ln(y)=b₀+b₁x,

y₁= b₀+b₁x.

Проводячи необхідну заміну змінних, переходимо до моделі лінійної регресії, розрахунок параметрів та всі необхідні дослідження якої розглянуто у розрахунковій роботі №2.

Cтепенева (мультиплікативна) функція

Степенева функція є однією з найпоширеніших у практиці кривих зростання і описує дуже широкий спектр економічних процесів. Вона має такий вигляд:

у = x^. (3.6)

Ми розглядатимемо випадок, коли параметр ≥0, що є типовим для економічних процесів. Якщо значення параметра  — не ціле число, то розглядають лише випадок, коли x≥0. При цьому залежно від знака параметра  степенева функція описуватиме різні економічні процеси: прискорене зростання, уповільнене зростання та спад. Слід зазначити, що якщо =1, степенева функція перетворюється на лінійну. Ці різні ситу­ації зображені на рисунку 3.1 (а, б, в, г).

Якщо параметр  степеневої функції — ціле число, то залежно від того, парне чи непарне його значення, графік функції має різний вигляд. Якщо  — парне, тобто його можна записати у вигляді: =2k, k ε Z (розгляне­мо тільки випадок, коли k>0), тоді y є [0,+), а графік функції симетрич­ний відносно осі ординат (рисунок 3.2, а).

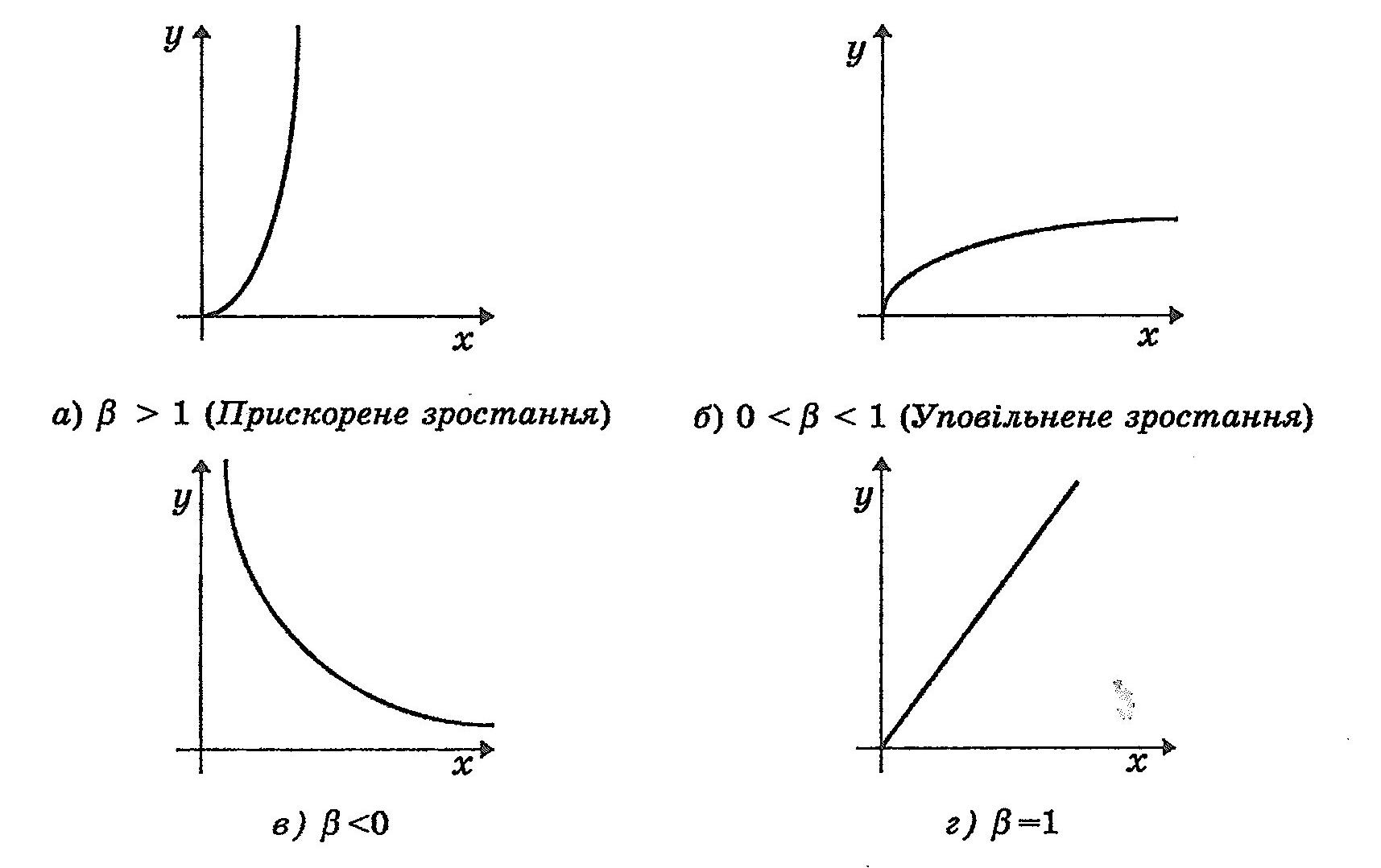
Рисунок 3.1 - Вигляд степеневої функції, коли  - не ціле число, х≥0

Якщо параметр  — непарне число, тобто його можна подати у вигля­ді: =2k-1, k ε Z₊ (розглянемо тільки випадок, коли k>0), тоді у є R, а графік функції симетричний відносно початку координат (0,0) (рис. 3.2, б).

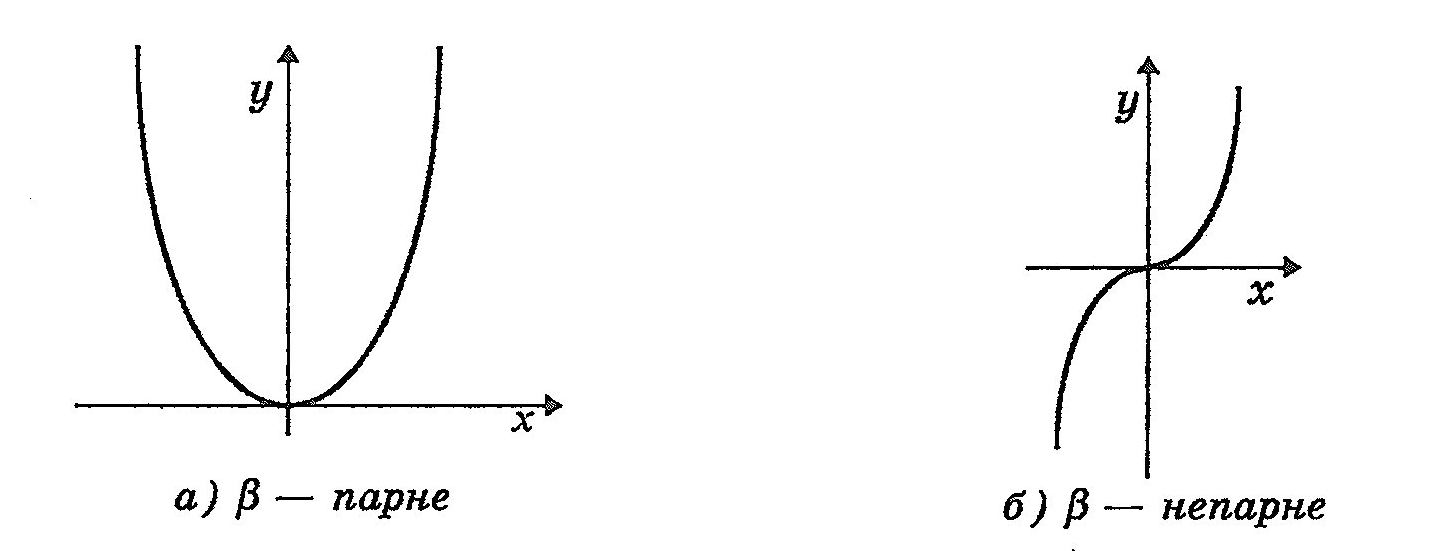
Рисунок 3.2 - Графік степеневої функції, коли b – ціле число

Звичайно, основне питання полягає в тому, щоб розрахувати невідомі параметри мультиплікативної (степеневої) кривої. Покажемо, що шля­хом логарифмічного перетворення ми можемо легко звести степеневу криву так само, як і експоненційну, до лінійної функції, що дає нам змогу розра­ховувати параметри методом найменших квадратів. Справді, логарифму­ючи праву та ліву частини (3.6), отримаємо:

,

.

На практиці степеневі функції використовуються для опису різних еко­номічних процесів. Найвідомішою з них є виробнича функція Кобба-Дугласа. Крім того, вони застосовуються для опису кривих байдужості, а також попиту на товари різних категорій, так звана крива Торнквіста та ін.

Зворотна функція

Узагальнена зворотна модель має вигляд:

(3.7)

Вона нелінійна за змінною х, але лінійна за параметрами ₀ і ₁, і тому є лінійною регресійною моделлю.

Справді, позначивши 1/x_i=z_i отримаємо:

(3.8)

Вибіркова зворотна модель, враховуючи позначення попереднього розділу, може бути записана у вигляді:

(3.9)

де b₀ та b₁ — невідомі параметри, які необхідно знайти; е — помилка.

Модель має свої особливості, на відміну від простої лінійної регресії: коли х прямує до нескінченності, величина b₁(1/x_i) прямує до нуля, а у прямує до граничного значення.

Вигляд моделі (3.9) значною мірою залежить від знака параметрів b₀ і b₁.

Нахил моделі (3.9) визначаємо за такою формулою:

(3.10)

Він є додатним, коли b₁ < 0, і від'ємним, коли b₁ > 0.

Вибір найкращого рівняння у випадку, якщо економетрична модель є нелінійною, можна здійснити шляхом розрахунку за кожним рівнянням коефіцієнта детермінації R² і вибору залежності з максимальним його значенням.