Питання для самоперевірки
1 У чому полягає метод середньої ковзання?
2 Поясність суть методу простої експоненціально-зваженої середньої.
3 Які показники використовують для оцінки точності прогнозу?
4 Назвіть показники для оцінки зміщеності прогнозу.
5 Для чого використовують коефіцієнт Трігга?
Тестові завдання
1 Формула Брауна використовується для:
а) розрахунку прогнозу методом середньої ковзання;
б) розрахунку прогнозу методом ПЕВС;
в) розрахунку прогнозу за допомогою тренду;
г) оцінки точності прогнозу.
2 Середній квадрат похибки розраховують для:
а) перевірки достовірності пронозу;
б) перевірки точності прогнозу;
в) перевірки зміщеності прогнозу;
г) визначення прогнозного значення показника.
3 Прогноз вважається незміщеним, якщо:
а) |СПП| < 5%;
б) |СПП| > 5%;
в) |СПП| > 50%;
г) розрахункове значення коефіцієнту Трігга більше табличного.
4 Якщо розрахункове значення коефіцієнту Трігга більше табличного, то прогноз вважається:
а) недостовірним;
б) зміщеним;
в) точним;
в) достовірним.
Вихідні дані для виконання розрахункової роботи №7 обираємо згідно варіанту з таблиці 7.3.
Таблиця 7.3 – Вихідні дані до розрахункової роботи №7
Варіант |
Числові значення показника |
|||||||||
1 |
8,15 |
7,24 |
6,31 |
6,24 |
5,47 |
4,53 |
3,67 |
3,08 |
2,44 |
1, 81 |
2 |
8,71 |
7,64 |
6,9 |
6,28 |
6,28 |
4,55 |
3,94 |
3,3 |
3,23 |
2,15 |
3 |
7,76 |
6,83 |
6,02 |
6,06 |
5,02 |
4,18 |
3,67 |
2,85 |
2,12 |
1,77 |
4 |
10 |
8,12 |
6,68 |
7,7 |
5,64 |
6,33 |
3,93 |
4,46 |
2,64 |
2,26 |
5 |
8,33 |
8,96 |
8,06 |
6,34 |
7,08 |
5,64 |
4,85 |
4,06 |
2,94 |
2,9 |
6 |
7,6 |
6,7 |
5,79 |
6,08 |
5,37 |
3,71 |
2,68 |
2,36 |
2,13 |
1,48 |
7 |
9,04 |
7,24 |
6,55 |
6,88 |
6,15 |
4,55 |
3,97 |
3,58 |
3,08 |
1,93 |
8 |
9,18 |
7,79 |
7,2 |
6,52 |
5,74 |
4,61 |
3,83 |
3,38 |
3,23 |
2,33 |
9 |
8,39 |
7,37 |
6,6 |
6,44 |
5,5 |
4,75 |
3,9 |
3,26 |
2,51 |
2,03 |
10 |
8,05 |
6,66 |
6,14 |
5,21 |
4,85 |
3,91 |
3,21 |
2,17 |
1,92 |
1,35 |
11 |
8,21 |
7,41 |
6,36 |
6,74 |
5,71 |
4,82 |
3,94 |
3,52 |
2,85 |
2,21 |
12 |
8,74 |
7,85 |
693 |
6,57 |
6,35 |
4,59 |
4,2 |
3,35 |
3,69 |
2,57 |
13 |
7,81 |
6,88 |
6,07 |
6,34 |
5,51 |
4,36 |
3,68 |
2,91 |
2,16 |
2,08 |
14 |
10,49 |
8,41 |
6,95 |
7,77 |
5,89 |
6,68 |
3,99 |
4,52 |
2,98 |
2,54 |
15 |
8,42 |
9,12 |
847 |
6,39 |
7,19 |
6,04 |
5,11 |
4,13 |
3,18 |
3,31 |
16 |
8 |
6,76 |
5,98 |
6,13 |
5,76 |
3,93 |
3,18 |
2,79 |
2,48 |
1,91 |
17 |
9,5 |
7,42 |
6,9 |
6,94 |
6,19 |
5,01 |
4,76 |
3,72 |
3,19 |
2,23 |
18 |
9,4 |
8,02 |
7,36 |
6,58 |
5,89 |
4,96 |
3,99 |
3,4 |
3,72 |
2,8 |
19 |
8,81 |
7,56 |
6,71 |
6,64 |
5,97 |
5,2 |
4,22 |
3,35 |
2,83 |
2,08 |
20 |
8,16 |
6,76 |
6,55 |
5,66 |
5,18 |
3,93 |
3,59 |
2,61 |
2,13 |
1,62 |
21 |
8,04 |
7,18 |
5,85 |
6,01 |
5,08 |
4,22 |
3,3 |
2,85 |
2,13 |
1,55 |
22 |
8,71 |
7,53 |
6,53 |
6,11 |
6,15 |
4,25 |
3,73 |
3,01 |
3,11 |
1,79 |
23 |
7,64 |
6,38 |
6,01 |
5,85 |
4,66 |
3,77 |
3,62 |
2,79 |
1,94 |
1,73 |
24 |
9,8 |
7,82 |
6,31 |
7,68 |
5,47 |
6,29 |
3,69 |
4,35 |
2,24 |
2,11 |
25 |
7,92 |
8,59 |
7,69 |
6,26 |
7,07 |
5,23 |
4,57 |
3,61 |
2,44 |
2,73 |
26 |
7,22 |
6,49 |
5,49 |
5,69 |
5,08 |
3,26 |
2,28 |
2,17 |
1,91 |
1,33 |
27 |
9,03 |
7,08 |
6,35 |
6,64 |
5,78 |
4,05 |
3,71 |
3,22 |
2,67 |
1,78 |
28 |
8,91 |
7,33 |
7,03 |
6,5 |
5,63 |
4,46 |
3,75 |
3,02 |
2,85 |
1,86 |
29 |
8,23 |
7,37 |
6,4 |
6,36 |
5,49 |
4,58 |
3,63 |
3,1 |
2,45 |
1,74 |
30 |
7,94 |
6,17 |
5,88 |
4,72 |
4,73 |
3,7 |
2,95 |
1,91 |
1,82 |
0,92 |
РОЗРАХУНКОВА РОБОТА №8
МОДЕЛЮВАННЯ СЕЗОННИХ КОЛИВАНЬ ЕКОНОМІЧНИХ ЯВИЩ РЯДАМИ ФУР’Є
Хід роботи
1 На основі вихідних даних описати сезонні коливання показника рядами Фур’є
2 Розрахувати прогнозне значення показника, побудувати графік.
3 Розрахувати показники точності і зміщеності прогнозу (СКП, СрКП, СПП, САПП), зробити відповідні висновки.
4 Вибрати гармоніку, яка найбільш адекватно описує ці сезонні коливання.
Теоретичні відомості
Значна частина економічних явищ, таких як попит на товари та послуги, пасажиропотоки, виробництво в цукровій та консервній промисловості носить сезонний характер.
Для аналізу та прогнозування таких сезонних явищ використовують ряд Фур’є, який представляє сезонне явище у вигляді гармоніки.
У загальному вигляді ряд Фур’є можна записати так:
,
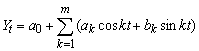(8.1)
де
,
,
–
параметри моделі,
t – фактор часу,
k – порядковий номер гармоніки,
m – кількість гармонік.
В економетричних дослідженнях кількість гармонік ряду Фур’є приймають не більшою 4, а потім визначають, яка із гармонік найбільш адекватно описує сезонні коливання економічних явищ.
Параметри
ряду Фур’є
,
,
визначаються
методом найменших квадратів. Формули
для розрахунку цих параметрів мають
вигляд:
,
(8.2)
,
(8.3)
.
(8.4)
де n – кількість періодів часу, за які розглядається явище (місяців, днів, кварталів, років).
Для побудови економетричної моделі необхідно зробити перехід для фактора часу від натурального масштабу до радіанного або градусного. Цей перехід можна здійснити за формулою:
,
(8.5)
де n – кількість спостережень (або кількість інтервалів часу, за який аналізується сезонне явище), ti – фактор часу у радіанному (градусному) вираженні, t’ – натуральний ряд чисел від 0 до n-1 (0,1,2, …, n-1).
Запишемо місяці у радіанній формі (таблиця 8.1).
Таблиця 8.1 - Радіанна форма місяців
січень |
0 |
|
липень |
|
лютий |
|
|
серпень |
|
березень |
|
|
вересень |
|
квітень |
|
|
жовтень |
|
травень |
|
|
листопад |
|
червень |
|
|
грудень |
|
Для визначення параметрів моделі та необхідно скласти таблицю значень тригонометричних функцій cost, cos2t, …, sint, sin2t, … (табл. 8.2).
Таблиця 8.2 - Значення тригонометричних функцій
|
, рад. |
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
2 |
|
0,866 |
0,5 |
0,5 |
0,866 |
3 |
|
0,5 |
-0,5 |
0,866 |
0,866 |
4 |
|
0 |
-1 |
1 |
0 |
5 |
|
-0,5 |
-0,5 |
0,866 |
-0,866 |
6 |
|
-0,866 |
0,5 |
0,5 |
-0,866 |
7 |
|
-1 |
1 |
0 |
0 |
8 |
|
-0,866 |
0,5 |
-0,5 |
0,866 |
9 |
|
-0,5 |
-0,5 |
-0,866 |
0,866 |
10 |
|
0 |
-1 |
-1 |
0 |
11 |
|
0,5 |
-0,5 |
-0,866 |
-0,866 |
12 |
|
0,866 |
0,5 |
-0,5 |
-0,866 |
Для оцінки якості прогнозу використовуються показники, наведені у розрахунковій роботі №7.