Розрахункова робота №5 тема: дослідження лінійної багатофакторної регресії Хід роботи

1. На основі вихідних даних, використовуючи функції програми Excel, визначити значення параметрів багатофакторної регресії.

2. Перевірити знайдену модель на адекватність вихідним даним.

3. Перевірити знайдені параметри на значущість.

4. Розрахувати та пояснити довірчий інтервал для показника при довільно заданих значеннях факторів.

5. Перевірити фактори на мультиколінеарність.

6. Перевірити модель на автокореляцію.

Теоретичні відомості

Задана вибірка змінних Y, які входять в економетричну модель. Допустимо, що між показником Y і факторами Х₁, Х₂, ..., Х_m існує лінійна залежність:

. (5.1)

Оцінки параметрів лінійної багатофакторної регресії та інші коефіцієнти можна визначити, використовуючи функції програми Excel.

Для цього перш за все необхідно перевірити наявність пакету аналізу. В головному меню слід вибрати Сервис-Надстройки і включити пакет аналізу:

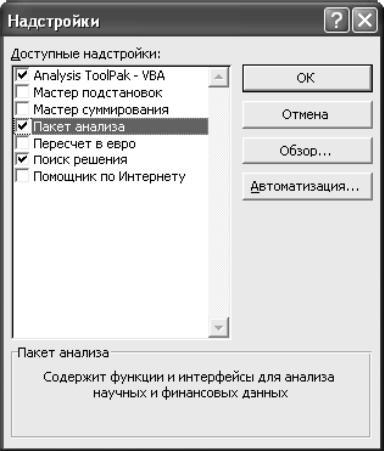
Рисунок 5.1 – Вибір пакету аналізу в MS Excel.

В головному меню вибираємо Сервис - Аналіз даних-Регресія. Отримуємо діалогове вікно (рис.5.2) та заповняємо його, попередньо ввівши вихідні дані показника та факторів для аналізованого періоду у чарунки MS Excel.

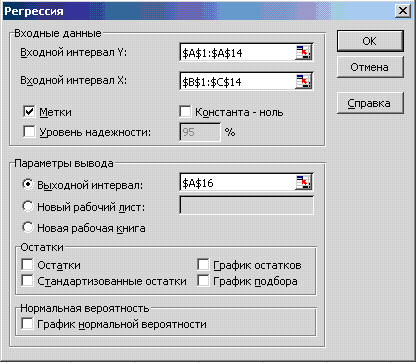
Рисунок 5.2 – Діалогове вікно

Таблиця 5.1 – Інтерпретація діалогового вікна

Входной интервал Y:	Діапазон значень залежної змінної.
Входной интервал X	Діапазон значень незалежних змінних. Зауважте, що незалежні змінні повинні знаходитися в сусідніх стовпчиках.
Метки	Опція, що вказує, чи містить перший рядок назви стовпчиків
Константа -ноль	Опція, що вказує на наявність чи відсутність константи в регресії
Параметри виводу	Адреса чарунки для виводу результатів обчислень. Якщо вказується опція «Новый рабочий лист», то результати виводяться на новий лист.

Для перевірки знайдених параметрів на значущість використовують критерій Ст’юдента. Для цього знаходимо емпіричне значення критерію за формулою:

, де (5.2)

Для формулювання висновку щодо значущості потрібно порівняти емпіричне значення критерію з табличним t_табл. Якщо t_емп > t_табл, то параметр регресії вважається статистично значущим з ймовірністю Р.

Мультиколеніарність

При побудові регресії, з одного боку, потрібно включати всі фактори, які мають значний статистичний вплив на показник, а з іншого боку, потрібно, щоб була виконана умова лінійної незалежності між факторами. Якщо існує лінійна залежність хоча б між двома факторами, то говорять, що між цими факторами існує мультиколінеарність. При визначенні лінійної структури корисно будувати кореляційну матрицю, в які включені фактори і показник. У регресію потрібно в першу чергу включати фактори, які корелюють з показником і не корелюють між собою. В економетричних задачах для дослідження наявності мультиколінеарності широко застосовується метод Феррара-Глобера.

Метод Феррара-Глобера

Цей метод містить три види статистичних критеріїв, на основі яких перевіряють мультиколінераність:

­–­ масиву незалежних змінних загалом (критерій );

• кожної незалежної змінної з усіма іншими (F-критерій);

• кожної пари незалежних змінних (t-критерій).

Для дослідження загальної мультиколінеарності і мультиколінеарності між окремими факторами використовується кореляційна матриця [R] і обернена до неї матриця [Z].

Для отримання кореляційної матриці необхідно пронормалізувати змінні Х₁, Х₂, ..., Х_m економетричної моделі, для чого обчислити:

, (5.3)

де n – кількість спостережень, (i=1,2,…, n),

m – кількість незалежних змінних, які входять у модель, (j=1,2,…, m).

, (5.4)

де [R] – кореляційна матриця;

[X^*] – матриця нормалізованих статистичних даних факторів;

[X^*]^T – транспонована матриця по відношенню до матриці [X^*].

Для дослідження загальної мультиколінеарності використовується критерій (хі-квадрат).

Для цього знаходиться визначник кореляційної матриці det[R] і знаходиться розрахункове значення критерію:

. (5.5)

За заданою ймовірністю Р і числом ступенів вільності знаходиться табличне значення . Порівнюють розрахункове і табличне значення .

Якщо , то із заданою надійністю можна вважати, що загальна мультиколінеарність відсутня і на цьому закінчується дослідження мультиколінеарності. Якщо > , то з прийнятою надійністю можна вважати, що між факторами існує мультиколінеарність. Для з’ясування питання, між якими факторами існує мультиколінеарність використовується F- або t-статистика.

Для знаходження F-критеріїв потрібно визначити матрицю Z-помилок:

[Z]=[R]^-1= . (5.6)

Відповідно розрахункове значення F-критерію:

(5.7)

де Z_kk – діагональні елементи матриці Z.

Значення критеріїв F_k порівнюють з табличним при (n-m) і (m-1) ступенях свободи і рівні значущості α (якщо F_k>F_табл, то відповідна k-та незалежна змінна мультиколінерна з іншими).

Для знаходження t-критеріїв потрібно знайти часткові коефіцієнти кореляції, які характеризують щільність зв’язку між двома змінними за умови, що всі інші змінні не впливають на цей зв’язок (існування парної мультиколінеарності):

(5.8)

де Z_kj – елементи матриці Z, що розміщують в k-му рядку та j-му стовпці, k=1,2,...,m; j=1,2,…,m; Z_kk, Z_jj – діагональні елементи матриці Z.

Відповідно розрахункове значення t-критерію:

. (5.9)

Значення критеріїв t_kj порівнюють з табличним при (m-n) ступенях свободи і рівні значущості α; якщо t_kj > t_табл, то між незалежними змінними Х_k і Х_j існує мультиколінеарність. На основі розрахованих критеріїв роблять висновок про виключення фактору з побудованої моделі (якщо F_k > F_табл або t_kj>t_табл).

Автокореляція

Одним із показників ступеня близькості одержаної лінії регресії до експериментальних даних є критерій Дарбіна-Уотсона. Він дає відповідь на запитання, чи є істотною автокореляція відхилень від лінії регресії. Іншими словами, з деякою надійністю критерій дає відповідь на запитання, чи виконується умова незалежності відхилень е_t.

Автокореляція відхилень – це кореляція відхилень від лінії регресії з відхиленнями від цієї лінії, взятими з деяким запізненням, тобто це кореляція ряду е₁,е₂, ..., е_n з рядом е_k+1, е_k+2, …, е_k+n, де k – число, що характеризує запізнення.

Кореляція між сусідніми членами ряду (k=1) називається автокореляцією першого порядку:

. (5.10)

Відповідно d-статистика може набувати будь-якого значення з інтервалу (0;4).

Для d-статистики визначені критичні межі (d_l – нижня, d_n – верхня), які дозволяють із заданою надійністю (Р=0,95; 0,99) дати відповідь, чи можна прийняти гіпотезу про відсутність автокореляції першого порядку чи ні.

У залежності від значення d приймаємо, що:

1. при 0<d<d_l відхилення додатно корельовані;

2. при d_n<d<4-d_n враховується гіпотеза про відсутність автокореляції;

3. при 4-d_l<d<4 відхилення від’ємно корельовані;

4. при d_l<d<d_n або 4-d_n<d<4-d_l критерій не дає відповідь на запитання про наявність або відсутність кореляції.

Відхилення додатно корельовані	?	Враховується гіпотеза про відсутність автокореляції	?	Відхилення від’ємно корельовані
0 dl		dn 4-dn		4-dl 4

Якщо d-статистика набуває значення з п.4, то для одержання відповіді про наявність автокореляції першого порядку необхідно збільшити число спостережень. Величини d_n i d_l для двох надійних ймовірностей Р=0,95 і Р=0,99 наведено в таблицях.

При наявності автокореляції відхилень потрібно з’ясувати можливі причини її появи. Можливі причини автокореляції:

1. у регресію не включений фактор, який має суттєву роль при дослідженні економічного явища.

2. вибраний вигляд стохастичної залежності не адекватний експериментальним даним.

3. при дослідженні явища числові дані отримані з великими похибками.