ЗМІСТ

№ п/п	Зміст	ст.
	Розрахункова робота №1. Динамічні ряди та їх характеристики	2
	Розрахункова робота №2. Лінійна регресія	12
	Розрахункова робота №3. Нелінійні економетричні моделі	21
	Розрахункова робота №4. Дослідження економетричних моделей, побудованих на основі поліномів	31
	Розрахункова робота №5. Дослідження лінійної багатофакторної регресії	41
	Розрахункова робота №6. Дослідження нелінійної багатофакторної моделі	54
	Розрахункова робота №7. Прогнозування показників за допомогою середніх	65
	Розрахункова робота №8. Моделювання сезонних коливань економічних явищ рядами Фур’є	73
	Розрахункова робота №9. Прогнозування показників за методом Холта	78
	Перелік використаних джерел	81

Розрахункова робота №1 динамічні ряди та їх характеристики Хід роботи

1 На основі вихідних даних динамічного ряду розрахувати та пояснити зміст:

а) абсолютний приріст (базисний і ланцюговий);

б) темп росту (базисний і ланцюговий);

в) темп приросту (базисний і ланцюговий);

г) абсолютне значення 1% приросту.

2 Описати середні характеристики динамічного ряду: середню арифметичну, середній абсолютний приріст, середній темп росту та приросту.

3 Розрахувати дисперсію, середнє квадратичне відхилення, коефіцієнт варіації та пояснити отримані значення.

Теоретичні відомості

Динамічним рядом називається послідовність спостережень за процесом або явищем у рівновіддалені проміжки часу.

Кожний ряд динаміки містить два елементи:

• параметр часу (значення часу);

• значення рівнів ряду, що відповідають параметрам часу.

В якості показника часу в рядах динаміки можуть використовуватися або певні моменти часу (дати), або окремі періоди часу (доба, місяць, квартал, рік і т. д.). У залежності від характеру параметру часу ряди динаміки поділяють на моментні та інтервальні.

В моментних рядах динаміки рівні характеризують значення показника на певні моменти часу. Наприклад, моментними є часові ряди цін на певні види товарів, ряди курсів акцій, рівні яких фіксують на певні дати, ряди чисельності населення або вартості основних фондів, так як значення рівнів цих рядів визначаються щорічно на одну й ту ж дату.

Інтервальні ряди динаміки характеризують розміри досліджуваного явища за певні проміжки - інтервали (періоди) часу, тобто місяць, квартал, рік і т.д. До таких показників відносяться обсяг виробленої продукції, фонд заробітної плати та інші.

Позначимо через x_i значення деякої ознаки економічного процесу або явища в і-й проміжок часу. Тоді, вимірюючи значення цієї ознаки в рівновід­далені проміжки часу, отримаємо інтервальний динамічний ряд: x₁, x₂..., x_i...x_n. Окремі значення ознаки, які відносяться до певних проміжків часу, ще називають рівнями динамічного ряду. Наприклад, x_i — це значення ознаки, що ви­вчається у і-й проміжок часу.

Аналіз рядів динаміки має за мету вивчення зміни явища за часом і встановлення його напряму, характеру цієї зміни і вияв закономірності розвитку.

На практиці для кількісної оцінки динаміки явищ широко застосовуються наступні основні аналітичні показники:

• абсолютний приріст;

• темп росту;

• темп приросту;

• абсолютне значення одного відсотка приросту.

Обчислення характеристик ґрунтується на порівнянні рівнів ряду. При порівнянні якогось певного рівня з попереднім (база порівняння змінна) отримані показники називають ланцюговими. Якщо всі рівні ряду динаміки порівнюють з одним і тим самим рівнем (база порівняння стала), то отримані показники називають базисними.

Рівень, який зіставляється, називається поточним, а рівень, з яким зіставляються інші рівні - базисним. За базу зіставлення приймають або попередній, або початковий рівень ряду динаміки. Якщо кожний наступний рівень зіставляють з попереднім, то дістають ланцюгові показники динаміки (щорічні). А якщо кожний наступний рівень зіставляють з рівнем, що взято за базу зіставлень, то показники називаються базисними.

Абсолютний приріст - показує на скільки одиниць в абсолютному виразі змінився рівень динамічного ряду того чи іншого періоду порівняно з попереднім чи початковим. Абсолютний приріст може бути як позитивним, так і негативним.

Абсолютний приріст називається ланцюговим, якщо кожен рівень ряду динаміки порівнюється з попереднім рівнем:

Δx_л = x_i - x_{i -1}. (1.1)

Якщо всі рівні ряду порівнюють з початковим, то такий абсолютний приріст називається базисним:

Δx_б = x_i - x_{1 ,} (1.2)

де х₁ – значення ознаки прийняте за базисний рівень.

Темп росту (Т_р) - це показник ряду динаміки, який показує у скільки разів змінився поточний рівень показника, що аналізується порівняно з рівнем попереднього, або базового періоду.

За ланцюговою схемою темп росту розраховується за формулою:

. (1.3)

За базисною схемою темп росту розраховується за формулою:

. (1.4)

Темп росту завжди є позитивною величиною і дозволяє відповісти на питання на скільки відсотків змінився рівень динамічного ряду. Якщо темп росту дорівнює 100 %, то змін за відповідний період не відбулось; якщо менше 100% – то значення рівня динамічного ряду за період знизилось; якщо більше 100% – то значення рівня динамічного ряду за період збільшилось.

Темп приросту (Т_пр.) показує на скільки відсотків збільшився або зменшився поточний рівень ряду динаміки.

Ланцюговий темп приросту розраховується за формулою:

. (1.5)

Базисний темп приросту розраховується за формулою:

(1.6)

Абсолютне значення 1 % приросту - це відношення щорічного приросту за певний період до щорічного темпу приросту за той самий період або поточний рівень поділити на 100:

. (1.7)

Середні характеристики динамічного ряду

Узагальненими характеристиками динамічного ряду є середня арифметична, середній абсолютний приріст, середній темп росту та приросту.

В інтервальному ряді з рівними інтервалами часу застосовують середню арифметичну просту, що розраховується за формулою:

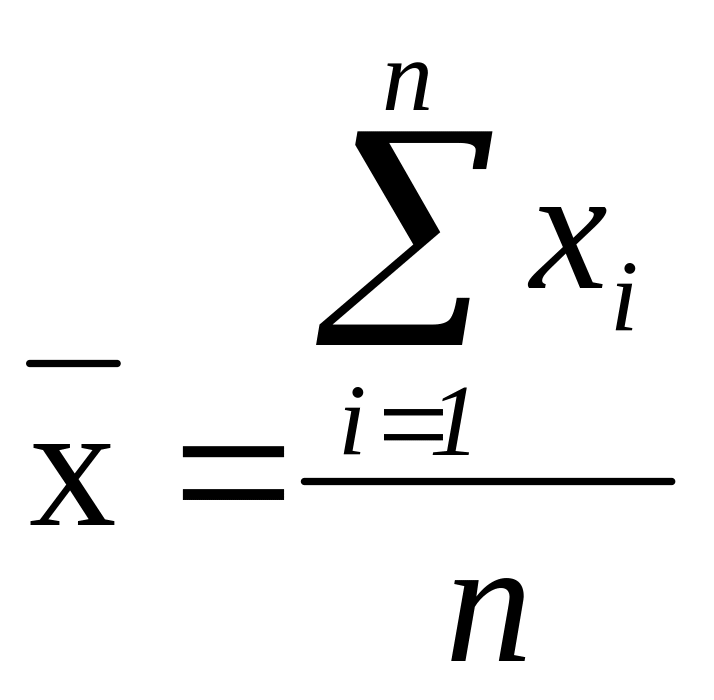, (1.8)

де x_i — і-й рівень динамічного ряду;

п — кількість спостережень (рівнів).

Середні арифметичні корисні для порівняльного аналізу двох або кількох динамічних рядів.

Середній абсолютний приріст показує, як швидко змінюється кінце­вий рівень ряду відносно початкового:

, (1.9)

де х_n, х₁ — кінцевий та початковий рівень ряду.

Середній темп росту характеризує середню швидкість зміни економічного процесу або явища і розраховується за формулою:

(1.10)

Середній темп приросту розраховується за формулою:

. (1.11)

Середніх характеристик часом буває недостатньо для характеристики рядів. Інколи два ряди мають однакові середні, але по різному можуть бути згруповані навколо середнього. В такому випадку для характеристики динамічних рядів використовують показники варіації (розсіювання).

Відхилення від середнього значення вимірює дещо штучна величина — дисперсія.

Дисперсія показує середню суму квадратів відхилень значень ознаки від свого середнього і позначається ², або var(x):

, (1.12)

де — середнє значення динамічного ряду;

n — кількість спостережень.

У підрахунках дисперсії використовується середня сума квадратів відхи­лень, тому що середня сума відхилень дорівнює нулеві. Справді:

.

Для того, щоб дисперсію можна було порівняти з середніми характеристи­ками, вводиться середнє квадратичне відхилення:

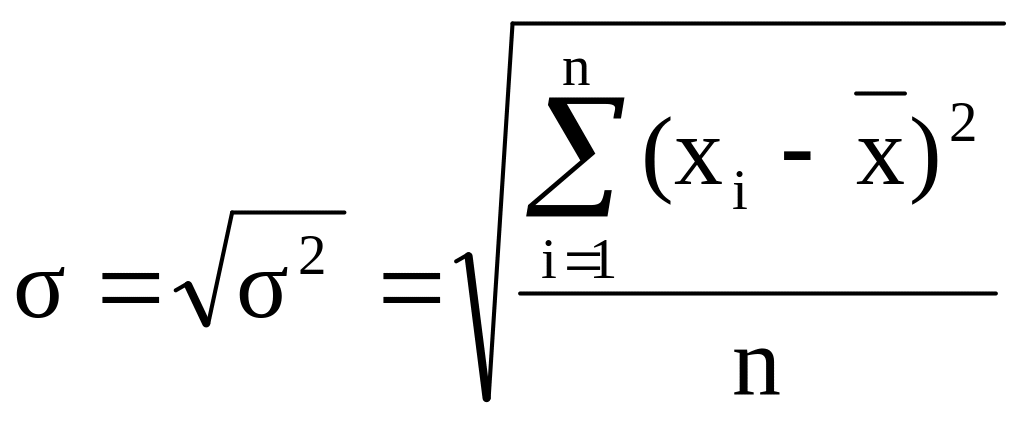. (1.13)

Середнє квадратичне відхилення показує на скільки в середньому відхиляються індивідуальні значення ознаки від їх середнього рівня.

Чим менше середнє квадратичне відхилення, тим краще середня арифметична відображає всю сукупність ознак динамічного ряду.

Дисперсія цікава також тим, що яким би не був розподіл величини х, як мінімум 75% спостережень знаходяться між (х - 2) та (x+2).

Для порівняння ступеня коливання значень ознаки різних динамічних рядів використовують відносний показник — коефіцієнт варіації, який являє собою відношення середнього квадратичного відхилення до середньої арифметичної, виражене у відсотках:

, (1.14)

де V — коефіцієнт варіації;

х — середнє значення ряду;

 - середнє квадра­тичне відхилення.

Коефіцієнт варіації вказує на відносну міру коливання ознаки навколо середньої величини

Коефіцієнт варіації дає змогу:

- порівняти варіацію однієї ознаки у різних групах об‘єктів;

- виявити ступінь відмінності однієї ознаки в одній групі об‘єктів за рівні проміжки часу;

- порівняти варіацію різних ознак в однакових групах об‘єктів.

Чим меншим є коефіцієнт варіації, тим меншими є коливання значень досліджування ознаки і навпаки. Якщо величина коефіцієнта варіації знаходиться в межах до 10%, то це свідчить про невелике коливання ознаки навколо середньої величини і вказує на якісну однорідність сукупності. Якщо величина коефіцієнта варіації знаходиться в межах від 11% до 25%, то варіація ознаки вважається середньою, а сукупність можна вважати майже однорідною, якщо ж коефіцієнт варіації перевищує 25%, то варіація є сильною, а сукупність неоднорідною.