
- •1. Алгоритмы сжатия изображений.
- •2 Аппаратное обеспечение мультимедиа.
- •3Виды и принцип действия cd-rom.
- •4 Виды памяти.
- •5Использование звука . Стандарты звуковых карт
- •6. Организация сетей для передачи мультимедиа-данных.
- •7 Синтезированные звуковые карты с частотной модуляцией.
- •8 Составляющие изображения, технология ускорения графики.
- •9 Способы передачи мультимедиа-данных в сетях.
- •10 Технология видеодисплеев
- •12 Организация виртуальной памяти.
- •13 Стратегии замещения и размещения страниц. Принцип локальности
- •14 Этапы загрузки операционных систем (Unix, Windows nt).
- •14. Этапы загрузки операционных систем (Unix, Windows nt).
- •15 Организация фс fat , основные элементы структуры.
- •16 Организация файловой системы fat32 отличия от fat16, преимущества.
- •17 Особенности организации файловой системы unix. Файловая система. Типы файлов.
- •18. Структура каталогов ос Linux. Файловая система ос Linux ext2fs, ext3fs.
- •Система адресации данных ext2 — это одна из самых важных составляющих фс. Она позволяет находить нужный файл среди множества как пустых, так и занятых блоков на диске.
- •19 Базовая файловая система s5fs.
- •Управление процессами в ос Unix. Типы процессов.
- •21Алгоритмы управления памятью в ос unix, Linux. Замещение страниц.
- •22. Загрузка ос Windows nt. Особенности Windows nt
- •23. Файловая система ntfs. Структура, особенности, преимущества ntfs
- •24. Управление памятью в Windows nt. Стратегии выборки, размещения и замещения страниц.
- •25. Язык Java. Особенности языка. Средства для разработки приложений. (jdk). Пакеты. Простейшая программа, компиляция и запуск.
- •26. Комментарии и встроенная документация. Спецификаторы доступа к классам и полям класса в Java. Public, protected и private
- •27. Интерфейсы Реализация интерфейсов. Ключевое слово static, ключевое слово this.
- •28. Апплеты. Структура и методы апплета. Вызов апплета.
- •29. Исключительные ситуации. Обработка исключительных ситуаций
- •30. Программирование отношений типа «Является», «Имеет», «Использует», «Создает».
- •31. Потоки Создание и запуск потока.
- •32. Синхронизация потоков.
- •33. Система ввода-вывода в Java. Работа с файлами.
- •34. Библиотека Swing. Основные компоненты Реализация пользовательского интерфейса.
- •35. Библиотеки jdbc, подключение к базе данных. (Объект Connection)
- •36. Реализация запроса sql и обработка результатов. (Объекты .Statement и Resultset)
- •37. Сервлеты, структура и организация. Методы жизненного цикла.
- •38. Jsp, структура и организация. Класс Session.
- •39. Основы технологии ejb. Основные цели. Ejb-компонента, ejb-объект, ejb- контейнер.
- •Цели, лежащие в основе технологии ejb
- •40 Entity Bean. Жизненный цикл.
- •41 Модели жизненного цикла
- •43 Диаграммы потоков данных
- •44 Функциональное тестирование
- •Функциональное тестирование включает:
- •45 Методы разработки программ (Метод джексона и метод Вареье орра)
- •46 Модели качества процессов конструирования.
- •47 Структурное программирование
- •48. Модульное программирование
- •49 Способы реализации алгоритмов
- •50 Методы доказательства правильности программ и алгоритмом
- •51 Центральные проекции
- •52 Параллельные проекции
- •53. Двумерные аффинные преобразования.
- •54. Трехмерные аффинные преобразования
- •55 Описание и построение составных поверхностей
- •56 Построение составных поверхностей Эрмита
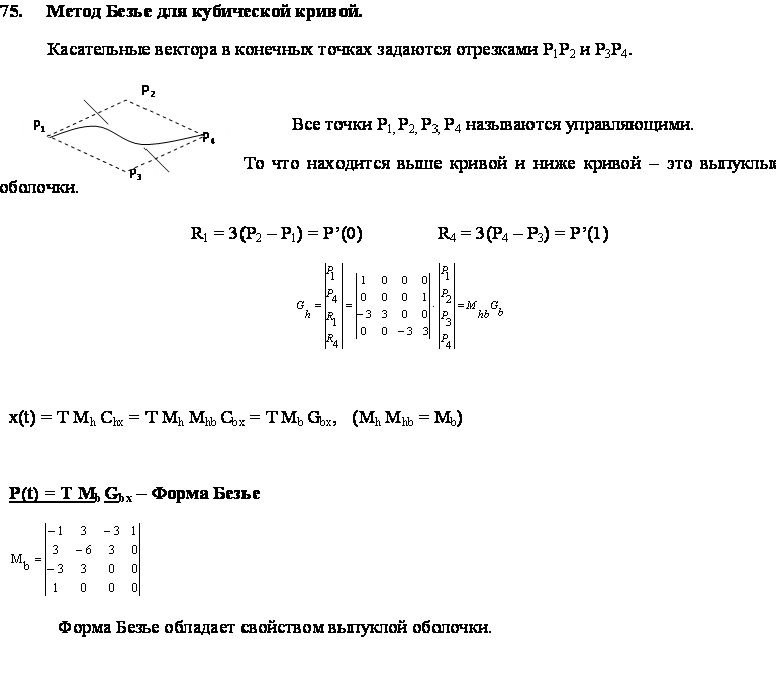
- •57 Построение составных поверхностей Безье
- •58 Построение составных поверхностей методом в-сплайнов
- •59. Классификация методов моделирования. Методы моделирования твердого тела.
- •60. Модели объемных тел . Алгебрологическая граничная модель.
- •61 Модели объемных тел. Модель конструктивной геометрии трехмерного объекта.
- •62. Модели объемных тел. Кусочно-аналитические граничные модели.
- •63 Классификация интеллектуальных ис
- •Структура экспертных систем (эс).
- •Этапы разработки эс.
- •Классификация эс.
- •Инструментальные средства разработки эс.
- •68 Системы, основанные на продукционных моделях представления знаний.
- •69 Семантические сети
- •70 Логический вывод на основе субъективных вероятностей
- •5.2. Распространение вероятностей в эс
- •72 Метод экспертного оценивания.
- •73. Классификация методов моделирования. Моделирование скульптурных поверхностей.
- •77. Основные классы задач, решаемые искусственными нейронными сетями (инс).
- •78. Математическая модель искусственного нейрона.
- •79 Основные этапы нейросетевого анализа.
- •80. Топологии искусственных нейронных сетей (инс). Многослойные сети. Классификация многослойных инс.
- •81 Обучение инс, парадигмы обучения. Правила Обучения.
- •83 Обучение инс. Обучение с учителем. Алгоритм обратного распространения ошибки
- •84 Обучение инс. Обучение без учителя. Алгоритм обучения Кохонена.
- •85 Обучение инс. Смешанное обучения. Сети встречного распространения
- •87 Каскадная схема проектирования ис
- •88 Бизнес-реинжиниринг в проектировании ис
- •89 Системное проектирование ис
- •90 Основные этапы проектирования ис
- •91 Построение диаграмм потоков данных (dfd) при проектировании ис
- •92 Модели субд при проектировании ис
- •93 Case- технологии в проектировании ис. Классификация case- средств.
- •94. Проектирование структуры бд, нормализация отношений.
- •96. Описание интегрированной модели сложной системы средствами языка uml. Концептуальные модели. Диаграмма вариантов использования.
- •101.Архитектура экономических информационных систем.
- •102.Жизненный цикл экономических информационных систем.
- •103.Этапы реинжиниринга бизнес-процессов в экономических системах.
- •104.Основные классы автоматизированных систем управления бизнес-процессами (mrPl, mrpii, erp).
- •105.Реинжиниринг бизнес-процессов на основе корпоративной ис.
- •106.Этапы проектирования кис.
- •107. Информационная поддержка этапов жизненного цикла кис (cals-технологии).
- •108. Средства концептуального проектирования кис (case-средства).
- •109.Технологии построения кис (клиент-серверные технологии).
- •110.Практическое использование интегрированных кис.
- •111 Приближенные числа и действия над ними. Классификация погрешностей.
- •121. Множества и способы их задания. Операции над множествами. Основные тождества алгебры множеств.
- •122. Бинарные отношения и их свойства. Специальные бинарные отношения.
- •123. Нечеткие множества и операции над ними.
- •125. Понятие графа. Способы задания графа. Основные операции над графами. Основные типы графов.
- •125 Достижимость и связность в графе. Определение компонент связности в неорграфах и сильных компонент в орграфах.
- •128 Эйлеровы и гамильтоновы циклы в графе. Алгоритм Флери построения эйлеровых циклов в графе. .Алгоритм Робертеса и Флореса по строения гамильтоновых циклов в графе.
- •129 Определение кратчайших путей и маршрутов в графе с использованием алгоритма Дейкстры.
- •133 Постановка задач линейной оптимизации. Прикладные линейные модели.
- •2 Задачи транспортного типа.
- •134 Методы решения задач линейной оптимизации.
- •135 Постановка задач дискретной оптимизации. Прикладные дискретные модели.
- •136. Методы решения задач дискретной оптимизации.
- •137. Постановка задач нелинейного программирования. Задачи выпуклого программирования. Функция Лагранжа, принципы ее построения. Метод множителей Лагранжа для решения задач на условный экстремум.
- •139. Постановка задач безусловной оптимизации. Классификация задач безусловной оптимизации и методов их решения. Методы нулевого порядка.
- •140. Постановка задач безусловной оптимизации. Классификация задач безусловной оптимизации и методов их решения. Градиентные методы оптимизации.
- •141. Постановка задачи безусловной оптимизации. Классификация задач безусловной оптимизации и методов их решения. Методы безусловной оптимизации Ньютоновского типа.
- •142. Методы решения задач условной оптимизации. Метод штрафных функций. Внутренние и внешние штрафные функции.
- •2) Учет функциональных ограничений. Для учета функциональных ограничений обычно используется метод штрафных функций.
- •145.Принципы построения программных комплексов принятия оптимальных решений. Основные требования к системам оптимизации. Классификация систем.
- •146.0Бъекты защиты информации. Классификация угроз безопасности; каналы утечки, воздействия. Цели и задачи защиты данных и ивс
- •148 Принципы организации систем обеспечения безопасности данных. Основные подсистемы, входящие в состав системы обеспечения безопасности данных.
- •147 Модель потенциального нарушителя. Классификация компьютерных преступлений. Способы мошенничества в информационных системах.
- •149.Стандарты информационной безопасности. «Критерии оценки безопасности компьютерных систем». Руководящие документы Гостехкомиссии России. «Единые критерии безопасности информационных технологий».
- •Основные элементы политики безопасности:
- •150 Классификация средств защиты данных. Физические средства защиты информации.
- •151 Криптографические методы и средства защиты данных, основные понятия, классификация
- •152 Классификация методов шифрования. Методы замены, перестановки, аналитических преобразований, гаммирования.
- •155. Защита компьютерных систем от вредоносных программ. Классификация вредоносных программ. Методы защиты.
- •156.Защита программных средств от несанкционированного использования и копи-
- •157.Методы и средства защиты информации от несанкционированного доступа. Аутентификация пользователей на основе паролей и модели рукопожатия. Аутентификация пользователей при удаленном доступе.
- •158.Защита информации от несанкционированного доступа в компьютерных сетях.
- •159.Реализация дискреционной и мандатной политики безопасности в ос семейства Windows.
- •160.Основные компоненты банка данных, классификация банков данных и требования к ним.
- •161.Концепция централизованного управления данными, функция администратора данных.
- •162. Архитектура систем баз данных, технология «клиент сервер».
- •163 Классические модели данных: иерархические сетевые, реляционные.
- •164.Реляционные объекты данных, целостность реляционных данных.
- •165Реляционная алгебра и реляционное исчичление
- •166 Язык реляционных бд sql. Структура запросов на языке sql.
- •170 Классификация моделей и их типы.
- •171 Требования, предъявляемые к математическим моделям, уровни моделирования
- •177 Оценка свойств математической модели технической системы
- •178 Распределение вероятностей
- •185. Основные технико-эксплуатационные характеристики эвм.
- •186. Классификация эвм по поколениям и по назначению, по функциональным возможностям и размерам.
- •188. Процессоры. Структура центрального процессора. Характеристики процессора.
- •189. Иерархическая структура памяти. Методы управления памятью.
- •190 Общие принципы организации системы прерывания программ. Характеристики системы прерывания.
- •191 Архитектура эвм, Однопроцессорные эвм, многопроцессорные эвм.
- •Mimd компьютеры
- •Многопроцессорные вычислительные системы
- •Многопроцессорные вычислительные системы с общей шиной.
- •Многопроцессорные вычислительные системы с многовходовыми модулями оп.
- •192 Организация кэш-памяти
- •193 Принципы организации подсистем ввода/вывода. Каналы ввода/вывода.
- •Принципы организации устройств ввода-вывода
- •194 Структура и форматы команд эвм
73. Классификация методов моделирования. Моделирование скульптурных поверхностей.
Используются 3 метода представления геометрической модели:
Моделирование и представление геометрической модели.
Формирование и описание геометрической модели
Отображение геометрической модели на графических устройствах.
Методы геометрического моделирования делятся на:
Методы моделирования твердого тела – предназначены для моделирования простых и сложных объектов. Решаются задачи синтеза геометрической модели из модели простых трехмерных объектов, называемых объемными примитивами или базовыми элементами формы. (Выделяется некоторый набор геометрических фигур,сфера, куб и т.д.). Этот набор должен быть достаточен для построения всего многообразия геометрических объектов в исследуемом классе задач. Такой набор непроизводных фигур составляет геометрическую базу. В качестве примитивов используют, , часто встречающиеся в технике тела и фигуры.)
Методы моделирования скульптурных поверхностей- используются в автомобильной и самолетной промышленности. Данный метод используется для проектирования динамических поверхностей. При проектировании данных поверхностей используется каркасно-кинематический метод, основанный на перемещении некоторых образующих по направляющим. Основным объектом моделирования является поверхность, которая устанавливается из некоторого дискретного набора точек или кривых.
Метод каркасной или проволочной модели- мало используется, Для описания модели используются объекты первого порядка – линии и ребра.
Методы моделирования скульптурных поверхностей. При моделировании скульптурных поверхностей решается:
задача аппроксимации (приближенное представление)- возникает при замене кривой или поверхности, описанных сложными функциями другими объектами, описанными более простыми уравнениями, без потери необходимой точности.
Задача интерполяции (приближенного восстановления)- связана с поиском гладких кривых или поверхностей , проходящих через множество заданных точек.
Задача сглаживания. Используется если необходимо, чтобы искомая кривая или поверхность описывалась функцией, обеспечивающей необходимую степень дифференцирования.
Существуют 2 способа представления кривых:
- с помощью функции переменных x,y,z, когда x=x, y=f(x);z=g(x)
- параметрическое представление кривой: AxT^3+BxT^2+CxT+dx


77. Основные классы задач, решаемые искусственными нейронными сетями (инс).
Под ИНС понимается вычислительные структуры. которые моделируют простые биологические процессы, ассоциируемые с процессами человеческого мозга. Элементарным преобразователем в ИНС является искусственный нейрон, аналог биологического нейрона.
Классы задач, решаемых ИНС:
1 .Классификация образов. Задача состоит в указании принадлежности входного образа (например, речевого сигнала или рукописного символа), представленного вектором признаков, одному или нескольким предварительно определенным классам. К известным Приложениям относятся распознавание букв и речи, классификация сигнала электрокардиограммы и клеток крови.
2. Кластеризация/категоризация. При решение задачи кластеризации , которая известна также как классификация «без учителя» т.е. отсутствует обучающая выборка с метками класса. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кластер. Известны случаи применения кластеризации для извлечения Знаний , сжатия данных и исследования свойств данных.
3. Аппроксимация функций. Предположим что имеется обучающая выборка (х1 у1)(х2 у2)…(xnyn) (пары данных вход/ выход), которая генерируется неизвестной функцией f(х) искаженной шумом Задача аппроксимации состоит в нахождение неизвестной функции F(х) и ее оценки.
Аппроксимация функций необходима при решении многочисленных Инженерных и научных задач моделирования.
4. Предсказание/прогноз. Пусть заданы n дискретных отсчетов{ y(tl),y(t2)...y(tn)} в последовательные моменты времени tl,t2...,tn. Задача состоит в предсказание значения у(tn+1) Некоторый будущий момент времени tm+i .Предсказание/прогноз имеет значительное влияние на Принятие решений в бизнесе, науки и технике. Предсказание цен на фондовой бирже и прогноз Погоды являются типичными приложениями технике предсказание/прогноз.
5. Оптимизация. Задачей алгоритма оптимизации является нахождение такого решения , которое удовлетворяет системе ограничений и максимизирует или минимизирует целевую функцию . Задача коммивояжера, является классическим примером задачи оптимизации .
6. Память, адресуемая по содержанию. В модели вычисления фон Неймона обращения к Памяти доступно только по средствам адреса, который не зависит от содержания памяти. Более Того , если допущена ошибка в вычисление адреса, то может быть найдена совершенно иная информация. Ассоциативная память или память, адресуемая по содержанию , доступна по указанию заданного содержания. Содержимое памяти может быть вызвано даже по частичному Входу или искаженному содержанию.
7. Управление. Рассмотрим динамическую систему, заданную совокупностью {u(t),y(t)}, Где u(t) является входным управляющим воздействием, a y(t) выходом системы в момент времени t . В системе управления с эталонной моделью целью управления является расчет Такого входного воздействия u(t), при котором система следует по желаемой траектории, диктуемой Эталонной моделью. Пример ом является оптимальное управления двигателем.
