§ 9.4. Закон инерции.

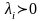Квадратичная форма может быть приведена к различным каноническим видам. Однако имеются такие характеристики коэффициентов канонических видов, которые остаются неизменными. Например, если квадратичная форма преобразуется к виду , где , , то соответствующая этой квадратичной форме функция в линейном пространстве неотрицательна, поэтому никакой другой канонический вид не может иметь отрицательных коэффициентов, т. е. существование отрицательных коэффициентов говорит о том, что функция может быть отрицательной. Другой важной характеристикой является ранг матрицы квадратичной формы.

Теорема. Ранг квадратичной формы не меняется при невырожденных заменах переменных и равен:

1. Числу отличных от нуля коэффициентов в любом ее каноническом виде;

2. Количеству ненулевых собственных значений матрицы квадратичной формы (с учетом их кратности).

Доказательство. При изменении базиса линейного пространства матрица квадратичной формы преобразуется по формуле , где - матрица перехода от базиса к базису. Матрица перехода является невырожденной, поэтому 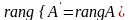, так как при умножении на невырожденную матрицу ранг не меняется.

Пусть квадратичная форма имеет два канонических вида:

и , причем , , , .

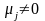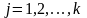Оба канонических вида – это квадратичные формы, представляющие одну и ту же функцию на линейном пространстве, но записанную в разных базисах. Поэтому одна каноническая форма из другой получается в результате замены базиса и ранги их матриц совпадают. Ранг квадратичной формы канонического вида равен числу ненулевых коэффициентов этой формы, т. е. 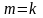. Доказано утверждение a) теоремы.

Квадратичную форму можно привести к каноническому виду ортогональным преобразованием. При этом коэффициенты квадратичной формы канонического вида (они же – диагональные элементы ее матрицы) будут собственными значениями матрицы исходной квадратичной формы. Доказано утверждение b) теоремы. Теорема доказана.

Теорема (закон инерции). Для любых двух канонических видов и , , , , одной и той же квадратичной формы:

1. и их общее значение равно рангу квадратичной формы;

2. количество положительных коэффициентов совпадает с количеством положительных коэффициентов ;

3. количество отрицательных коэффициентов совпадает с количеством отрицательных коэффициентов .

Доказательство. 1) Это утверждение доказано выше.

2) Пусть в этих двух канонических видах положительные коэффициенты предшествуют отрицательным, так что их можно переписать в виде:

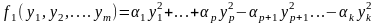, и ,

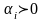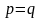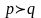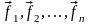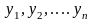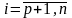
, , , . Этого можно добиться изменением порядка переменных. Надо доказать, что . Доказывать будем методом «от противного». Предположим, что . Обозначим и - базисы, в которых записаны канонические виды и квадратичной формы. Покажем, что существует ненулевой вектор с координатами в базисе и координатами в базисе , для которого одновременно выполняются условия , , . Координаты линейным образом выражаются через координаты : 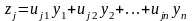, , где - матрица перехода от базиса к базису . Тогда условия для координат вектора представляют собой однородную систему линейных алгебраических уравнений:

Число уравнений 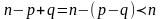, так как (по предположению), поэтому эта система имеет ненулевое решение, т. е. существует ненулевой вектор , для которого 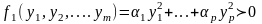, (хотя бы одно из ненулевое) и 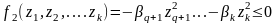. Таким образом, получили противоречие, что . Поэтому , т. е. количество положительных коэффициентов в двух различных канонических видах одной и той же квадратичной формы совпадает. 3) Так как совпадает в этих формах количество ненулевых коэффициентов, то из 2) следует и равенство количества отрицательных коэффициентов. Теорема доказана.