9. Квадратичные формы

§ 9.1. Определение и преобразование квадратичной формы.

Определение. Однородный многочлен второй степени от п переменных с действительными коэффициентами

, R, (9.1)

называется квадратичной формой.

Если в линейном п-мерном пространстве выбрать некоторый базис, то квадратичную форму можно рассматривать как числовую функцию, значение которой определено через вещественные координаты 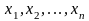вектора 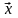: 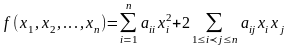, R

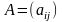
Покажем, что квадратичную форму можно записать в матричном виде , где  столбец, составленный из переменных,  симметрическая матрица п-го порядка, называемая матрицей квадратичной формы. Запишем квадратичную форму в виде 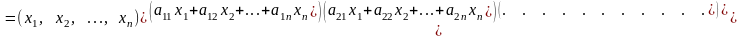= , т. е. . Верно и обратное, т. е. любая действительная симметрическая матрица является матрицей некоторой квадратичной формы.

Определение. Рангом и детерминантом квадратичной формы называются соответственно ранг матрицы квадратичной формы и ее определитель.

Определение. Если матрица имеет максимальный ранг, равный числу переменных п, то квадратичная форма называется невырожденной. Если ранг матрицы меньше числа переменных, то квадратичная форма называется вырожденной.

П р и м е р. Рассмотрим квадратичную форму от трех переменных . Эта квадратичная форма имеет матрицу . Определитель этой матрицы равен нулю, поэтому квадратичная форма вырожденная. В матричной записи квадратичная форма имеет вид:

.

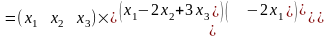
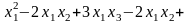
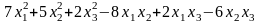
Квадратичная форма  невырожденная, так как ранг ее матрицы равен 3.

Пусть дана квадратичная форма , где 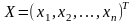. В n-мерном линейном пространстве L с фиксированным базисом она определяет функцию , заданную через координаты вектора в базисе . Найдем представление этой же функции в некотором другом базисе .

Пусть 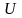- матрица перехода от базиса к базису . Тогда координаты вектора в старом базисе и координаты этого же вектора в новом базисе связаны соотношением:

.

Поэтому 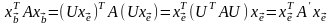, т. е. функция в новом базисе записывается при помощи квадратичной формы, причем матрица 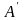этой квадратичной формы связана с матрицей исходной квадратичной формы соотношением .

Преобразование матрицы квадратичной формы называется заменой переменных в соответствии с формулой .

Замена переменных вида с произвольной матрицей называется линейной. Изменение базиса в линейном пространстве приводит к линейной замене переменных с невырожденной матрицей .

П р и м е р. Квадратичную форму преобразовать к новым переменным 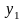, , ,если

Решение. Данная замена переменных в матричной записи имеет вид , где .

Тогда 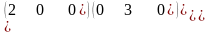. Таким образом, в новых переменных квадратичная форма принимает вид: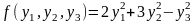 . Все коэффициенты при попарных произведениях обнуляются и остаются слагаемые с квадратами переменных.

§ 9.2. Квадратичные формы канонического вида.

Определение. Квадратичная форма , R, , не имеющая попарных произведений переменных, называется квадратичной формой канонического вида. Переменные , в которых квадратичная форма имеет канонический вид, называются каноническими переменными.

Один из методов преобразования квадратичной формы к каноническому виду путем замены переменных состоит в последовательном выделении полных квадратов. Такой метод называется методом Лагранжа. Рассмотрим его применение на примере.

П р и м е р. Квадратичные формы и привести к каноническому виду.

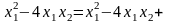
Решение. Рассмотрим . Для приведения ее к каноническому виду выделим полный квадрат по переменной : . Введем новые переменные 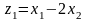, . Тогда - канонический вид.

Для второй квадратичной формы имеем:

,

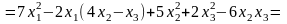
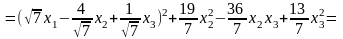
где , , .

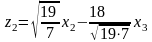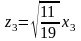В общем случае метод Лагранжа применяется следующим образом. Рассмотрим квадратичную форму общего вида , R от 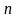переменных. Если , соберем все слагаемые формы, содержащие , и дополним их слагаемыми так, чтобы получился полный квадрат:

,

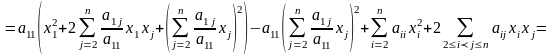
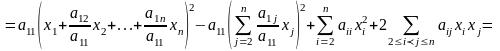
где , , , - квадратичная форма, не содержащая переменную .

С квадратичной формой можно поступить аналогично, выделяя полный квадрат по переменной . Продолжая процесс, квадратичную форму 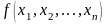преобразуем к виду:

,

где коэффициенты , , .

Выполним линейную замену переменных:

,

,

……………….,

,

,

……………,

.

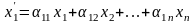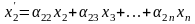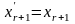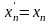Эта замена переменных определяется верхней треугольной матрицей , диагональные элементы которой равны 1, поэтому матрица - невырожденная. В результате замены переменных приходим к квадратичной форме 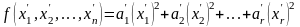, имеющей канонический вид.

Эта схема неприменима, если на каком-либо ее этапе в квадратичной форме нет соответствующей переменной во второй степени, например, . Тогда вместо можно остановить свой выбор на другой, квадрат которой существует в квадратичной форме.

Если в квадратичной форме нет ни одного квадрата, то перед выделением квадрата следует выполнить промежуточную замену переменных. Для этого выбираем произвольное слагаемое квадратичной формы. Пусть для определенности 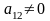, т. е. существует слагаемое . После замены переменных , , , …, 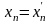получим квадратичную форму, у которой существует квадрат переменной 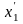, так как .

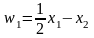Канонический вид, к которому приводится квадратичная форма, определяется неоднозначно. Например, квадратичная форма может быть приведена к каноническому виду , где , , но при замене переменных , канонический вид этой же квадратичной формы будет .
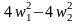