Постоянный ток

Сила тока: i =

где q - количество электричества, прошедшее чере^ поперечное сечение проводника за время t.

Плотность тока

где S - площадь поперечного сечения.

Закон Ома: 1) для однородного участка цепи

где R - сопротивление;

2) для неоднородного участка цепи

3) для замкнутой цепи

где R - сопротивление цепи; - ЭДС источников тока. Законы Кирхгофа:

1. для токов, сходящихся в узле =0

2. для замкнутого контура .

Работа и мощность тока на участке цепи

А= P=IU

полной цепи А=

Раздел IV. Магнитное поле в вакууме

Сила взаимодействия прямых параллельных токов I₁ и I₂:

где - магнитная постоянная; l- длина участка проводника, на который действует сила; r - расстояние между проводниками. Сила Ампера, действующая на проводник с током в магнитном поле,

F=I*l*B*sin

1 - длина проводника; В - магнитная индукция поля; - угол между векторами

l и В.

Сила Лоренца, действующая на заряженную частицу q, движущуюся со скоростью v в магнитном поле с индукцией В:

F=q*v*B*sin

где угол между векторами и

Закон Био-Савара-Лапласа dB = sin ,

где dl- длина проводника, г-расстояние от середины элемента проводника до точки, магнитная индукция в которой определяется, -угол между dl и г.

Магнитная индукция, созданная

1. прямолинейным проводником на расстоянии г

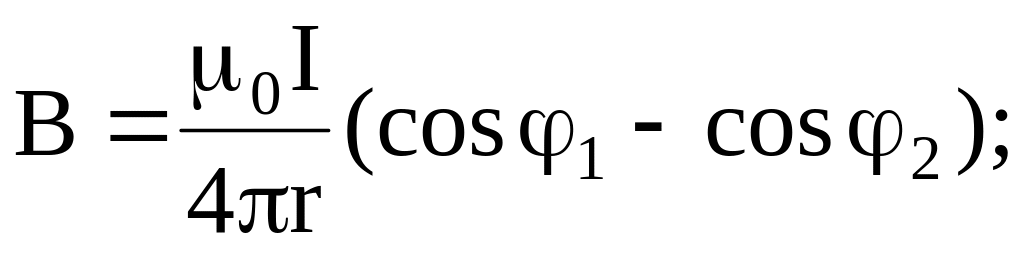
2. круговым током в центре В =

где r- радиус кривизны проводника;

3. бесконечно длинным проводником В = ,

где г-расстояние от оси проводника;

4. длинным соленоидом на оси где

где N-число витков; l-длина проводника; I-сила тока в одном витке. Поток вектора магнитной индукции через плоский контур площадью S

Ф=В_nS Ф=BScos

Работа сил магнитною поля А=I Ф

Закон Фарадея для электромагнитной индукции

для самоиндукции

где L- индуктивность контура.

Количество заряда, протекающего через сопротивление R при изменении магнитного потока q = Ф=LI

Индуктивность длинного соленоида L=

L = S L=

Экстраток замыкания и размыкания

при замыкании I₀=0, при размыкании =0.

Энергия магнитного поля W =

Объемная плотность энергии

где Н = напряженность магнитного поля.

Раздел V. Оптика

Закон преломления

где i - угол падения; r - угол преломления; n₁ и n₂ - абсолютные показатели преломления соответственно первой и второй сред; с - скорость света в вакууме; и - скорость света в среде.

Формула тонкой линзы

где F - фокусное расстояние линзы; d- расстояние от оптического центра линзы до предмета; f- расстояние от оптического центра линзы до изображения.

Оптическая сила: 1) линзы D =

2) системы линз D=D₁+D₂+...D_n.

Интерференционный mах: ;

min =(2k+1) ,

где - оптическая разность хода, - длина волны. Расстояние между интерференционными полосами полученными от 2-х когерентных источников х =

L - оптическая длина пути световой волны. Оптическая разность хода для тонкой пластинки при отражении

=2dncosr±

В отраженном свете: радиус темных колец Ньютона r =

радиус светлых колец Ньютона k =

где R радиус кривизны поверхности линзы, соприкасающейся с плоскопараллельной стеклянной пластинкой.

Для одной щели условие дифракции (min) ,

где d - ширина щели, - угол дифракции.

Условие главного mах для дифракционной решетки .

Разрешающая способность спектрального прибора R = ,

где - наименьшая разность длин волн двух соседних спектральных линий ( и ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; R=kN,

где N - число штрихов решетки.

Степень поляризации

где I_max и I_min - максимальная н минимальная интенсивности частично поляризованного света, пропускаемого анализатором. Закон Брюстера при отражение: tg i_p=n,

где i_p- угол падения, при котором отраженная световая волна полностью поляризована, n - относительный показатель преломления.

Закон Малюса: a) I=I₀cos²p (без поглощения);

б)I=(l-k)I_ocos² (k - коэффициент поглощения),

где I - интенсивность плоскополяризованного света, прошедшего через анализатор; I_о - интенсивность плоскополяризованного света, падающего на анализатор: - угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора.

-16-