31. Сила давления, действующая на плоскую и цилиндрическую стенку. Закон Архимеда. Гидростатическая подъемная сила.

1. Если применять закон Паскаля к реальной жидкости, имеющей вес, то к внешнему давлению необходимо прибавлять гидростатическое давление.

Гидростатическим называется давление воды, обусловленное ее тяжестью. Это название часто распространяют на все жидкости.

Выделим мысленно в жидкости на глубине h горизонтальную площадку S. На эту площадку будет давить сверху вес P столбика жидкости высотой h, причем

,

где — удельный вес жидкости, а V — ее объем. Ни , ни V не зависят от давления, так как жидкость несжимаема. Согласно формуле , где —плотность жидкости, а g—ускорение силы тяжести. Объем V=Sh. Поэтому

.

Гидростатическое давление р, производимое силой Р на площадку S, равно P/S, или

,

т. е. гидростатическое давление в любой точке внутри жидкости зависит только от глубины этой точки под поверхностью жидкости и от удельного веса жидкости.

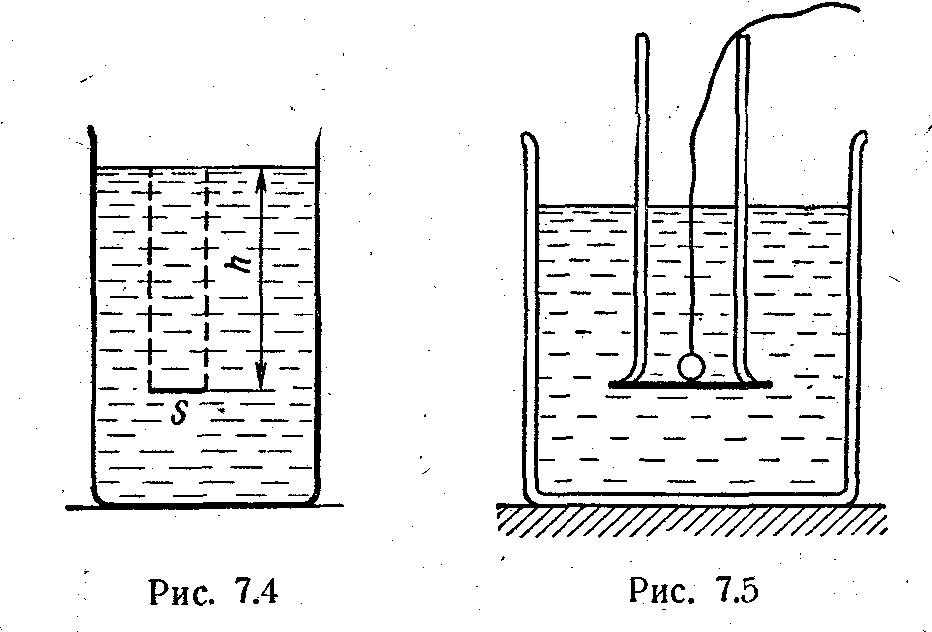
Г оризонтальная площадка S, выделенная в жидкости, находится в покое. Следовательно, она испытывает снизу такую же силу давления , как сверху. Это можно показать на следующем опыте. Опустим в сосуд с водой стеклянный цилиндр с очень легким приставным дном. Дно оказывается прижатым к цилиндру силой гидростатического давления, и цилиндр пуст. Наливая постепенно воду в цилиндр, можно убедиться, что дно оторвется от цилиндра, когда вода в нем достигнет того же уровня, что ив сосуде.

2. Гидростатическое давление на дно сосуда, в который налита жидкость с удельным весом до уровня Н, равно, согласно формуле,

Из этой формулы следует, что гидростатическое давление зависит от высоты столба жидкости, но не зависит ни от формы сосуда, ни от площади его дна. Следовательно, оно не зависит .и от веса жидкости, налитой в сосуд. Этим объясняется так называемый гидростатический парадокс: сила давления на дно может быть и больше веса жидкости в сосуде, и меньше его. Дело в том, что на жидкость действуют силы F со стороны стенок сосуда, перпендикулярные к стенкам и численно равные силам давления жидкости на стенки. В сосуде эти силы сжимают жидкость. В сосуде жидкость сжимается, горизонтальными составляющими сил F, а их вертикальные составляющие направлены вверх и уравновешивают часть веса жидкости. В сосуде вертикальные составляющие сил F направлены вниз и увеличивают силу, действующую на дно сосуда.

Интересный опыт был произведен Паскалем. Он вставил в верхнее дно бочки, наполненной водой, длинную тонкую трубку и стал наливать в трубку воду. Когда высота воды в трубке достигла нескольких метров, силы давления воды на стенки бочки разорвали ее.

Для этого понадобилась лишь пара литров воды в трубке.

4. Г идростатическое давление на стенки сосуда изменяется с глубиной, о чем можно судить по силе струи, вытекающей из боковых отверстий в сосуде с водой; Так как у самой поверхности жидкости (h==0) оно равно нулю, а у дна сосуда (h == Н) - , то силу давления на боковую стенку сосуда находят, как произведение среднего бокового давления рб.ср. яа площадь S стенки:

и

4. Если на жидкость действует внешнее давление , то полное давление р в жидкости равно сумме внешнего давления и гидростатического давления:

З акон Архимеда в применении к жидкостям. Рассмотрим силы гидростатического давления, действующие на твердое тело в виде прямоугольного параллелепипеда, опущенное в жидкость. Силы давления, действующие на боковые стенки тела, взаимно уравновешиваются. па верхнее основание действует сила гидростатического давления , направленная вниз и численно равная

,

где — глубина погружения верхнего основания площадью S.

На нижнее основание, находящееся на глубине под поверхностью жидкости, действует сила гидростатического давления направленная вверх.

Сила больше , поэтому тело -испытывает выталкивающую силу F, направленную вверх и численно равную

или -

где —объем жидкости, вытесненной телом, а — числовое значение веса жидкости, вытесненной телом. Поэтому можно считать, что сила F приложена в Центре тйжести тобъема V. Формула выражает

закон Архимеда:

любое тело, погруженное в жидкость, испытывает выталкивающую силу, которая численно равна весу жидкости, вытесненной телом, и приложена в центре тяжести вытесненного телом объема жидкости