Глава 3. Системы линейных уравнений.

Система линейных уравнений.

α₁₁x₁ + α₁₂x₂ + . . . + α_1nx_n = β1,

α₂₁x₁ + α₂₂x₂ + . . . + α_2nx_n = β2,

Матрица системы.

Это матрица составленная из коэфицентов при неизвестных элементов

Расширенная матрица.

Это матрица составленная из коэфицентов при неизвестных элементов и столбца свободных членов системы

Решения системы.

Мы находим все , ξ и они выполняют равентство ξ₁a₁ +. . . + ξ_na_n = b.

Совместные, несовместные, определенные и неопределенные системы. Критерии совместности и определенности.

Слн называется совместной если она имеет хотя бы 1 решение

Слн называется не совместной если она не имеет решений

Слн называется определенной если иммет 1 решение

Слн называется неопределенной имеет более одного решения

Теорема Крамера.

Если определитель системы n линейных урванений с n не известными не равен нулю, то эта система совместна и определена и ее единственное решение находится по формуле x_k= ||_k / ||

Решение систем в общем случае.

1. Выбрать базисный минор матрицы системы и выписать соответствующую ему базисную под систему

2. Обьявить свободными неизвестными те, коэф при которых не входят в базиснысный минор и перенести члены содержащие свободные неизвестные, направо

3. Обьявить свободные неизвестные параметрами и решить каким либо образом полученную систему r линейных уравнений с r несвободными неизвестными

Однородные системы линейных уравнений.

α₁₁x₁ + α₁₂x₂ + . . . + α_1nx_n = 0,

α₂₁x₁ + α₂₂x₂ + . . . + α_2nx_n = 0,

Свойства решений однородной системы Фундаментальная система решений однородной системы.

Сумма двух любых решений однородной системы линейных уравнений снова является решением этой системы.

Произведение любого числа α ∈ k на любое решение однородной системы линейных уравнений снова является решением этой системы

Теорема о числе решений в фундаментальных системах решений. Следствие.

Глава 4. Алгебра матриц.

Операции сложения матриц и умножения матрицы на скаляр, их основные свойства.

1)Сложение матрицы со скаляром

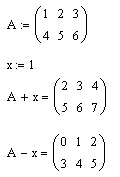
2)Умножение матрицы на скаляр

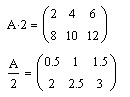
Умножение матриц.

Свойства умножения.

α (А + В) = αА + αВ

(α + β)А = αА + βА

(αβ)А = α(βА) = β(αА)

Транспонирование произведения матриц.

• 

Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.

Определитель произведения матриц.

ТЕОРЕМА 4.2.2 (о транспонировании произведения матриц). Если А и В таковы. что АВ существует, то (АВ)' = В'А'.

Доказательство. Так как АВ существует, то матрица А размерности m×n, В размерности n×p, тогда матрица АВ размерности m×p, а (АВ)' размерности p×m. Видно, что В' размерности p×n. А' размерности n×m. Ясно, что существует матрица В'А' и она имеет размерность p×m, то есть ту же что и матрица (АВ)'. Покажем равенство соответствующих элементов этих матриц. Обозначим (A)_ij, 1 ≤ i ≤ m, 1 ≤ j ≤ n элементы матрицы А, (B)_jk, 1≤ k ≤p — элементы матрицы В.

Получаем

(V 1 ≤ к ≤ р, 1 ≤ i ≤ m) ((АВ)')_ki = (В'А')_ki

Единичная матрица.

Определение 4.3.1. Единичной матрицей порядка n натыкается квад­ратная матрица n-порядка Е нида:

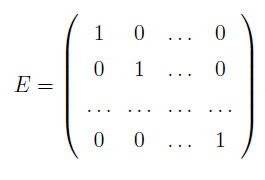
Обратная матрица.

Обратная матрица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E.

Единственность обратной матрицы.

Теорема об обратимости матриц. Следствие.

Матричные уравнения.

Матричная запись систем линейных уравнений и формул Крамера. Теорема о ранге произведения матриц и её следствие.