Программа
Глава 1. Определители.
Числовые кольца и поля.
Кольцо – числовое множество K, если оно содержит сумму,разность и
Полем Ненулевое числовое кольцо K, если оно содержит частное 2 любых своих чисел (знам отличен от 0)
Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов.
Число перестановок - число различных способов, которыми может быть упорядочено данное множество, состоящее из n элементов.
Инверсия- Взаимное расположение двух чисел в перестановке, когда большее стоит впереди меньшего
Перестановки четного типа - Перестановка с четным числом инверсий четного типа
Перестановки нечетного типа-перестановка с нечетным числом инверсий
Теорема о влиянии транспозиции на тип перестановки и её следствия.
Теорема: одна транспозиция меняет тип перестановки на противоположный
Следствие: Если n > 2, то количество четных перестановок из n символов равно количеству нечетных и равно n! / 2.
Определение определителя.
Квадратной
матрице 
-го
порядка ставиться в соответствие число
,
Свойства определителя:
При транспонировании квадратной матрицы её определитель не меняется:
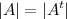
Общий множитель в строке можно выносить за знак определителя.
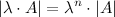
Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.
Если две строки определителя поменять местами, то определитель поменяет знак.
Определитель с двумя равными строками равен нулю.
Определитель с двумя пропорциональными строками равен нулю.
Определитель, содержащий нулевую строку, равен нулю.
Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
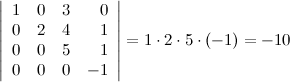
Определитель произведений матриц равен произведению определителей:
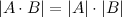
Минором для элемента аig называется определитель матрицы, полученный из исходной, вычеркиванием i-ой строки и g-ого столбца.
дополнительные миноры,
Алгебраические дополнения
Алгебраическое
дополнение элемента 
определителя 
-
определитель 
где 
-
минор элемента
.
Теорема Лапласа. Пусть D – определитель n-го порядка, в котором произвольно выбраны k строк (или столбцов), где 1 ≤k ≤ n – 1. Тогда определитель D равен сумме произведений всех миноров k-го порядка, расположенных в выбранных строках (или столбцах), на их алгебраические дополнения.
следствие: Сумма произведений всех элементов некоторой строки (столбца) матрицы А на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю