5. Ошибки измерений их классификация и свойства.

Ошибки измерений, их классификация и свойства.

Измерения сопровождаются ошибками. По источникам и характеру ошибки различны. Их можно разделить на грубые, систематические и случайные.

Грубые ошибки являются, как правило, следствием промахов,

просчетов в измерениях. Они обнаруживаются повторными измерениями. Поэтому контрольные измерения являются необходимыми для исключения грубых ошибок.

Систематические ошибки — такие, которые знаком и величиной однообразно повторяются в многократных измерениях. Источниками систематических ошибок являются неисправности в применяемых

инструментах, их неточная установка при измерениях, личные физиологические особенности наблюдателя, влияние внешних факторов.

Влияние систематических ошибок на результаты измерений сводят к допустимому минимуму путем тщательной поверки измерительных инструментов, применения соответствующей методики измерений, а также путем введения поправок в результаты измерений.

Случайные ошибки — такие, размер и характер влияния которых на каждый отдельный результат измерения остается неизвестным.

Величину и знак случайных ошибок заранее установить нельзя. Теоретические исследования и многолетний опыт измерений показывают, что случайные ошибки подчинены определенным закономерностям, и изучение их дает возможность получить наиболее надежный результат из совокупности измерений и оценить его точность.

Случайные ошибки характеризуются следующими свойствами:

1) при заданных условиях измерений случайные ошибки по своей абсолютной величине не могут превышать известного предела;

2) малые по абсолютной величине положительные и отрицательные ошибки равно возможны, причем малые ошибки появляются в измерениях чаще, чем большие;

3) среднее арифметическое из случайных ошибок измерений одной и той же величины стремится к нулю при неограниченном числе измерений.

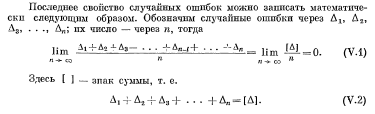
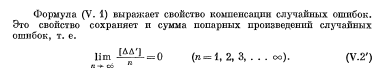
По источнику происхождения различают ошибки приборов, внешние и личные.

6. Законы распределения и основные характеристики точности. Доверительный интервал.

Законы распределения и основные характеристики точности. Доверительный интервал.

Все основные величины в качестве основной характеристики имеют закон распределения. Под законном распределения понимают вероятность того, что случайная величина меньше какого - то заданного числа А. Закон распределения может быть представлен в виде таблицы, аналитически (функция), графически (гистограмма).

Особую и исключительно важную роль в теории вероятностей играет нормальныйзакон распределения случайных величин. Это – наиболее часто встречающийся на практике закон распределения. Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности.Нормальный закон распределения также называется законом Гаусса.

Нормальный закон из следующих рассуждений.

Если необходимо определить вероятность того, что в независимых и равновероятных испытаниях нужное событие появится kраз из n, то используют известную формулу Бернулли

(1.2.6)

Здесь – число сочетаний из n по k, р – вероятность появления события в одном испытании (одинаковая для всех опытов), q= 1 –p. Использование этой формулы при достаточно больших значениях было очень трудоемко. Поэтому П. Лаплас предложил решение этой задачи, получившее название локальная теорема Лапласа: при постоянной и отличной от 0 и 1 вероятности появления события в каждом испытании, вероятностьP_n(k) того, что событие появится в n испытанияхkраз, приближенно равна (тем точнее, чем больше n) значению

(1.2.7)

где .

Для определения параметров в формуле (1.2.7) поступили следующим образом. Была рассмотрена случайная величина Х вида

хi	0	1
pi	q	p

где q= 1 – p. Её математическое ожидание есть

М_Х= 0 q+ 1 p = p,

а дисперсия

D_X= (0 – p)²q + (1 – p)²p= pq(p+ q) = pq.

Далее рассматривается составная случайная величина вида , когда x_j имеют определенное выше распределение и независимы. Тогда основные характеристики имеют вид

(1.2.8)

Такой результат следует из того, что (x_j)₁ = 0 cвероятностьюq если это событие не появляется в j– ом опыте а (x_j)₀ = 1 (j = 1n) если появляется с вероятностьюp. Тогда случайная величинаkтакже будет числом появлений события при nиспытаниях (сумма единиц).

Заменим в локальной теореме Лапласаk = Y,np = M_Y, и получим

. (1.2.9)

Полученная формула носит название формулы плотности распределения Гаусса (Муавра-Гаусса-Лапласа) и обозначается N(x; M_X, _X). К. Пирсонпредложил называть такой закон нормальным.

Закон χ2 Присона. Используется для статистической проверки гипотез и интервальной оценки исследуемых результатов.

Закон распределения Стьюдента. Используется для статистической проверки гипотез и интервальной оценки исследуемых результатов.

Закон распределения Фишера. Используется для статистической проверки гипотез.

Доверительный интервал – доверительным называется такой интервал, относительно которого с вероятностью β, сколь угодно близкой к 1 называемой доверительной, можно утверждать, что он содержит математическое ожидание параметра или его истинное значение при отсутствии систематических ошибок.