14. Виды проекций, их основные характеристики. Проекция Гаусса-Крюгера.

15. Редукции измерений на плоскость геодезической проекции.

Редукции измерений на плоскость геодезической проекции.

Редукция расстояний. Пусть S — длина стороны на поверхности

эллипсоида. Ее длина S на плоскости в проекции Гаусса — Крюгера при S≤30 км с достаточной точностью может быть вычислена по формуле

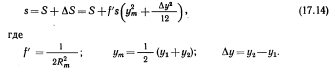
при S≤10 км второй член в скобках в формуле (17.14) можно не учитывать.

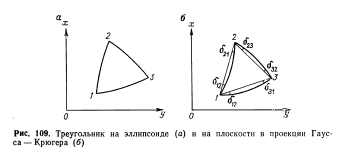
Поправки в направления за кривизну изображения геодезических линий на плоскости в проекции Гаусса — Крюгера. Стороны треугольников изображаются на плоскости в проекции Гаусса — Крюгера, как и на эллипсоиде, кривыми линиями (рис. 109). Решать на плоскости криволинейные треугольники нерационально. Вершины треугольников принято соединять прямыми линиями и затем решать такие треугольники, применяя простые формулы аналитической геометрии на плоскости. Поэтому необходимо перейти от углов между кривыми линиями к углам между хордами, соединяющими их концы.

Для этого в каждое измеренное направление Nik вводят

поправку δik за кривизну изображения геодезической линии на плоскости в проекции Гаусса — Крюгера. В триангуляции 2—4 классов поправки в прямое и обратное направления вычисляют по формулам

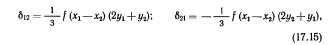
где f=p/2R²; х, у — приближенные координаты пунктов, км.

Ординаты y₁ и у₂отсчитывают от осевого меридиана зоны проекции, причем с положительным знаком к востоку от осевого меридиана, с отрицательным — к западу от него. В триангуляции 1 класса применяют более точные формулы.

В каждом треугольнике с вершинами 1, 2, 3 (рис. 109, б) найдем поправки δi в углы как разности

δ₁= δ₁₃-δ₁₂ δ₁= δ₂₃-δ₂₁δ₁= δ₃₂-δ₃₁

Контролем правильности вычисления поправок δ_ikв направления служит равенство: δ1+δ2+δ3=—Ɛ, где Ɛ— сферический избыток треугольника.

Переход от геодезических азимутов к дирекционным углам.

Дирекционный угол хорды S₁₂,соединяющей точки 1 и 2 на плоскости, при заданном азимуте А₁₂геодезической линии на поверхности эллипсоида между этими точками вычисляют по формуле

(17.17)

где — гауссово сближение меридианов на плоскости в точке 1; δ₁₂ — поправка (17.15) за кривизну изображения геодезической линии на плоскости.

16. Технические требования и способы высокоточных измерений горизонтальных углов.

Технические требования и способы высокоточных измерений горизонтальных углов

Классическими способами измерения горизонтальных направлений и углов являются:

Способ круговых приемов Струве:

Суть этого способа состоит в следующем. При неподвижном лимбе вращают алидаду теодолита по ходу часовой стрелки при КЛ и последовательно наводят зрительную трубу на направления О,А,В,С,N. и снова на начальное направление (т.е. замыкают горизонт)- это первый полуприем. Затем трубу переводят через зенит и, вращая алидаду против часовой стрелки при КП, наводят трубу на те же пункты, но в обратной последовательности: О,N,..С,В,А,О, т. е. выполняют второй полуприем. Два полуприема составляют один прием измерений. См стр. 58 шароглазова

Вес программы измерений вычисляется по формуле P=2*m , где m- число приемов. Число приемов рассчитывается в зависимости от класса по формуле P=2*m, вес задается инструкцией в зависимости от класса.

Между приемами всегда выполняется перестановка лимба на величину δ, рассчитываемую по формуле : δ = ( + ) , где i- цена деления лимба. Это компенсирует влияние систематических ошибок и случайных ошибок лимба.

Контроли между приемами: замыкание горизонта для 2 кл ≤5" , для 3 кл ≤6" , коллимационная ошибка ≤20’’, колебание коллимация в приеме 8’’ и 10’’ соответственно, расхождение направлений между приемами для 2 кл ≤5" , для 3 кл ≤6", чмсло повторных измерение≤30

Способ всевозможных комбинаций Гаусса – Шрейера- Суть этого способа состоит в измерении на пункте углов во всех комбинациях, образующихся при попарных сочетаниях всех направлений. Общее число углов r = , где n- число направлений.

Вес уравненных на станции направлений Р = n*m .

Основные требования :1) Р=const для всех пунктов сети одного класса , 2) каждое направление на пункте необходимо измерять при одном и том же положении лимба по возможности только 1 раз , достигается двойной перестановкой лимба :

- между приемами δ = +

- между углами σ = + - при n – нечетном , σ = + - при n – четном .Наблюдения выполняют по таблице рабочих установок.

Методика измерения отдельного угла в приеме

Пользуясь таблицей рабочих установок лимба, на горизонтальном круге устанавливают необходимый отсчет. Затем наводят трубу на левый предмет, т.е. А, и берут отсчет . Вращая по ходу часовой стрелки, на правое направление В и берут отсчет ( первый полуприем).

Рис. 8.2. Измерение угла в СВК

Далее приступают к выполнению второго полуприема. Для чего переводят трубу через зенит и, вращая алидаду по ходу часовой стрелки, вновь наводят на правый предмет, т.е. В, и берут отсчет Затем вращением алидады по ходу часовой стрелки наводят трубу на левый предмет и берут последний отсчет .

Таким образом, в первом полуприеме измеряют угол А.В, а во втором – его дополнение до 360^о, т.е. (360^о— А.В) (рис.8.2).

Данная программа наблюдений является оптимальной, т.к. она позволяет уменьшить влияния кручения знака и азимутального смещения лимба на результаты угловых измерений, что легко прослеживается из следующих рассуждений.

Контроль: значение углов в полуприемах КЛ и КП не должны расходится более 8" , колебание углов для 1 кл. между приемами 4-5" , различие между измеренными и вычисленными значениями углов 3-4" .

Способ неполных приемов Аладжалова Способ неполных приемов применяется при числе направлений n  7. Он сочетает в себе два классических способа измерения углов и создан с целью уменьшения недостатков этих способов, имеющих место при большом числе направлений (малое число приемов в СВК, необходимость видимости по всем направлениям в СКП, возрастание влияния кручения сигнала в СКП, значительная трудоемкость СВК и др.).

Программа наблюдений в способе Аладжалова строится следующим образом. Вначале выписываются все углы, которые необходимо измерить в СВК, а затем каждые 3 угла объединяются в группы из 3-ех направлений. Каждая группа измеряется способом круговых приемов без замыкания. Сложно составить программу наблюдений.

Способ Томилина или видоизмененный способ всевозможныхкомбинаций

В этом способе измеряются все углы, образующиеся каждой парой смежных направлений и покрывающие горизонт (рис. 9.2), т.е.

1.2 2.3 3.4 4.5 … (n – 1). nn.1,

Рис. 9.2. Иллюстрация к способу Томилина

а также углы являющиеся суммой двух смежных углов, т.е

1.3 2.4 3.5 … (n – 2). n(n-1).1 n.2

При n>5 в этом способе будет измеряться меньше углов, чем в способе всевозможных комбинаций.