6. Критерий Стьюдента

t-критерий Стьюдента применяется, когда необходимо сделать статистический вывод, равно ли математическое ожидание M{Х} генеральной совокупности некоторому предполагаемому значению С или ког­да требуется построить доверительный интервал для M{Х}. Обнаруже­но, что случайная величина t (при независимых наблюдениях) распреде­лена по закону Стьюдента, если Х распределена нормально: где N- общее число наблюдений (объем выборки), Х - среднее арифметическое случайной переменной Х; S{Х), S{X}- среднеквадратическое отклонение соответственно единичных значений Х и среднего арифметического Х.

7. Критерий Фишера

Критерий Фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей, распределенных по нормальному закону. F-критерий Фишера называют дисперсионным отношением, так как он формируется как отношение двух сравниваемых несмещенных оценок дисперсий:причем в числителе ставится большая из двух дисперсий.

13. Приведение измерений к центрам геодезических пунктов.70

Приведение измерений к центрам геодезических пунктов.

При угловых измерениях на каждом пункте необходимо, чтобы ось вращения теодолита J, установленного на столике сигнала, и ось симметрии визирного цилиндра V находились на одной отвесной линии, проходящей через центр пункта в точке O (рис. 1.) Однако в действительности такого совпадения нет. Поэтому перед началом наблюдений на пункте и после их окончания определяют элементы центрировки теодолита (е, Ө) и элементы редукции визирной цели (е₁, Ө₁), называемые элементами приведения, а затем вычисляют поправки в измеренные направления за центрировку и редукцию.

Рис. 1. Элементы приведения на пункте триангуляции

ОJ = e — линейный элемент центрировки; — угловой элемент центрировки;OV =e₁ — линейный элемент редукции; ₁— угловой элемент редукции;

(Для определения элементов приведения над центром пункта устанавливают облегчённую мензулу или столик, на горизонтальную поверхность которого прикрепляют центрировочный лист и стрелкой показывают направление на север. Затем с помощью вспомогательного теодолита, установленного на расстоянии примерно в полтора раза больше, чем высота геодезического сигнала, проектируют на этот лист ось вращения теодолита и ось визирного цилиндра. Проектирование выполняют с трёх установок теодолита. Аналогичным образом при трёх установках теодолита проектируют центр пункта на этот лист. При этом образуется треугольник погрешностей. Точки J и V соединяют с точкой О и линейкой измеряют с точностью до 0,001 м линейный элемент центрировки e = OJ и линейный элемент редукции e’ = OV. В точках J и V большим транспортиром с точностью до 15' измеряют углы Ө, Ө1.)

Возникает задача согласования результатов угловых наблюдений, т.е. приведения их к центрам знаков. Для чего в каждое наблюдаемое на знаке направление должны быть введены две поправки:

а) поправка за несовпадение центра вращения теодолита с центром знака или поправка за центрировку (с);

б) поправка за несовпадение наблюдаемого визирного цилиндра с центром знака ( ).

П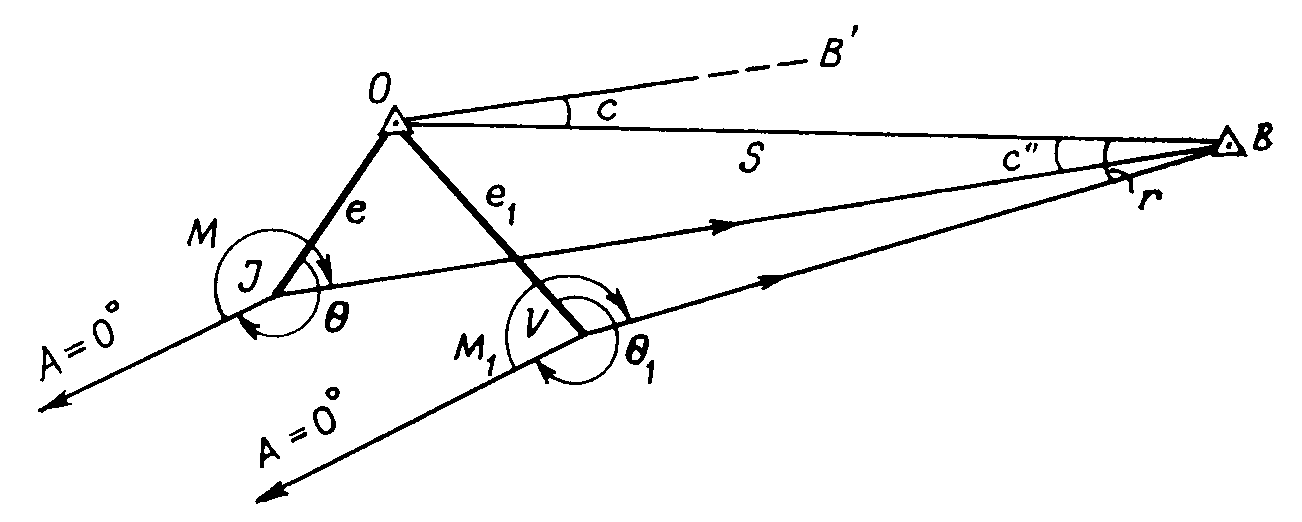 оясним эти поправки. Пусть на пункте с центром в точке 0 выполняются угловые измерения. Теодолит находится в точке J , визирный цилиндр в точке V (рис. 2). Из точки J проведем направление JА = 0˚ на начальный пункт А и направление JВ на какой- либо другой пункт В ; из точки V — направления VА и VВ на те же пункты. Обозначим через М — измеренные направления на пункте, отсчитываемые от начального. Проведем из точки 0 направление 0В' параллельно направлению JВ. Угол с" = В' 0В равен поправке за центрировку теодолита в измеренное направление JВ, введя которую получаем искомое направление 0В между центрами пунктов 0 и В. Решив треугольник J0В , в котором S = длина стороны между пунктами 0 и В, а 0JВ= (М+ — 360˚), запишем теорема sin

Рис. 2. Поправка в направление за центрировку теодолита и редукцию визирной цели

Ввиду малости с формулу (10.1) можно записать в виде:

(10.2)

Поскольку визирная цель V находится не над центром пункта 0, измеренное на пункте В направление ВV следует исправить поправкой r = 0ВV за редукцию визирной цели, чтобы получить направление ВО. Решив треугольник 0ВV, , 0VВ= (М₁+ ₁— 360˚), найдем малый угол r- поправка за редукцию:

(10.3)

В (10.2) и (10.3) e и – соответственно, линейный и угловой элементы центрировки на пункте 0; e₁ и ₁ – линейный и угловой элементы редукции на пункте 0; S – расстояние от пункта наблюдения до наблюдаемого пункта; M- значение измеренного направления на пункт, для которого вычисляются поправки.

Следует отметить, что поправки за центрировку теодолита вводят в направления, измеренные на пункте 0, а поправки за редукцию визирной цели со своим знаком — в обратные направления АV, ВV, поскольку визирование с пунктов А, В производится не на центр пункта 0, а на визирную цель V, не совпадающую с ним.

Итог:

Поправки за центрировку и редукцию угловых измерений вычисляют по формулам

Обозначения см. в (10.2) и (10.3).

А для линейных измерений — по формулам 10.7

(10.7)

В 10.7с и r — поправки за центрировку и редукцию измеренной линии.