Общие сведения

Главные характеристики случайной величины

Для численной характеристики СВ используют моменты k-порядка

1)Характеристикой центра распределения является так называемое математическое ожидание случайной величины, определяемое в виде

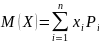
2)Характеристикой рассеяния случайной величины относительно

центра распределения является так называемая дисперсия, определяемая формулой

X – теоретическая случайная величина

X – практическая величина

3) стандарт

Дополнительные характеристики случайной величины

1. коэффициент вариации - относительная мера рассеивания

2. мода – величина, вероятность появления кот максимальна

3. асимметрия – мера скошенности

4. эксцесс – мера крутости

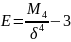
5)медиана – такое значение СВ, относительно которого вероятность появления значения больше или меньше равно 0,5.

Одним из наиболее часто встречающихся распределений является нормальное распределение. Оно играет большую роль в теории вероятностей и занимает среди других распределений особое положение. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях.

Если предоставляется возможность рассматривать некоторую случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения. Суммируемые случайные величины могут подчиняться каким угодно распределениям, но при этом должно выполняться условие их независимости (или слабой зависимости). При соблюдении некоторых не очень жестких условий указанная сумма случайных величин подчиняется приближенно нормальному закону распределения и тем точнее, чем большее количество величин суммируется.

Ни одна из суммируемых случайных величин не должна резко отличаться от других, т. е. каждая из них должна играть в общей сумме примерно одинаковую роль и не иметь исключительно большую по сравнению с другими величинами дисперсию.

Так как нормальному закону подчиняются только непрерывные случайные величины, то это распределение можно задать в виде плотности распределения вероятности.

Условием возникновения нормального распределения являются формирование признака как суммы большого числа взаимно независимых слагаемых, ни одно из которых не характеризуется исключительно большой по сравнению с другими дисперсиями.

Определение: Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

,

Параметр а- есть математическое ожидание НСВХ, имеющей нормальное распределение,σ² – дисперсия

Для проверки нулевой гипотеза используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Ее обозначают t если она распределена по закону Стюдента, X² - по закону "хи квадрат", F- по закону Фишера, G - по закону Кохрэна. Обозначим эту величину К