2) Количество информации – «I» – вероятностный (энтропийный) подход

Объемный подход - любое сообщение состоит из совокупности символов данного алфавита. Если принять сообщение из одного символа за единицу, то объём равен количеству символов в этом сообщении. Так как существуют разные алфавиты, то и различны единицы измерения. Двоичные системы: биты, десятичные: диты.

Энтропийный (вероятностный) подход – основан на том, что факт получения информации связан с уменьшением неопределённости (или энтропии) системы. То е количество информации в сообщении определяется как мера уменьшения неопределённости состояния данной системы после получения сообщения. Здесь под неопределенностью определяется, насколько мало известно наблюдателю о данной системе. Получаемая информация снижает энтропию системы. Таким образом, при энтропийном подходе под информацией понимается количественная величина исчезнувшей в ходе какого-либо опыта неопределённости. При этом в качестве меры неопределенности вводится энтропия – «H», кол-во информации:

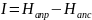
Н_апр – априорная энтропия о состоянии исследуемой системы.

Н_апс – апостериорная энтропия о состоянии исследуемой системы.

Априори – понятие, характеризующее значение до опыта или испытания и не зависимое от него.

Апостериори – происходящее из опыта или испытания.

В случае, когда в ходе испытания имевшееся неопределенность снята, то есть получен конкретный результат, Н_апс=0, то I=Н_апр.

Рассмотрим в качестве исследуемой системы дискретный источник информации, имеющий конечное множество состояний {a_i}.

В теории информации все множество состояний системы называют абстрактным алфавитом (или алфавитом источника сообщения). Отдельные состояния a_i называются буквами или символами алфавита. В каждый момент времени система может принять какое-то значение «a_i». Различные состояния реализуются вследствие выбора их источника и выбираются они хаотично. В общем случае источник характеризуется всей совокупностью состояний с вероятностью «p» их появлений, составляющими в сумме единицу.

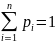
Меру неопределенности выбора состояния источника можно рассматривать и как меру количества информации, получаемой при полном устранении неопределенностей относительно состояния источника. Эта мера должна удовлетворять ряду естественных условий, одним из которых является необходимость монотонного возрастания количества получаемой информации с увеличением возможностей выбора, то есть числа N возможных состояний источника. При этом недопустимые состояния, вероятность которых p_i=0 не должны учитываться, так как они не меняют неопределенности.

Отсюда, казалось бы, что за меру неопределенности можно было бы взять число состояний N, предположив равновероятность состояний, но это не так.

При N=1 неопределенность отсутствует, и такая мера бы давала значение 1, а должен быть 0. Поэтому в качестве меры неопределенности источника с равновероятными состояниями приняли логарифм.

Эта мера была предложена американским учёным Рольфом Хартли в начале XX века. Основание логарифма здесь не имеет принципиального значения и определяет только масштаб или единицу измерения. Биты – основание два. Наты – основание e. Диты – основание десять. Так как в основном используется двоичная система, логарифм по основанию два.

Например, для снятия неопределенности в ситуации из двух равновероятных событий нужен один опыт и, следовательно, один бит информации. Четыре равновероятных – 2. Восемь – 3. То есть, количеств информации равно степени, в которую нужно возвести число 2, чтобы получить число равновероятных вариантов выбора.

Но равновероятных событий практически не бывает. Американский ученый Клод Шеннон обобщил понятие меры неопределенности H на случай, когда энтропия зависит не только от числа состояний, но и от вероятности их появления P_i.

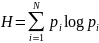
Это энтропия дискретного источника, которая представляет собой неопределенность, приходящуюся в среднем на одно состояние. В случае равновероятных состояний, когда , формула Шеннона преобразуется в формулу Хартли. Используя эти две формулы, можно определить избыточность D источника сообщений A, которая показывает, насколько рационально применяются символы данного алфавита:

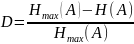
H_max – максимально возможная энтропия по формуле Хартли, Н(А) – по Шеннону. Суть данной меры заключается в том, что при равновероятном выборе ту же информационную нагрузку на знак можно обеспечить, используя алфавит меньшего объема, чем в случае с неравновероятным выбором. Пример: сравним русский и латинский алфавит. На основании эксперимента определены вероятности использования букв: H(рус)=4.35 бит на символ. H(лат)=4.03 бит на символ. Это по Шеннону.

По Хартли:

H_max(рус) = log₂ 33 = 5 бит на символ

Н_max(лат) = log₂27 = 4.75 бит на символ

Следовательно, D(рус)=0.13, D(лат)=0.15 неравномерность распределения букв латинского алфавита, чем у источника русского алфавита.