1. Метод Рунге-Кутта первого порядка точности ( )

Этот метод получается в том случаи, когда . Тогда мы имеем лишь один неизвестный численный параметр из группы параметров : .

Формула (5) методов Рунге-Кутта принимает следующий вид: (5`), где .

Локальная погрешность формулы (5`): , . Продифференцируем по : , ,…

Вычислим значение ; . Для того чтобы равенство выполнялось необходимо для любой непрерывной функции ; . Следовательно, порядок точности . Тогда формула (5`) перепишется в виде: (9).

Локальная погрешность формулы (9): (10).

Глобальная погрешность метода: .

Отбрасывая эту погрешность в формуле (9) и переходя к обозначению , получаем следующую расчётную формулу данного метода Рунге-Кутта первого порядка точности: (11). Данная формула (при ) совпадает с расчётной формулой метода Эйлера.

Метод Рунге-Кутта первого порядка точности (11) имеет квадратурный смысл формулы левых прямоугольников.

Определение. Метод имеет порядок точности, если его локальная погрешность на , а глобальная погрешность – на .

2. Методы Рунге-Кутта второго порядка точности ( )

Этот метод получается в том случаи, когда . Тогда мы имеем четыре неизвестных численных параметра из группы параметров , и : , , , , тогда формула (5) методов Рунге-Кутта принимает следующий вид: (5``), где , .

Для нахождения числовых параметров , , и поступают следующим образом:

1. Строятся разложения в ряд Тейлора в окрестности точки по степеням

левой и правой частей формулы (5``), то есть функций и ;

2. За счёт выбора параметров пытаются приравнять слагаемые в левой и правой частях формулы (5``) с одинаковыми степенями .

Если выполнить указанные действия, то в полученных разложениях удаётся приравнять слагаемые до второго порядка включительно.

Таким образом, локальная погрешность формулы (5``) является величина порядка , а для нахождения неизвестных параметров возникает следующая система равенств:

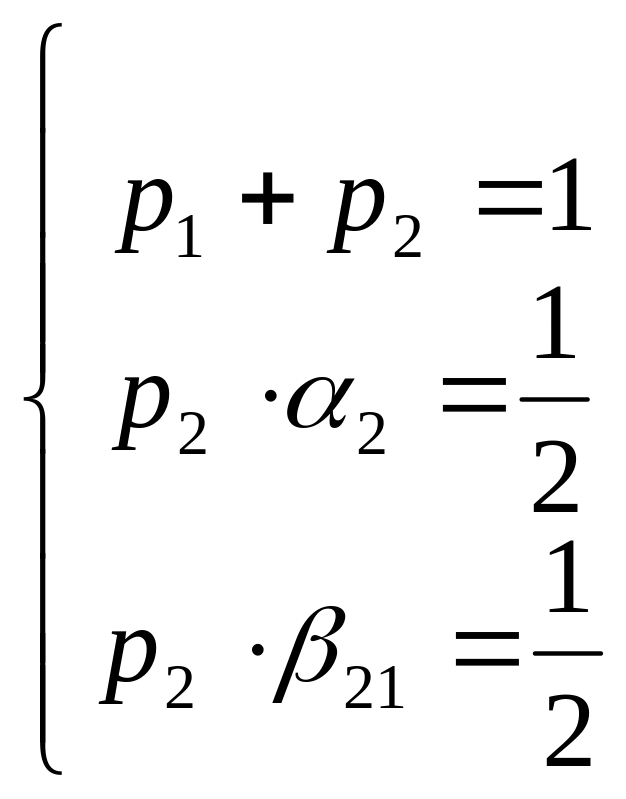
Это нелинейная система трёх уравнений относительно четырёх неизвестных. Она имеет бесконечное множество решений, то есть существует бесконечное множество методов Рунге-Кутта второго порядка точности.

Параметр объявляется свободным параметром (может принимать любые значения кроме ). Тогда можно выразить:

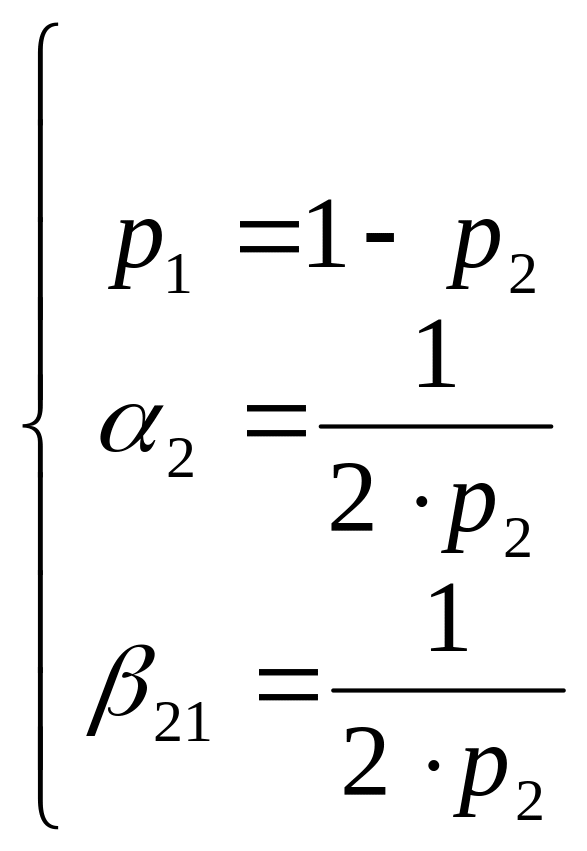
Значение параметра обычно выбирают так, чтоб формулы (5``) были удобны для вычислений.

Рассмотрим два наиболее употребляемых частных случая методов Рунге-Кутта второго порядка точности:

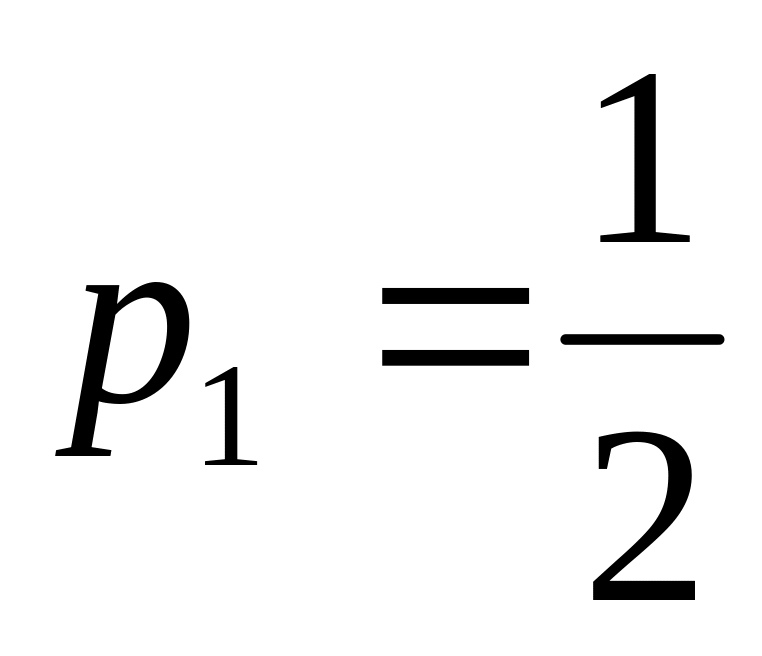1. , тогда , . Из формулы (5``) вытекает следующее: 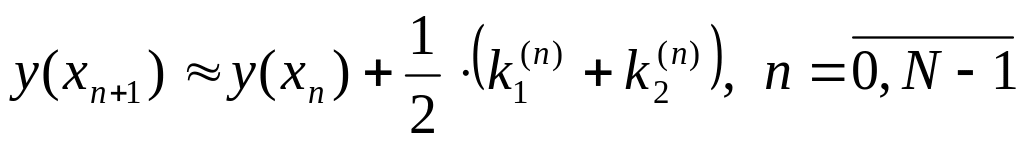(12), где

- аналог квадратурной суммы для вычисления определённого интеграла; ; .

Выясним квадратурный смысл формулы (12). Рассмотрим: , где – отрезок ряда Тейлора при разложении функции в окрестности точки . Отсюда следует, что линейная комбинация величин в формуле (12) является аналогом квадратурной формулы трапеций для приближённого вычисления интеграла в правой части формулы (3). Переходя в формуле (12) к обозначению , получаем следующую расчётную формулу методов Рунге-Кутта второго порядка точности: , где ; .

2. , тогда , . Из формулы (5``) вытекает следующее: 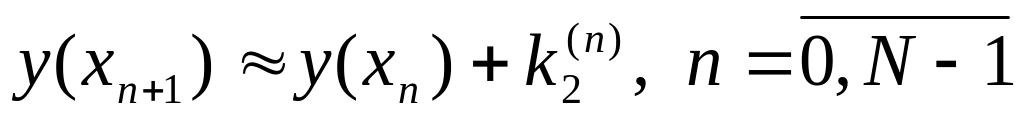(13), где

, , а – отрезок ряда Тейлора при разложении функции в окрестности точки .

Тогда – аналог квадратурной суммы формулы средних прямоугольников для приближённого вычисления интеграла в правой части формулы (3). Переходя к обозначению , можно на основе формулы (13) выписать расчетные формулы соответствующего метода типа Рунге-Кутта.