
- •6.040302 Інформатика
- •Квадратурные формулы Ньютона-Котеса
- •Частные случаи формул Ньютона-Котеса
- •Квадратурные формулы наивысшей алгебраической степени точности (н.А.С.Т.)
- •Квадратурная формула Гаусса (частный случай квадратурной формулы н.А.С.Т. При )
- •Смысл введения весовой функции
- •Методы решения задачи Коши для обыкновенных дифференциальных уравнений (оду)
- •Метод Рунге-Кутта первого порядка точности ( )
- •Методы Рунге-Кутта второго порядка точности ( )
- •Методы Рунге-Кутта третьего порядка точности ( )
- •Методы Рунге-Кутта четвёртого порядка точности ( )
- •Метод первого порядка точности
- •Метод второго порядка точности
- •Методы решения граничных (краевых) задач для обыкновенных дифференциальных уравнений (оду)
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
Дніпропетровський національний університет імені Олеся Гончара
Факультет прикладної математики
Кафедра обчислювальної математики та математичної кібернетики
Конспект лекцій
з дисципліни
“ЧИСЕЛЬНІ МЕТОДИ”
для студентів напряму
6.040302 Інформатика
Укладач: доцент кафедри ОМ та МК
канд. фіз.-мат. наук, доц.
Гарт Л.Л.
Дніпропетровськ
2012
Среди типичных классов математических задач можно выделить следующие наиболее важные:
задачи анализа (приближение функций, дифференцирование, интегрирование);
задачи алгебры (решение алгебраических и трансцендентных уравнений и их систем, решение проблемы собственных значений матрицы);
задачи решения дифференциальных и интегральных уравнений;
задачи оптимизации.
Вычислительная математика – это раздел математики, который разрабатывает методы решения практических задач и изучает вопросы применения этих методов с использованием вычислительной техники.
Приближение функций
Постановка задачи
Постановка задачи приближения функций
состоит в приближенной замене функции
![]() заданной в аналитическом виде или в
виде таблицы своих значений некоторой
функцией
заданной в аналитическом виде или в
виде таблицы своих значений некоторой
функцией
![]() более удобной для вычислений и такой,
что для всех интересующих нас значений
более удобной для вычислений и такой,
что для всех интересующих нас значений
![]() :
:
![]() .
.
Среди методов приближения функций можно отметить следующие:
интерполирование;
приближение функций при помощи сглаживающих или интерполяционных сплайнов;
с помощью равномерного приближения в нормированном пространстве;
среднеквадратическое приближение;
приближение с помощью генетических алгоритмов
приближение с помощью последовательных оптимальных алгоритмов.
Интерполирование
Постановка задачи интерполирования
Пусть на отрезке
![]() заданы
заданы
![]() попарно различных точек
попарно различных точек
![]() – узлы интерполяции (
– узлы интерполяции (![]() ).
Пусть известны значения функции
в этих точках:
).
Пусть известны значения функции
в этих точках:
![]() .
Надо построить такую приближающую
функцию
,
которая принадлежала бы известному
классу функций и принимала в узлах
интерполяции те же значения что и
:
.
Надо построить такую приближающую
функцию
,
которая принадлежала бы известному
классу функций и принимала в узлах
интерполяции те же значения что и
:
![]() (1)
(1)
Функция называется интерполирующей функцией для функции , а условие (1) – условием интерполирования.
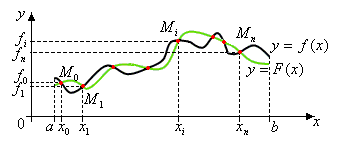
Геометрически задача интерполирования
состоит в том, чтоб построить кривую
![]() ,
проходящую через заданную систему точек
,
проходящую через заданную систему точек
![]() .
.
Интерполирующая функция
используется для приближённого вычисления
значений функции
в точках
![]() отличных от узлов интерполяции.
отличных от узлов интерполяции.
Различают интерполирование в узком
смысле, когда интересующая нас точка
попадает в промежуток
![]() и экстраполирование, когда
и экстраполирование, когда
![]() или
или
![]() .
При экстраполировании допускается
наибольшая погрешность приближения.
.
При экстраполировании допускается
наибольшая погрешность приближения.
Для получения наиболее точного приближения функции при помощи интерполирующей функции , свойства и необходимо согласовывать. Например, если достаточно гладкая функция, то в качестве надо использовать алгебраические многочлены. Если же периодическая функция, то в качестве надо брать тригонометрическую функцию с таким же периодом.
В такой общей постановке задача интерполирования может иметь бесконечное количество решений или не иметь их вообще. Нас интересуют задачи, которые обладают единственным решением.
Среди способов интерполирование важное место занимает линейное.
Линейное интерполирование
Пусть на отрезке заданы попарно различных и не обязательно равноудалённых точек и : . Интерполирующую функцию будем искать в следующем виде:
![]() ,
(2),
,
(2),
где
![]() - некоторые известные линейно независимые
функции на отрезке
;
- некоторые известные линейно независимые
функции на отрезке
;
![]() - числовые коэффициенты, подлежащие
определению.
- числовые коэффициенты, подлежащие
определению.
В качестве системы функций
![]() можно выбирать последовательность
следующих функций:
можно выбирать последовательность
следующих функций:
Неизвестные коэффициенты
![]() в формуле (2) будем искать из
требования чтоб
удовлетворяло условиям интерполирования:
в формуле (2) будем искать из
требования чтоб
удовлетворяло условиям интерполирования:
![]() .
Тогда
.
Тогда
![]() (3)
(3)
![]() ,
,
расписав это равенство при
получаем систему из
линейных алгебраических уравнений
(СЛАУ) относительно
![]() неизвестных коэффициентов
неизвестных коэффициентов
![]() .
Матрица системы имеет следующий вид:
.
Матрица системы имеет следующий вид:
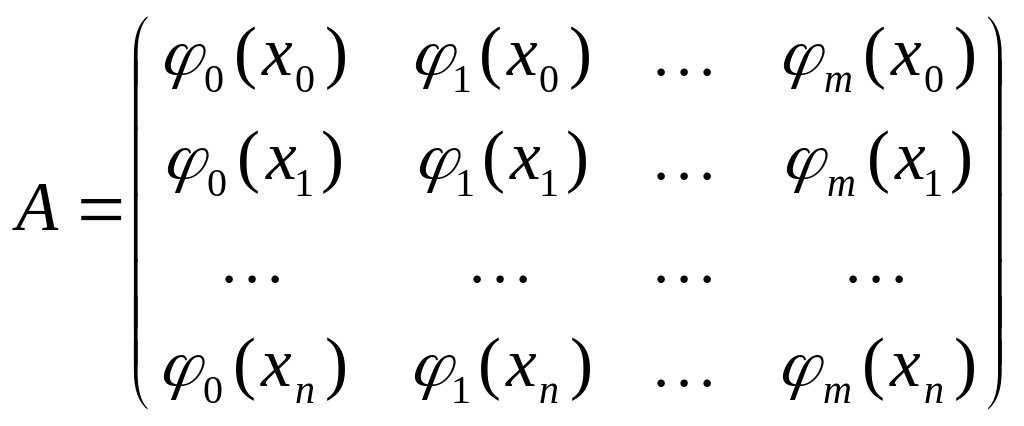 (3`)
(3`)
Выясним вопрос о разрешимости СЛАУ
(3`). На основании теоремы
Кронекера-Капелли решение системы (3`)
существует и единственно тогда и только
тогда, когда
![]() и
и
![]() .
Тогда решив СЛАУ (3`) любым
известным методом находим коэффициенты
.
Тогда решив СЛАУ (3`) любым
известным методом находим коэффициенты
![]() и подставив их в формулу (2) получим
интерполяционную функцию
для исходной функции
.
и подставив их в формулу (2) получим
интерполяционную функцию
для исходной функции
.
Интерполирование алгебраическими многочленами
Интерполирование алгебраическими
многочленами является частным случаем
линейного интерполирования, когда в
качестве системы линейно независимых
функций
![]() в формуле (2) выбирается система
элементарных алгебраических многочленов
в формуле (2) выбирается система
элементарных алгебраических многочленов
![]() .
Тогда интерполирующая функция записывается
в виде:
.
Тогда интерполирующая функция записывается
в виде:
![]() (4)
(4)
Также как и раньше коэффициенты
![]() находят из выполнимости условия
интерполяции:
.
находят из выполнимости условия
интерполяции:
.
Получаем систему вида:
![]() (5).
(5).
Определитель матрицы системы (5) имеет вид:
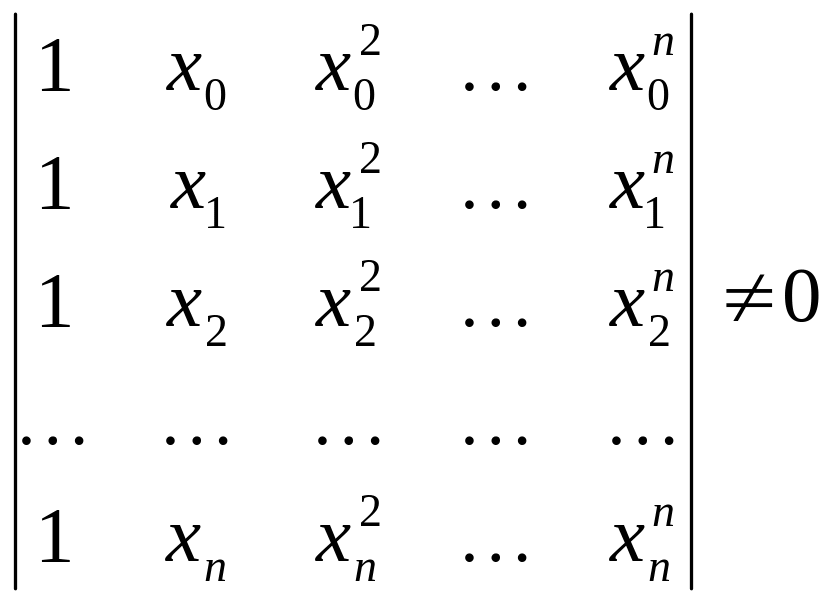 -
определитель Вандермонда.
-
определитель Вандермонда.
Так как определитель
![]() то решение системы (5) существует
и единственно для
то решение системы (5) существует
и единственно для
![]() и
и
![]() .
.
Таким образом, показано существование
и единственность интерполяционного
алгебраического многочлена степени не
выше
![]() (некоторые
могут равняться 0) для любой функции
.
(некоторые
могут равняться 0) для любой функции
.
Замечание. Если количество узлов интерполяции достаточно велико, то построение интерполяционного алгебраического многочлена указанным способом приводит к решению СЛАУ высокого порядка, поэтому укажем другой способ построения интерполяционного многочлена несвязанный с решением системы (5).
Интерполяционный многочлен Лагранжа
Пусть на отрезке
заданы
попарно различных и не обязательно
равноудалённых точек
и
:
.
Для построения для функции
по системе узлов
![]() интерполяционного алгебраического
многочлена решим для начала частичную
подзадачу: для каждого фиксированного
интерполяционного алгебраического
многочлена решим для начала частичную
подзадачу: для каждого фиксированного
![]() построим многочлен
-ой
степени
построим многочлен
-ой
степени
![]() ,
такой что в узлах интерполяции
,
такой что в узлах интерполяции
![]() .
.
То есть в узлах интерполяции
![]() многочлен
многочлен
![]() ,
а в точке
,
а в точке
![]() многочлен
многочлен
![]() .
Тогда легко заметить, что многочлен
.
Тогда легко заметить, что многочлен
![]() (1) будет искомым интерполяционным
многочленом. В самом деле, для указанной
системы узлов
этот многочлен будет иметь степень по
крайней мере
(1) будет искомым интерполяционным
многочленом. В самом деле, для указанной
системы узлов
этот многочлен будет иметь степень по
крайней мере
![]() и будет выполняться условие интерполяции:
и будет выполняться условие интерполяции:
![]() .
.
Так как
многочлен
-ой
степени, а точки
- его корни (
корней), то мы можем разложить его в
произведение:
![]() (2),
(2),
где
![]() найдём из условия, что
.
Получим
найдём из условия, что
.
Получим
![]()
![]() ,
тогда
,
тогда
![]() .
Подставляя в формулу (1) получим
искомый интерполяционный многочлен
Лагранжа:
.
Подставляя в формулу (1) получим
искомый интерполяционный многочлен
Лагранжа:
 (3).
(3).
Перепишем формулу в ином виде. Для этого
введём вспомогательный многочлен
![]() -ой
степени:
-ой
степени:
![]() .
Перепишем (3) в терминах многочлена
.
Перепишем (3) в терминах многочлена
![]() .
Легко видеть, что произведение можно
записать в виде:
.
Легко видеть, что произведение можно
записать в виде:
![]() .
Рассмотрим производную:
.
Рассмотрим производную:
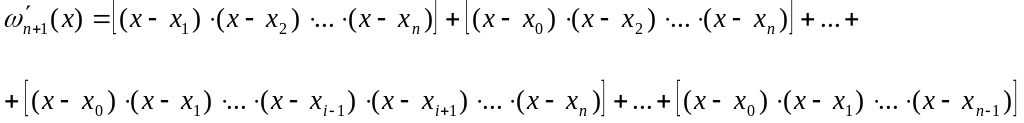
это будет сумма некоторых произведений.
Вычислим производную в точке , получим:
![]() .
.
Подставив в формулу (3) получим:
![]() (4).
(4).
Формула (4) будет использоваться нами в теоретических целях.
Рассмотрим вопрос о погрешности интерполирования при помощи многочлена Лагранжа.
Определение. Остаточным
членом интерполяционного многочлена
Лагранжа называется определённая на
функция
![]() (5).
(5).
Очевидно что в узлах интерполяции
![]() погрешность
погрешность
![]() ,
но нас интересует выражение остаточного
члена для
,
но нас интересует выражение остаточного
члена для
![]() .
.
Теорема. Пусть функция
на
,
содержащем все узлы интерполяции,
непрерывна и имеет непрерывные производные
до
-го
порядка включительно, тогда для
найдётся такая точка
![]() что для остаточного члена
что для остаточного члена
![]() интерполяционного многочлена справедлива
формула:
интерполяционного многочлена справедлива
формула:
![]() ,
,
![]() (6).
(6).
{Доказать самостоятельно}
На практике высшие производные функции
могут оказаться недоступными, кроме
того задача нахождения точки
вызывает затруднения, поэтому если
известна величина
![]() ,
то для остаточного члена может быть
получена следующая оценка:
,
то для остаточного члена может быть
получена следующая оценка:
![]() (7).
(7).
Сходимость процесса интерполяции
Рассмотрим на
следующую совокупность узлов интерполяции
.
Предположим, что имеется один узел при
![]() .
По этому узлу
.
По этому узлу
![]() строим интерполяционный многочлен
Лагранжа
строим интерполяционный многочлен
Лагранжа
![]() .
При
.
При
![]() имеется два узла интерполяции
имеется два узла интерполяции
![]() и
и
![]() по которым строим интерполяционный
многочлен Лагранжа
по которым строим интерполяционный
многочлен Лагранжа
![]() .
.
При
![]() имеется три узла интерполяции
имеется три узла интерполяции
![]() ,
,![]() и
и
![]() по которым строим интерполяционный
многочлен Лагранжа
по которым строим интерполяционный
многочлен Лагранжа
![]() и т.д.
и т.д.
![]()
![]() по которым строим интерполяционный
многочлен Лагранжа
по которым строим интерполяционный
многочлен Лагранжа
![]() .
.
Возникает вопрос будет ли иметь место
сходимость при
![]() .
.
Определение. Будем говорить,
что интерполяционный процесс
![]() для
функции
по системе узлов (треугольная матрица
узлов)
для
функции
по системе узлов (треугольная матрица
узлов)
 сходится для
сходится для
![]() ,
если
,
если
![]() и говорят, что существует поточечная
сходимость. Если же указанная сходимость
имеет место сразу для всех
и она к тому же равномерная, то говорят
о равномерной сходимости интерполяционного
процесса для функции
.
Но равномерная сходимость не всегда
имеет место и процесс интерполяции
является, вообще говоря, расходящимся.
и говорят, что существует поточечная
сходимость. Если же указанная сходимость
имеет место сразу для всех
и она к тому же равномерная, то говорят
о равномерной сходимости интерполяционного
процесса для функции
.
Но равномерная сходимость не всегда
имеет место и процесс интерполяции
является, вообще говоря, расходящимся.
Теорема Фабера. Для любой треугольной матрицы узлов указанного вида найдётся такая непрерывная функция , для которой интерполяционный процесс не будет сходящимся равномерно на .
Теорема Марцинкевича. Для любой непрерывной функции найдётся такая треугольная матрица узлов на , что процесс интерполяции будет равномерно сходящимся для функции всюду на . (Теорема имеет только теоретическое значение).
Существуют классы функций (непрерывно-дифференцируемые, абсолютно-непрерывные) для которых в математической литературе сформулированы признаки равномерной сходимости.
Выбор узлов интерполяции
Пусть функция
задана достаточно обширной таблицей
своих значений на
.
Пусть
- некоторое не табличное значение
аргумента
.
Требуется интерполировать
в точке
при помощи многочлена
-ой
степени взяв в качестве узлов интерполяции
такие
![]() значений, чтобы погрешность интерполяции
в точке
была минимальной.
значений, чтобы погрешность интерполяции
в точке
была минимальной.
Рассмотрим:
, , (6).
Выражение (6) сложно зависит от , поэтому воспользуемся формулой (7):
![]() ,
,
так как
![]() и
и
![]() не зависят от узлов интерполяции, то
не зависят от узлов интерполяции, то
![]() .
.
Естественно выбрать среди всех табличных
значений функции
в качестве узлов интерполяции
те точки, которые являються ближайшими
к точке
.
На основе формулы (7) мы получим
наименьшее возможное значение для
погрешности в точке
.
Если задача состоит в выборе таких
узлов, чтобы погрешность
![]() была минимальной для
была минимальной для
![]() ,
тогда: среди всех алгебраических
многочленов вида
,
тогда: среди всех алгебраических
многочленов вида
![]() ,
корни которых расположены на
найдём такой, для которого величина:
,
корни которых расположены на
найдём такой, для которого величина:
![]() принимает наименьшее значение. Такая
задача решается при помощи многочленов
Чебышева. Если в качестве узлов
интерполяции
на
взять корни многочлена Чебышева
-ой
степени, а именно точки:
принимает наименьшее значение. Такая
задача решается при помощи многочленов
Чебышева. Если в качестве узлов
интерполяции
на
взять корни многочлена Чебышева
-ой
степени, а именно точки:
![]() ,
,
то многочлен
![]() становится многочленом наименее
уклоняющимся от нуля всюду на
и погрешность интерполирования будет
минимальной.
становится многочленом наименее
уклоняющимся от нуля всюду на
и погрешность интерполирования будет
минимальной.
Разделённые разности и их свойства
Пусть на
задано
попарно различных и не обязательно
равноудалённых точек
и известны значения функции
в этих точках:
![]() .
.
Определение. Разделёнными
разностями 1-го порядка функции
называется отношение вида:
![]() .
.
Разделённые разности 1-го порядка имеют
смысл средней скорости роста функции
на промежутке
![]() и являются обобщённым понятием производной
функции.
и являются обобщённым понятием производной
функции.
Разделёнными разностями 2-го
порядка функции
называется отношение вида:
![]() и т.д.
и т.д.
Если известна разделённая разность
функции
![]() -го
порядка, то можно определить разделённую
разность
-го
порядка, то можно определить разделённую
разность
![]() -го
порядка:
-го
порядка:
![]() .
.
Свойства разделенных разностей:
Разделённая разность -го порядка вычисляется через значение функции по следующей формуле:
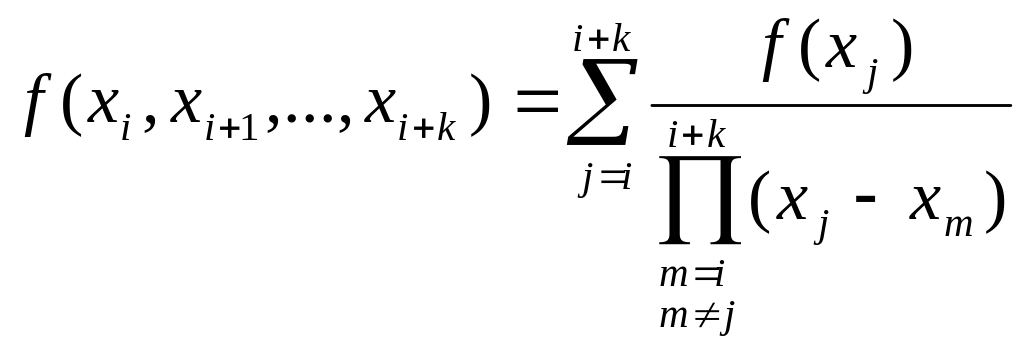 (1).
(1).
Разделённая разность произвольного порядка является линейным оператором функции если она представима в виде:
 ,
где
,
где
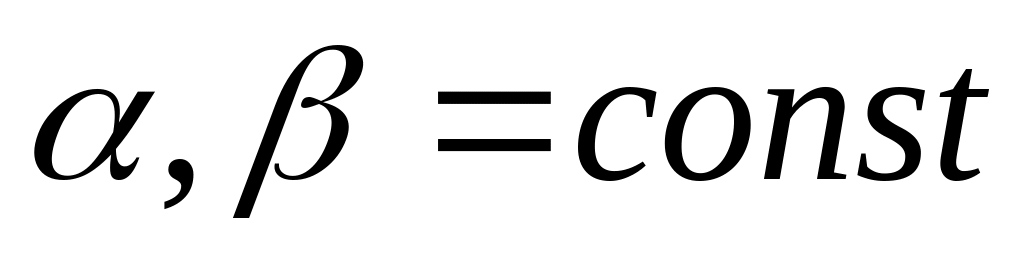 ,
то
,
то
 .
.Разделённая разность произвольного порядка является симметрической функцией своих аргументов, т.е. не меняет свой знак при перестановке аргументов.
Если непрерывна на вмести со своими производными до -го порядка включительно, то найдётся такая точка
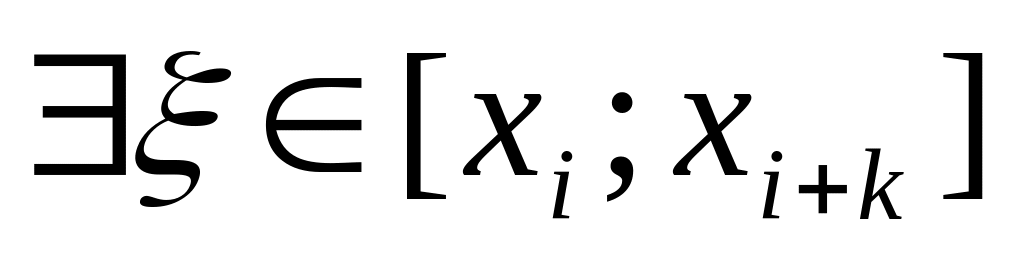 ,
что выполняется равенство:
,
что выполняется равенство:
 (2).
(2).
Следствие. Разделённые разности -го порядка от многочлена степени постоянны, а разделённые разности более высоких порядков многочлена степени равны нулю.
{Доказать самостоятельно}
Интерполяционные многочлены Ньютона в разделённых разностях
Пусть на имеются попарно различных и не обязательно равноудалённых точек и известны значения функции в этих точках: .
Напомним выражение для интерполяционного многочлена Лагранжа функции по заданной системе узлов:
(3).
Рассмотрим для
![]() разность:
разность:

![]() (4).
(4).
(Выражение в [] на основе формулы (1)
будет разделённой разностью
![]() -го
порядка).
-го
порядка).
Зафиксируем целое
![]() и обозначим через
и обозначим через
![]() интерполяционный многочлен Лагранжа
для функции
по узлам
интерполяционный многочлен Лагранжа
для функции
по узлам
![]() .
Из условия интерполяции имеем:
.
Из условия интерполяции имеем:
![]() .
.
Запишем многочлен Лагранжа -ой степени в следующем виде:
![]() (5).
(5).
![]() -многочлен
нулевой степени,
построенный по узлу
-многочлен
нулевой степени,
построенный по узлу
![]() :
:
![]() .
Рассмотрим для произвольного
.
Рассмотрим для произвольного
![]() разность
разность
![]() -
алгебраический многочлен степени
.
Поскольку из условия интерполяции:
-
алгебраический многочлен степени
.
Поскольку из условия интерполяции:
![]()
![]() .
.
То есть указанный алгебраический
многочлен имеет в точках
![]() корни
штук, тогда по известной теореме алгебры:
корни
штук, тогда по известной теореме алгебры:
![]() и в последнем равенстве возьмём
и в последнем равенстве возьмём
![]() ,
тогда получим:
,
тогда получим:
![]() (6).
(6).
Возьмём в формуле (4)
,
![]() ,
получим:
,
получим:
![]() (7).
(7).
Так как левые части выражений (6) и (7) равны, то равны и правые части:
![]() -
разделённая разность
-го
порядка. Тогда зная значение
-
разделённая разность
-го
порядка. Тогда зная значение
![]() можно записать для
можно записать для
![]() :
:
![]() (8).
(8).
С учётом формулы (8) выражение (5) принимает вид:
![]() (9) – интерполяционный
многочлен Ньютона в разделённых разностях
для интерполирования вперёд.
(9) – интерполяционный
многочлен Ньютона в разделённых разностях
для интерполирования вперёд.
Замечание. Если изменить порядок
привлечения узлов интерполяции при
построении формулы Ньютона
![]() ,
то формула (9) принимает вид:
,
то формула (9) принимает вид:
![]() (10) – интерполяционный многочлен
Ньютона в разделённых разностях для
интерполирования назад.
(10) – интерполяционный многочлен
Ньютона в разделённых разностях для
интерполирования назад.
Проведём сравнительный анализ построенных интерполяционных многочленов. Формулы Ньютона (9) и (10) удобные для использования на практике в том случае, если необходимо добавить один или несколько дополнительных узлов интерполяции. В этом случае в формуле (9) или (10) достаточно добавить одно или несколько слагаемых в то время как использование формулы (3) (интерполяционный многочлен Лагранжа) приводит к повторению всей проделанной работы.
С другой стороны, если необходимо интерполировать сразу несколько функций по одной системе узлов, то в этом случае целесообразно использовать формулу (3), так как многочлены могут быть единожды вычислены в указанной точке.
Сравним теперь формулы (9) и (10).
На основании свойства 4 (смотри
формулу (2)) разделённые разности
имеют тенденцию убывать с ростом порядка
(![]() ),
поэтому наибольший вклад в результат
вносят лишь первые слагаемые и если на
практике интересующее нас значение
расположено ближе к началу таблицы
узлов, то целесообразно использовать
формулу (9), она будет точнее.
Если же интересующее нас значение
расположено ближе к концу таблицы узлов,
то целесообразно использовать формулу
(10).
),
поэтому наибольший вклад в результат
вносят лишь первые слагаемые и если на
практике интересующее нас значение
расположено ближе к началу таблицы
узлов, то целесообразно использовать
формулу (9), она будет точнее.
Если же интересующее нас значение
расположено ближе к концу таблицы узлов,
то целесообразно использовать формулу
(10).
Остаточный член интерполяционного многочлена Ньютона в разделённых разностях для интерполирования вперёд
Пусть
![]() ,
тогда на основе формулы (4) имеем:
,
тогда на основе формулы (4) имеем:
![]() (11).
(11).
Формулой (11) для остаточного
члена на практике пользоваться тяжело
из-за того, что
![]() на основе свойства 1 разделённых
разностей зависит от
,
а
может быть неизвестна. Приведём формулу
приближенного вычисления погрешности
интерполирования. Предположим, что нам
известно дополнительное значение
функции
ещё в одной точке
на основе свойства 1 разделённых
разностей зависит от
,
а
может быть неизвестна. Приведём формулу
приближенного вычисления погрешности
интерполирования. Предположим, что нам
известно дополнительное значение
функции
ещё в одной точке
![]() ,
а так же известно, что производная
,
а так же известно, что производная
![]() ,
а значит и разделённая разность
-го
порядка на
изменяются несущественно. Тогда вместо
интересующего нас значения аргумента
в разделённую разность можно подставить
,
а значит и разделённая разность
-го
порядка на
изменяются несущественно. Тогда вместо
интересующего нас значения аргумента
в разделённую разность можно подставить
![]() ,тогда
получим:
,тогда
получим:
![]() (12).
(12).
Конечные разности и их свойства
Рассмотрим на
совокупность равноотстоящих с шагом
![]() точек
,
то есть
точек
,
то есть
![]() .
.
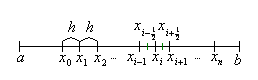
Легко видеть, что каждую точку можно
найти по формуле:
![]() ,
а величина шага может быть вычислена
по формуле:
,
а величина шага может быть вычислена
по формуле:
![]() .
.
Пусть известны значения некоторой
функции
в этих точках:
![]() .
.
Определим так же следующие точки
![]() и
и
![]() (значение
(значение
![]() может быть дробным).
может быть дробным).
Будем считать, что известны значения и
в этих точках:
![]() .
.
Определение. Конечными разностями 1-го порядка функции в точке называется следующие величины:
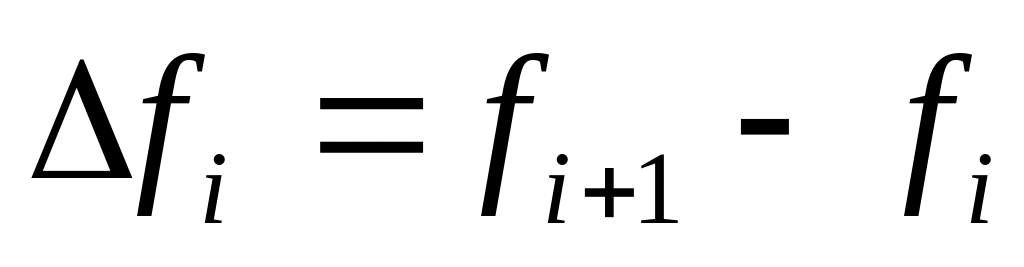 -
правые конечные разности
-
правые конечные разности
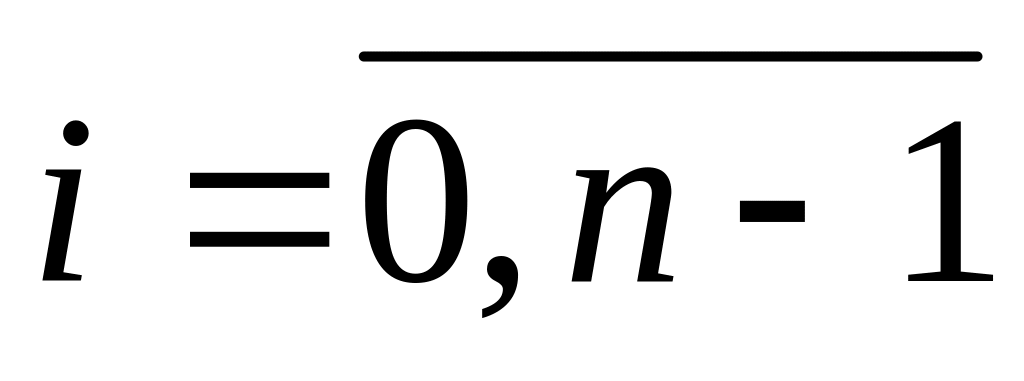 ,
, -
левые конечные разности
-
левые конечные разности
 ,
,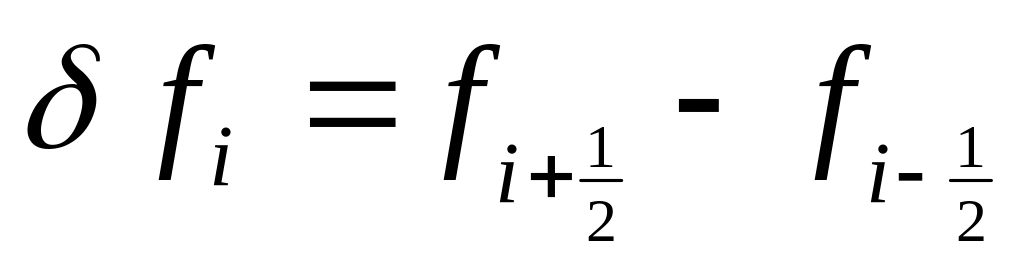 -
центральные конечные разности.
-
центральные конечные разности.
Легко видеть, что конечные разности
1-го порядка связаны между собой следующим
образом:
![]() .
.
Определение. Конечные разности более высоких порядков для функции в точке определяются следующим образом:
 ,
, ,
,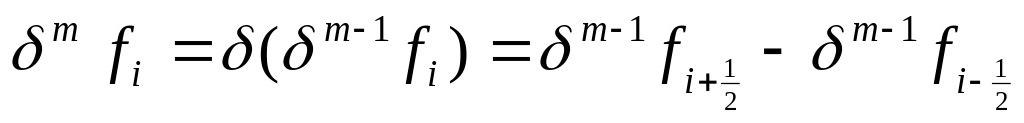 .
.
Существует также связь и между конечными разностями высоких порядков:
![]() (1).
(1).
Свойства конечных разностей:
Конечная разность произвольного порядка выражается через значение функции по следующей формуле:
 (2),
где
(2),
где
 .
.Конечная разность произвольного порядка является линейным оператором функции . То есть если функция представима в виде
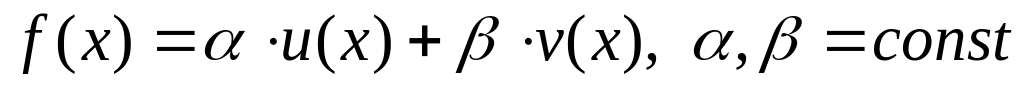 ,
то и конечные разности можно записать
в виде
,
то и конечные разности можно записать
в виде
 .
.Связь между конечными и разделёнными разностями:
![]() (3).
(3).
Если непрерывна на вместе со своими производными до -го порядка включительно, то
 ,
такая что справедливо следующее
равенство:
,
такая что справедливо следующее
равенство:
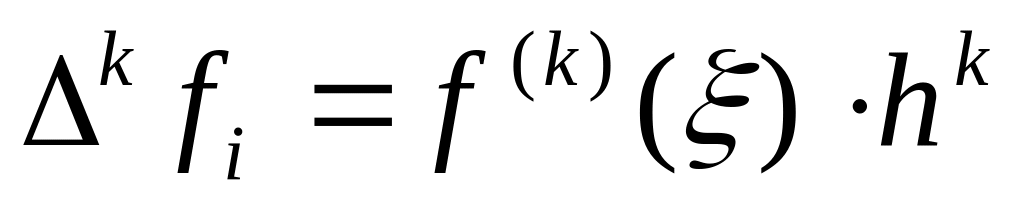 (4).
(4).
Следствие. Конечные разности -го порядка для многочлена степени постоянны, а конечные разности более высоких порядков равны нулю.
Интерполяционные многочлены Ньютона в конечных разностях
Пусть на
заданы
равноудалённых точек
с шагом
и известны значения функции
в этих точках:
![]() .
.
Естественно ожидать, что интерполяционные формулы Ньютона существенно упростятся в случае равноотстоящих узлов.
Запишем интерполяционный многочлен Ньютона в разделённых разностях для интерполирования вперёд:
(5),
а также формулу, которая связывает между собой разделённые и конечные разности: .
Теперь преобразуем формулу (5)
используя формулу (3) (свойство
3 конечных разностей), а также учитывая
то, что
![]() .
Выполнив в формуле (5) замену
переменной:
.
Выполнив в формуле (5) замену
переменной:
![]() ,
получим:
,
получим:
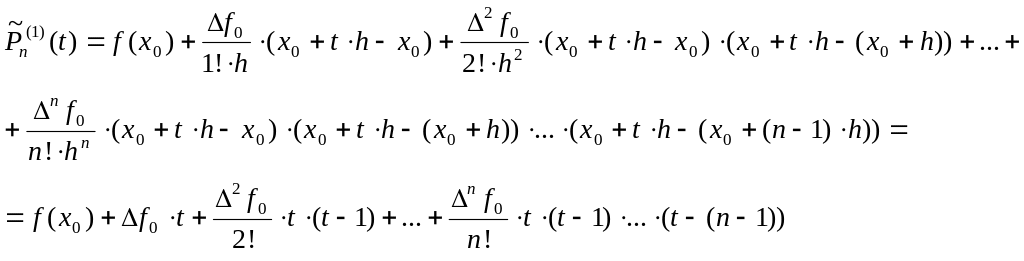 (6)
–
(6)
–
интерполяционный многочлен Ньютона в конечных разностях для интерполирования вперёд.
Аналогично можно преобразовать формулу Ньютона для интерполирования назад.
(7).
Используя свойство 3 конечных
разностей, далее можно установить, что
равноотстоящие узлы
подчиняются следующей формуле:![]() .
Выполнив в формуле (7) замену:
.
Выполнив в формуле (7) замену:
![]() ,
получим:
,
получим:
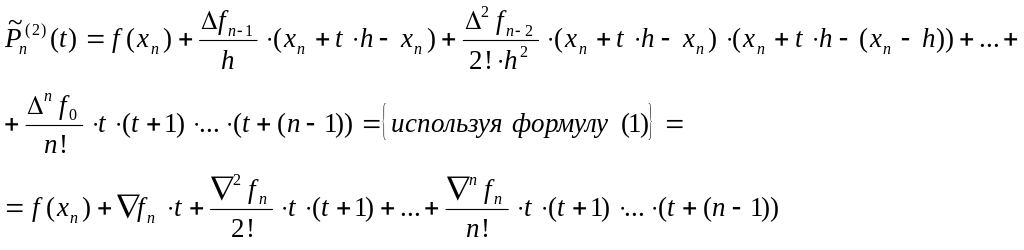 (8)
–
(8)
–
интерполяционный многочлен Ньютона в конечных разностях для интерполирования назад.
Рассмотрим вопрос о погрешности формул (6) и (8).
Воспользуемся формулой остаточного члена интерполяционного многочлена Лагранжа: , (9).
Предположим, что нам известно значения
функции
в точке
(имеется ещё одно дополнительное
табличное значение) и
(а значит и конечные разности
-го
порядка) на
меняется несущественно. Тогда на
основании свойства 4 конечных
разностей, получим:
![]() .
Выполним в формуле (9) замену:
.
Выполним в формуле (9) замену:
![]() .
Получим приближённое выражение для
остаточного члена формулы (6):
.
Получим приближённое выражение для
остаточного члена формулы (6):
![]() (10).
(10).
{ Самостоятельно получить выражение для приближенного значения погрешности формулы (8)}
Среднеквадратическое приближение функций
Известно, что при интерполировании функции на отрезке с увеличением количества узлов интерполяции растёт и степень интерполяционного многочлена, а это не всегда приводит к улучшению качества приближения.
В связи с этим возникает задача о таком приближении функции на , которое характеризовало бы функцию на рассматриваемом отрезке в целом и не обязательно совпадало с ней в заданных точках.
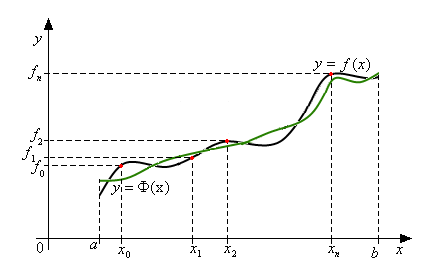
Задача среднеквадратического приближения
состоит в том, что требуется для функции
на
построить такую аппроксимирующую
(approximate – приближать) функцию
![]() ,
которая доставляла бы интегралу
,
которая доставляла бы интегралу
![]() (1) по возможности малое значение.
(1) по возможности малое значение.
Малость интеграла (1) означает,
что на подавляющей части отрезка
функции
и
близки друг к другу, хотя в отдельных
точках отрезка разность
![]() может быть велика.
может быть велика.
Величина
 (2) называется среднеквадратическим
уклонением функции
от
и характеризирует погрешность приближения
функции
при помощи
в смысле среднеквадратического.
(2) называется среднеквадратическим
уклонением функции
от
и характеризирует погрешность приближения
функции
при помощи
в смысле среднеквадратического.
Если аналитическое представление
функции
неизвестно, а функция задана лишь своими
значениями в
точках
![]() ,
то тога вместо интеграла (1)
естественно рассматривать суммы вида:
,
то тога вместо интеграла (1)
естественно рассматривать суммы вида:
![]() (3),
а вместо среднеквадратического отклонения
(2) выражение вида:
(3),
а вместо среднеквадратического отклонения
(2) выражение вида:
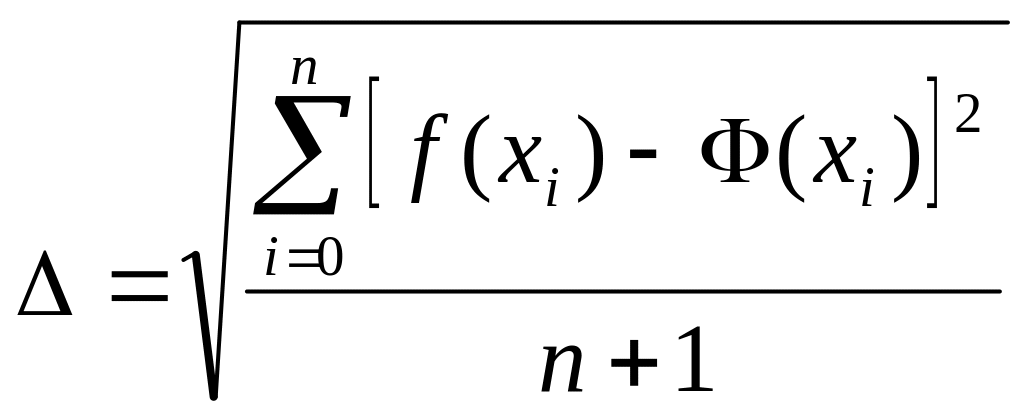 (4).
(4).
В качестве аппроксимирующей функции чаще всего используются алгебраические или тригонометрические многочлены.
Метод наименьших квадратов (МНК) для функции заданной таблично (дискретный случай)
Пусть на имеется совокупность попарно различных и не обязательно равноотстоящих точек и пусть известны значения некоторой функции в этих точках, такие что .
Требуется среди всех алгебраических
многочленов степени
![]() следующего вида
следующего вида
![]() (1) найти такой, который доставлял
бы минимальное значение следующей
сумме:
(1) найти такой, который доставлял
бы минимальное значение следующей
сумме:
![]() (2).
(2).
На величину
![]() можно смотреть как на неотрицательную
функцию многих переменных, а именно
:
можно смотреть как на неотрицательную
функцию многих переменных, а именно
:
![]() .
.
Для того чтоб найти значения коэффициентов
при которых функция
достигает своей точной нижней грани
![]() воспользуемся необходимым условием
минимума (все частные производные
функции равны нулю):
воспользуемся необходимым условием
минимума (все частные производные
функции равны нулю):
![]() .
Рассмотрим:
.
Рассмотрим:

Система равенств (3) представляет собой СЛАУ относительно неизвестных коэффициентов .
Эта СЛАУ имеет уравнение и неизвестную.
Введём следующее обозначение:
![]() и
и
![]() .
.
Тогда получим:
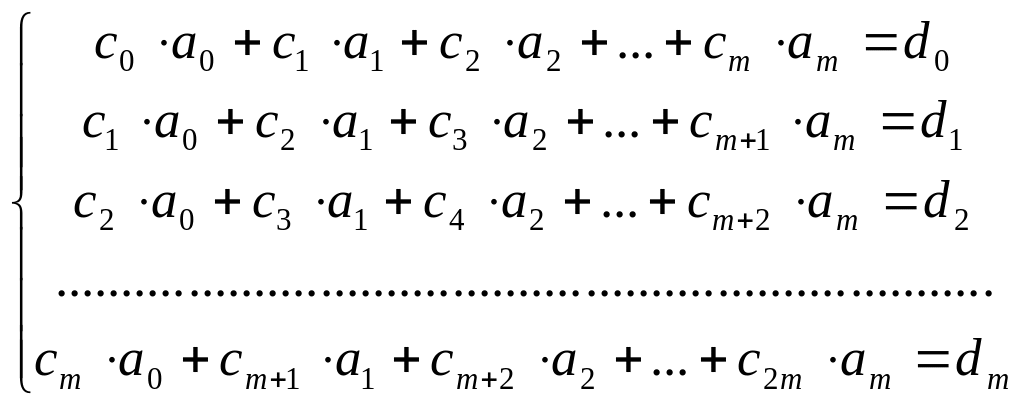 (3`).
(3`).
Матрица СЛАУ (3`) носит название
матрицы Грамма системы линейно независимых
элементов
![]() .
Эта матрица является симметричной и
невырожденной
.
Эта матрица является симметричной и
невырожденной
![]() ,
следовательно существует единственное
решение системы (3)
,
следовательно существует единственное
решение системы (3)
![]() ,
которое доставляет минимум выражению
вида (2). Найдя решение СЛАУ (3)
любым известным методом и подставив
его в формулу (1) получим искомый
многочлен степени
,
дающий наилучшее среднеквадратическое
приближение функции
заданной таблично.
,
которое доставляет минимум выражению
вида (2). Найдя решение СЛАУ (3)
любым известным методом и подставив
его в формулу (1) получим искомый
многочлен степени
,
дающий наилучшее среднеквадратическое
приближение функции
заданной таблично.
Замечание 1. Если
,
то в этом случае многочлен наилучшего
среднеквадратического приближения
![]() для функции
заданной таблично совпадает с
интерполяционным многочленом
,
поскольку требование
приводит нас к следующим условиям:
для функции
заданной таблично совпадает с
интерполяционным многочленом
,
поскольку требование
приводит нас к следующим условиям:
![]() ,
что приводит нас к условию интерполирования.
,
что приводит нас к условию интерполирования.
Замечание 2. Если известно
аналитическое значение
на
,
то в этом случае требуется построить
такой алгебраический многочлен
![]() ,
который при данном
доставлял бы минимальное значение
интегралу
,
который при данном
доставлял бы минимальное значение
интегралу
![]() и в этом случае схема метода наименьших
квадратов, рассмотренная выше, полностью
распространяется и на этот случай с
единственным отличаем в формулах:
и в этом случае схема метода наименьших
квадратов, рассмотренная выше, полностью
распространяется и на этот случай с
единственным отличаем в формулах:
![]() и
и
![]() ,
где в качестве линейно независимых
элементов выступают
,
где в качестве линейно независимых
элементов выступают
![]() .
.
Численное интегрирование
Постановка задачи
Под численным интегрированием понимают приближённое вычисление интеграла, если подынтегральная функция имеет сложное аналитическое выражение или задана таблично, то точные методы интегрирования, изученные в математическом анализе, становятся неприменимыми. Для таких интегралов разработаны приближённые способы вычисления.
Формулы приближённого вычисления интегралов называются квадратурными формулами. Основная идея построения этих формул основана на замене подынтегральной функции приближающей функцией интеграл от которой легко вычислить.
Простейшие квадратурные формулы могут быть получены из геометрических соображений.
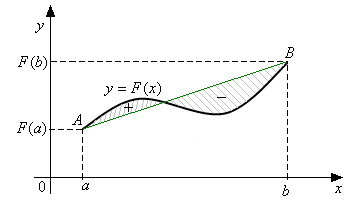
Если заменить участок кривой
примой
![]() ,
где
,
где
![]() и
и
![]() ,
то получим:
,
то получим:
![]() - квадратурная формула трапеций.
- квадратурная формула трапеций.
Всякую квадратурную формулу можно
записать в следующем наиболее общем
виде:
![]() (1), где
(1), где
![]() коэффициенты квадратурной формулы;
коэффициенты квадратурной формулы;
![]() узлы квадратурной формулы;
узлы квадратурной формулы;
![]() погрешность, остаточный член квадратурной
формулы;
погрешность, остаточный член квадратурной
формулы;
![]() целое число, которое выбирается из
соображений точности;
целое число, которое выбирается из
соображений точности;
![]() весовая функция;
известная подынтегральная функция.
весовая функция;
известная подынтегральная функция.
Разные квадратурные формулы отличаются друг от друга способом выбора узлов и коэффициентов.
Определение. Говорят, что
квадратурная формула (1) является
точной, если
![]() .
.
В общем же случае это не так и квадратурную
формулу (1) часто записывают в
следующем виде:
![]() (2).
(2).
Большинство квадратурных формул основаны на приближённой замене подынтегральной функции алгебраическим многочленом. В связи с этим возникает понятие алгебраической степени точности квадратурной формулы.
Говорят, что квадратурная формула (1) имеет алгебраическую степень точности если она точна ( ) для всех алгебраических многочленов степени и не является точной хотя бы для одного алгебраического многочлена степени .
Замечание 1. На основе теоремы Вейерштрасса любую непрерывную функцию на конечном отрезке можно сколь угодно точно приблизить алгебраическим многочленом (за счёт увеличения степени многочлена). Поэтому следует ожидать, что чем выше алгебраическая степень точности квадратурной формулы, то тем более точный результат она будет давать на классе непрерывных функций.
Замечание 2. Если квадратурная
формула точна для всех алгебраических
многочленов степени
,
то она будет точна и для всех алгебраических
многочленов степени
![]() .
.
Интерполяционные квадратурные формулы
Построение этих формул основано на замене подынтегральной функции ее интерполяционным многочленом.
Выберем на отрезке интегрирования
совокупность попарно различных узлов
интерполяции:
узел
и представим подынтегральную функцию
в виде суммы:
![]() .
.
В качестве интерполяционного многочлена будем рассматривать интерполяционный многочлен Лагранжа:

,
![]()
тогда
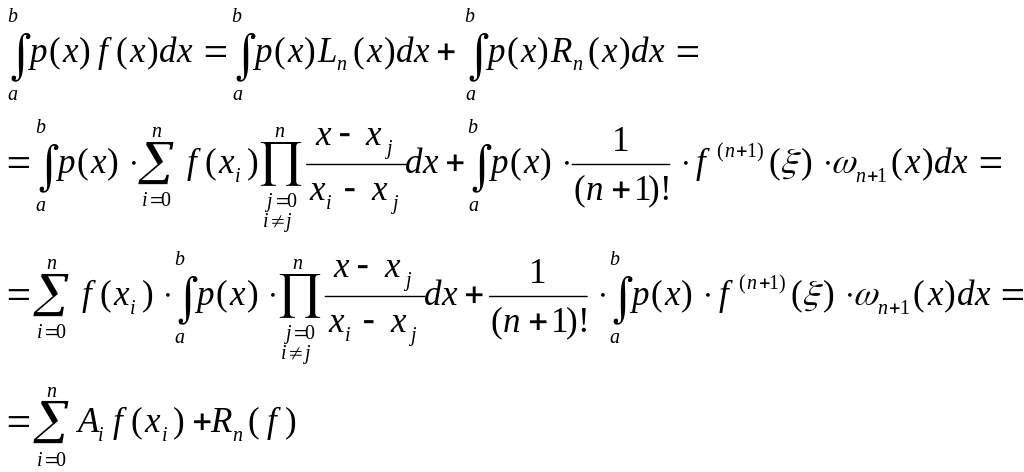 (3).
(3).
где
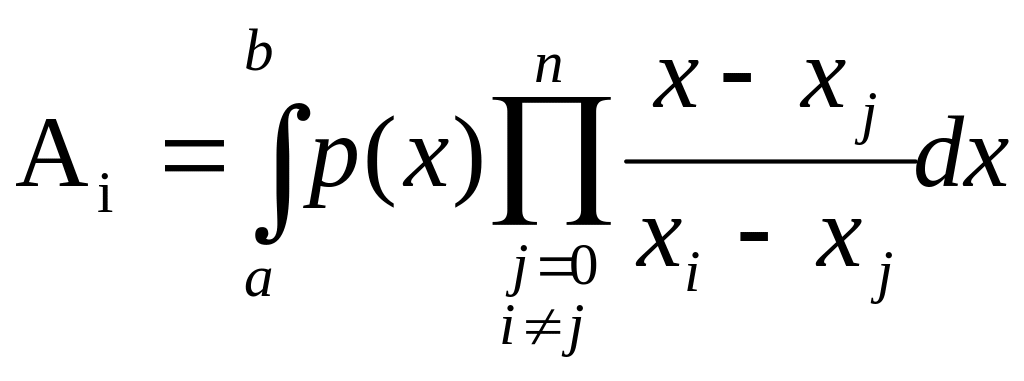 ,
,
![]() (4)
(4)
![]() (5).
(5).
Квадратурная формула (3) называется интерполяционной квадратурной формулой. Её узлы совпадают с узлами интерполяции, а коэффициенты вычисляются по формуле (4).
Теорема (об интерполяционных квадратурных формулах). Для того чтобы квадратурная формула (1) была точна для любого алгебраического многочлена степени необходимо и достаточно чтобы она была интерполяционной.
Замечание. Из этой теоремы следует, что алгебраическая степень точности интерполяционных квадратурных формул равна, по меньшей мере, .
Рассмотрим вопрос об оценке погрешности (5) интерполяционной квадратурной формулы.
Предположим, что в квадратурной формуле
(1) подынтегральная функция
и ее производные непрерывны (производные
до
-го
порядка включительно) на
и пусть:
![]() .
Тогда из (5) получим:
.
Тогда из (5) получим:
![]() (6).
(6).
Заметим, что если функция
![]() изменяет свой знак на
,
то оценка (6) для погрешности может
быть сильно завышенной.
изменяет свой знак на
,
то оценка (6) для погрешности может
быть сильно завышенной.
