Тема 2: середні величини та особливості їх розрахунку

ІНФОРМАЦІЯ

Статистичні показники можуть бути абсолютними, відносними та середніми величинами.

Абсолютні статистичні величини – це кількісні показники, які характеризують розміри суспільних явищ у певних умовах місця і часу.

Відносними статистичними величинами називають показники, які виражають кількісні співвідношення абсолютних показників або співвідношення між явищами суспільного життя.

Середні величини — це узагальнюючі характеристики сукупності подібних (однотипних) одиниць за певною кількісною ознакою, які показують те спільне, характерне, що об'єднує всю масу елементів (тобто статистичну сукупність). Середня величина характеризує типовий рівень ознаки, що варіює, в розрахунку на одиницю статистичної сукупності.

У статистиці застосовують різні види середніх величин: середню арифметичну, середню гармонічну, середню геометричну, середню квадратичну, середню кубічну, структурні середні та ін.

Найбільш поширеним видом середніх вели­чин є середня арифметична. Вона буває простою і зваженою. Середню арифметичну просту застосовують тоді, коли розрахунок здійснюють на основі первинних, не згрупованих даних. Її визначають за формулою:

де - середнє значення ознаки; х_і – окремі значення ознаки (варіанти); п - кількість варіантів (ознак).

Середню арифметичну зважену використовують за згрупованими даними, коли знаменник дробу логічної формули відомий, а чисельник – ні.

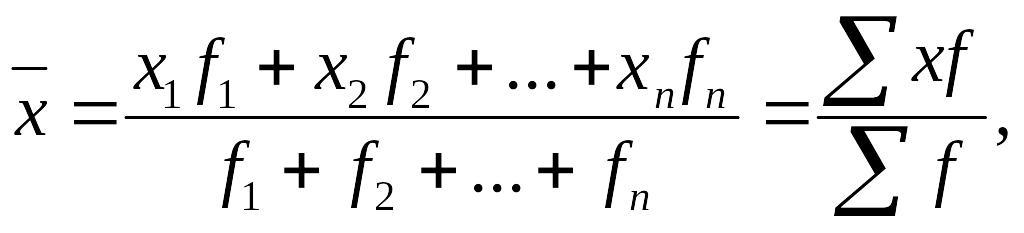
де х — окремі значення ознаки; f -частоти (ваги).

Наступним видом середніх величин є середня гармонічна - це обернена величина до середньої арифметичної. Вона також буває простою і зваженою. Формула середньої гармонічної простої має наступний вигляд:

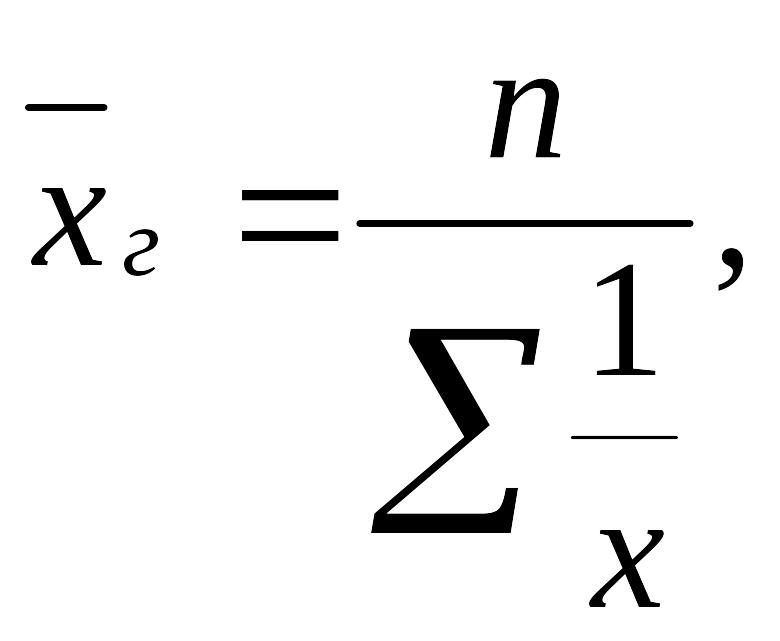
де х — варіанти; п — кількість варіантів.

Формула середньої гармонічної зваженої:

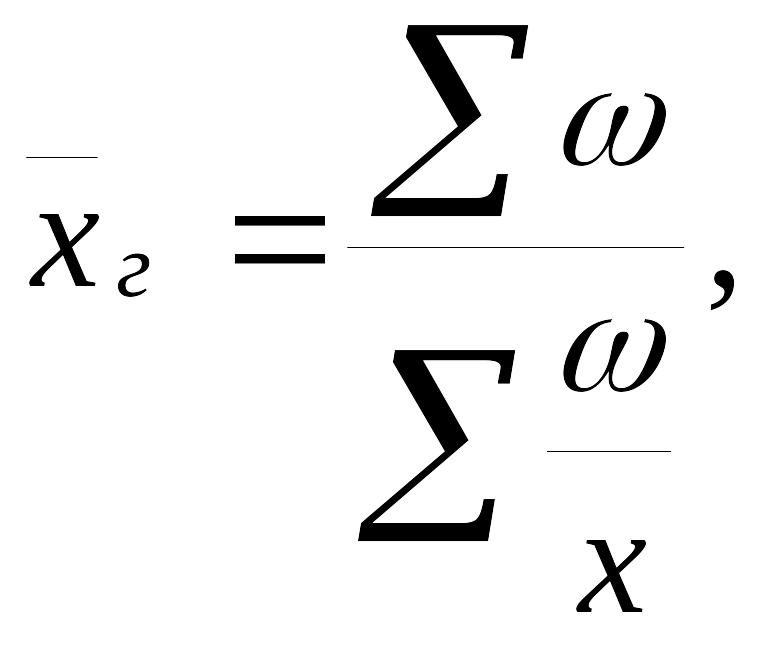
де ω – обсяги явищ.

Середня хронологічна використовується при обрахунках середнього рівня показника на певну дату:

,

де х_1, х_2, х_3, х_п - окремі значення ознаки на певну дату періоду; п- кількість досліджуваних періодів.

Незважаючи на велику кількість видів середніх величин, тільки правильний вибір одного виду середньої для проведення розрахунків, дасть достовірний і істинний результат. Вибір виду середньої величини залежить від характеру вихідних даних.

Для характеристики статистичної сукупності широко використовуються структурні середні, такі як мода та медіана.

Мода (Мо) – значення ознаки (варіанта), що найчастіше зустрічається (повторюється) у сукупності. Коли в ряду розподілу два варіанти мають найбільші і однакові частоти, то такий ряд має дві моди, а розподіл називають бімодальним. Обчислення моди залежить від того, яким рядом розподілу представлені дані статистичної сукупності. Так, якщо дані статистичної сукупності представлені у вигляді дискретного ряду розподілу, мода визначається як варіанта ознаки, що зустрічається найбільшу кількість раз у ряді розподілу. У випадку, коли дані представляються у вигляді інтервального ряду розподілу, мода визначається за допомогою формули:

х_мo - мода; x₀ –нижня межа модального інтервалу; h – величина модального інтервалу; f_mo –частота модального інтервалу; f_mo-1 – частота інтервалу перед модальним; f_mo+1 –частота інтервалу після модального.

Медіана (Ме) – величина ознаки, що займає середнє положення в ряді показників. Тобто це такий розмір явища, який ділить ряд розподілу пополам. Мода медіана визначається в залежності від типу представлення вихідних даних: у дискретному ряді розподілу медіана визначається на основі кумулятивних (нагромаджених) частот. Медіаною буде значення ознаки, кумулятивна частота якої більша за половину обсягу сукупності.

В інтервальному ряді розподілі медіану визначають за формулою:

, де

х_ме –медіана; х₀ –нижня межа медіанного інтервалу; h- величина медіанного інтервалу; f- частоти; S_ме-1 - сума нагромаджених частот перед медіанним інтервалом;f_me - частота медіанного інтервалу.