Тема 7: кореляційний аналіз

ІНФОРМАЦІЯ

Досліджуючи зв’язки між ознаками, виділяють два види зв’язків: функціональний (повний) і кореляційний.

Функціональним називають такий зв'язок між ознаками, при якому кожному значенню однієї змінної (аргументу) відповідає строго визначене значення другої змінної (функції). Такі зв’язки спостерігаються в математиці, фізиці, хімії, астрономії та інших науках.

У соціально-економічних явищах частіше спостерігаються такі зв’язки між змінними величинами, при яких числовому значенню однієї з них відповідає кілька значень інших. Такий зв'язок між ознаками дістав назву кореляційного зв’язку. Прикладом кореляційного зв’язку в сільсько­гос­по­дар­ському виробництві може бути зв'язок між продуктивністю тварин і рівнем годівлі, якістю кормів, породністю худоби; між стажем роботи і продуктивністю праці робітників тощо.

Кореляційний аналіз - це метод визначення і кількісної оцінки взаємозалежностей між статистичними ознаками, що характеризують окремі соціально-економічні явища і процеси. За допомогою кореляційного аналізу вирішують два основні завдання:

1) визначення форми і параметрів рівняння зв’язку;

2) вимірювання тісноти зв’язку.

Перше завдання вирішують, знаходячи рівняння зв’язку і його параметри; друге – обчислюючи різні показники тісноти зв’язку (коефіцієнт кореляції).

Кореляційний зв'язок виражається відповідними математичними рівняннями. Розрізняють прямолінійний і криволінійний, прямий і обернений, парний (визначення зв’язків між двома ознаками) і непарний (визначення взаємозв’язків між трьома і більшою кількістю ознак) кореляційні зв’язки.

При прямому зв’язку зміна факторної ознаки зумовлює зміну результативної ознаки в тому самому напрямку. Якщо ж із збільшенням факторної ознаки результативна ознака зменшується, чи навпаки, то такий зв'язок називають оберненим.

За формою зв’язку розрізняють прямолінійні і криволінійні кореляційні залежності. Прямолінійний кореляційний зв'язок характеризується рівномірним зростанням або зменшенням результативної ознаки під впливом відповідної зміни факторної ознаки. Аналітично його визначають за рівнянням прямої лінії.

При криволінійному кореляційному зв’язку однаковим змінам середніх значень факторної ознаки відповідають різні зміни середніх значень результативної ознаки. Аналітично криволінійний зв'язок визначають за рівнянням кривої лінії.

Залежно від кількості досліджуваних ознак розрізняють парну (просту) і множинну кореляцію. При парній кореляції аналізують зв'язок між факторною і результативною ознаками; при множинній – залежність результативної ознаки від двох і більше факторних ознак.

Залежно від форми зв'язку між факторною і результативною ознаками вибирають тип математичного рівняння. Вибір рівняння для вивчення зв’язків між ознаками є відповідальним завданням, від якого залежать результати кореляційного аналізу. При парній кореляції математичне рівняння встановлюють завдяки побудові графіків (кореляційного поля). При побудові цього графіка на осі абсцис відкладають значення факторної ознаки (Х), а на ординат – значення результативної ознаки (У). Відклавши на перетині відповідних значень Х і У точки, дістають кореляційне поле. За характером розміщення точок на кореляційному полі роблять висновок про напрям і форму зв’язку. Якщо точки безладно розміщені по всьому полю, то залежності між досліджуваними ознаками немає. Якщо ж точки концент­руються навколо уявної осі, направленої від нижнього лівого кута до верхнього правого, то зв'язок між результативною і факторною ознакою прямий. Коли ж точки концентруються навколо уявної осі, направленої з верхнього лівого кута до нижнього правого, то існує обернений зв'язок між ознаками.

Залежно від вихідних даних теоретичною лінією регресії є різні типи кривих або пряма лінія. Так, якщо зміна результативної ознаки під впливом фактора характеризується постійними приростами, це свідчить про лінійний характер зв’язку; якщо ж зміни результативної ознаки під впливом фактора характеризується постійними коефіцієнтами зростання – про криволінійний зв'язок.

Прямолінійну форму зв'язку визначають за рівнянням прямої лінії:

= a₀ +a₁x,

де — теоретичні (обчислені за рівнянням регресії) значення резуль­тативної ознаки;

а₀ – початок відліку, або значення при умові, що х = 0 (економічного змісту немає);

а₁ — коефіцієнт регресії (коефіцієнт пропорційності), який показує, як змінюється при кожній зміні х на одиницю;

х – значення факторної ознаки.

Коефіцієнти регресії є величинами іменованими і мають одиниці вимірювання, що відповідають змінним, зв'язок між якими вони характеризують.

При прямому зв'язку між корелюючими ознаками знак коефіцієнту регресії матиме додатнє значення, а при зворотному - від'ємне (якщо додатнє, то залежність пряма (збільшення Х призводить до збільшення У); якщо ж - від’ємне, то залежність між факторами обернена (збільшення Х призводить до зменшення У). Якщо =0, то значення Х на У не впливає).

Параметри а₀ і а₁ рівняння регресії обчислюють способом наймен­ших квадратів. Суть цього способу полягає в знаходженні таких параметрів рівняння зв'язку, при яких залишкова сума квадратів відхилень фактичних значень результативної ознаки (у) від її теоретичних (об­числених за рівнянням зв'язку) значень ( ) буде мінімальною: ∑ (у — )² = тіп.

Спосіб найменших квадратів зводиться до складання і розв'язан­ня системи двох рівнянь з двома невідомими:

∑ у = па₀ + а₁∑х;

∑ хy = а_о ∑х + а₁ ∑х²,

де п — кількість спостережень.

Розв'язавши цю систему рівнянь у загальному вигляді, матимемо формули для визначення параметрів а_а і а₁:

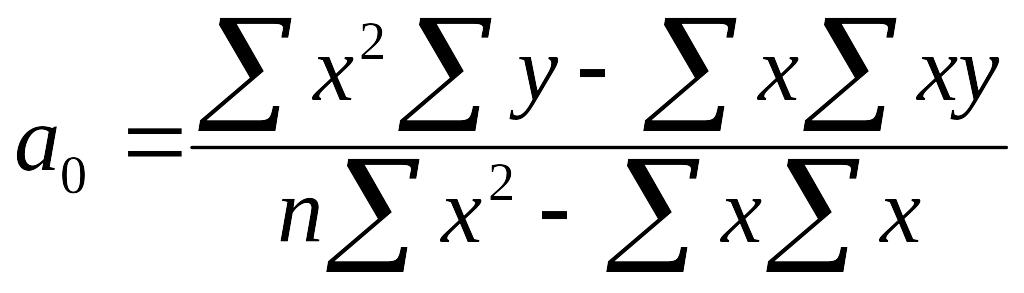
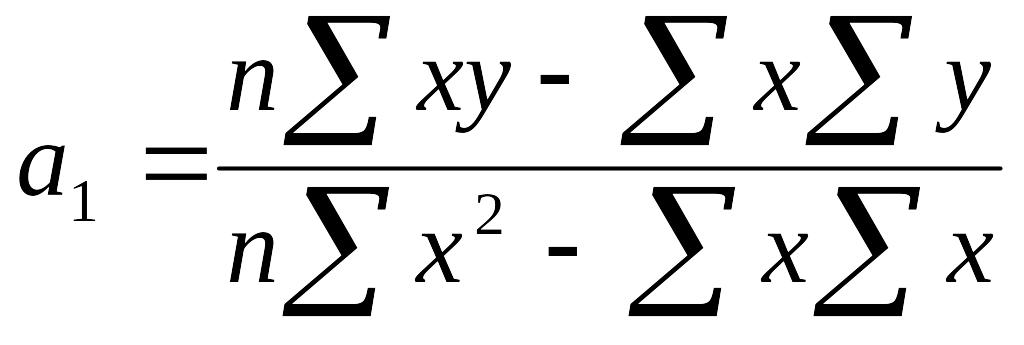
Дослідження форми зв’язку інколи зумовлює потребу в застосуванні нелінійних рівнянь регресії. При криволінійній залежності систему рівнянь будують так, як і для лінійної залежності. Система рівнянь для параболи другого порядку має такий вигляд:

Іноді залежність між корелюючими величинами має гіперболічний характер, тому її встановлюють за допомогою рівняння гіперболи:

При цьому розв’язують таку систему рівнянь з двома невідомими:

Важливим завданням кореляційного аналізу є визначення тісно­ти зв'язку між корелюючими величинами. Кількісним показником тісноти прямолінійного зв'язку результату з одним фактором є кое­фіцієнт парної кореляції, який обчислюють за формулою:

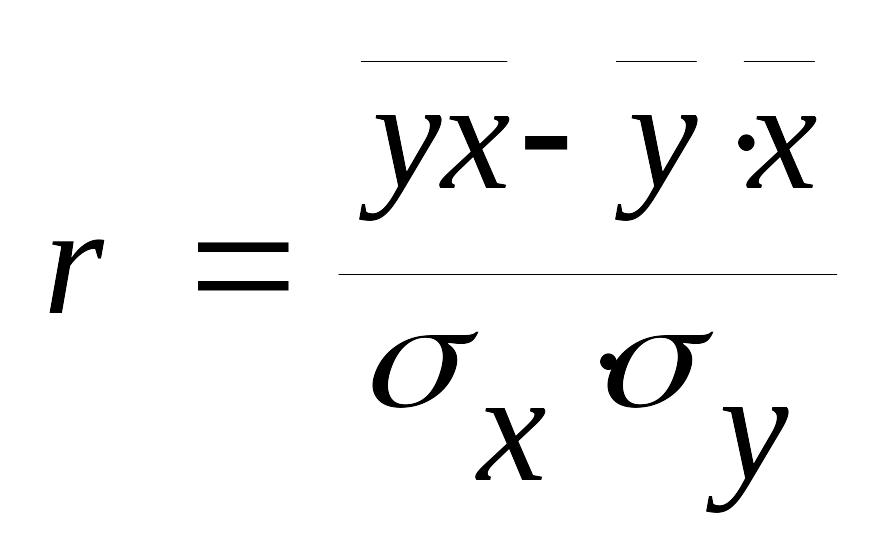
де r — лінійний коефіцієнт парної кореляції; — середнє квадратичне відхилення факторної ознаки; — середнє квадратичне відхилення результативної ознаки.

Якщо врахувати, що , а ; то найбільш зручною формулою для визначення лінійного коефіцієнта, кореляції є:

При парній залежності коефіцієнт кореляції коливається від 0 до +1 при прямому зв'язку та від 0 до – 1 – при зворотному зв'язку. Чим ближче коефіцієнт кореляції до ± 1, тим тісніший зв'язок між У і Х і, навпаки, чим ближче коефіцієнт кореляції до 0, тим слабший зв'язок між результативною і факторною ознаками.

Якщо r < 0,3, то зв'язку немає, якщо r = 0,3–0,5 — зв'язок слабкий, якщо r= 0,5 – 0,7 – зв'язок середній і якщо r>0,7 – зв'язок тісний.

Коефіцієнт кореляції має такий самий знак, як і коефіцієнт регресії у рів­нянні зв'язку.