4.9. Адаптация эконометрических моделей

Адаптация эконометрической модели – это процесс её корректировки на основе вновь поступающей информации, то есть, процесс приспособления ее, к изменившимся условиям формирования моделируемого явления. Адаптация направлена на повышение адекватности модели путём использования текущих новых значений признаков, не известных при её построении.

Можно выделить пространственную и временную адаптацию.

При пространственной адаптации после построения модели множественной регрессии продолжается процесс наблюдения и получения новых данных, на основе корректируются параметры модели.

При временной адаптации используется сдвиг данных, то есть при получении новых данных исключается из рассмотрения часть первоначальных данных, в результате чего модель адаптируется к изменившимся условиям формирования исследуемого явления.

Дополнительным методом временной адаптации является присвоение новым данным больших весов при этом сумма весов, как правило, равна 1.

Рассмотрим адаптацию с использованием разных весов, присваиваемых различным данным. В принципе, веса можно присваивать исходя из предпочтений исследователя, однако разработан ряд специальных методов. Рассмотрим наиболее простой из них – метод гармонических весов.

При использовании этого метода производится сглаживание с помощью метода скользящих трендов, более поздним данным присваиваются большие веса, которые рассчитываются определённым образом, вычисляется средний взвешенный прирост, который используется для прогнозирования следующего уровня динамического ряда. Алгоритм метода может быть представлен следующим образом.

1. Производится сглаживание методом скользящих трендов.

Выбирается число последовательных точек наблюдения для построения скользящих трендов . Обычно

Тренды описываются выражением , , где - общее число точек наблюдения. Параметры трендов определяются с помощью МНК.

2. Определяются средние расчетные значения уровней ряда на основе уравнений трендов.

3. По полученным расчётным значениям уровней ряда рассчитываются абсолютные приросты.

4. Рассчитываются гармонические веса по формуле

,

5. Определяются гармонические коэффициенты по формуле

,

6. Определяется средневзвешенное значение прироста.

7. Последующий уровень временного ряда определяется путём прибавления к последующему расчётному значению ряда динамики среднего прироста.

Этот метод может быть использован при выполнении основных предпосылок:

1. Исследуемое экономическое явление должно наблюдаться достаточно продолжительное время, быть инерционным, временной ряд не должен иметь значительных скачкообразных изменений.

2. Отклонения от скользящего тренда должны представлять собой случайный процесс.

Р ассмотрим один из возможных способов временной адаптации с использованием сдвига данных.

Пусть статистическая зависимость имеет вид:

t	1	2	3	4	5	6	7	8	9	10
	5.31	5.42	6.07	6.11	6.53	6.04	7.38	7.46	7.58	7.8

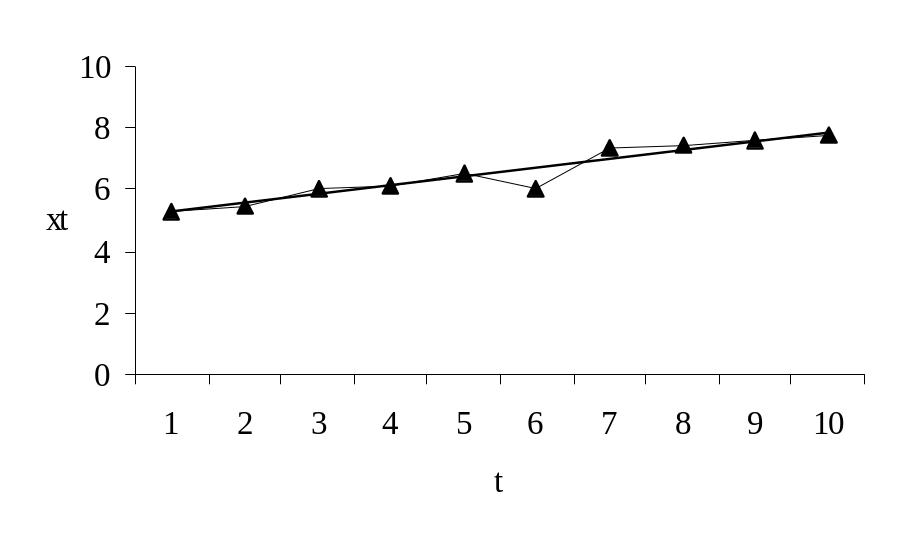
Тренд имеет вид: ; .

Пусть в следующем году , ; тогда тренд с учетом новой информации без значения при :

, .

Пример

Пусть временной ряд характеризуется следующими условиями

t	1	2	3	4	5	6	7	8	9
y	10	11,1	12,1	12,5	13,7	13,9	19,6	15,9	19

1. Проверяется соответствие исходным предпосылкам

2. Определяются параметры трендов. Выбираем , тогда следующие уравнения трендов:

3. С помощью полученных уравнений трендов определяем значения точек скользящего тренда:

а)

б)

откуда

в)

откуда

г)

откуда

и так далее. Следовательно,

t	1	2	3	4	5	6	7	8	9
y	10	11,1	12,1	12,5	13,7	13,9	19,6	15,9	19
	10,02	11,13	12	12,68	13,53	13,99	14,55	16,15	18,74

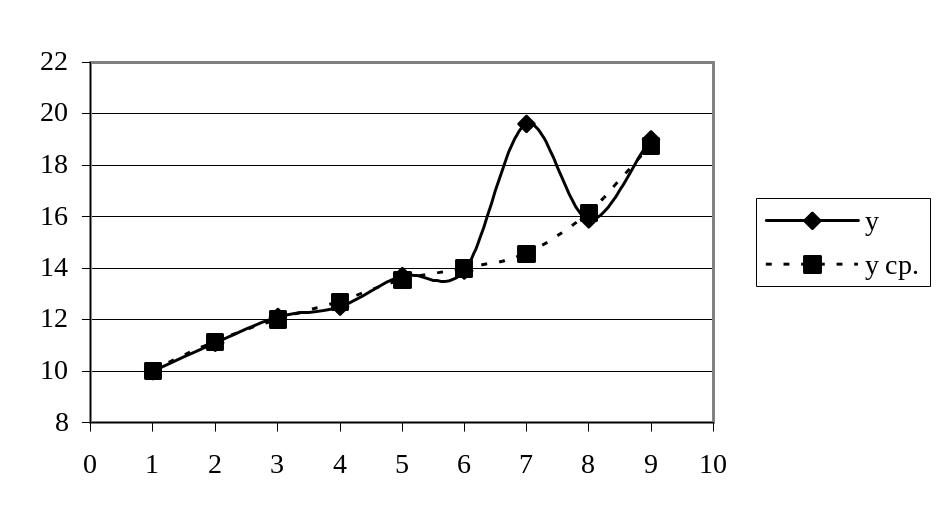
Далее были проверены гипотезы о том, что отклонение от скользящего тренда представляют собой стационарный случайный процесс, что и подтвердилось.

4. Расчёт приростов по формуле

5. Гармонические веса определяются по формуле

следовательно,

6. Гармонические коэффициенты определяются по формуле:

Следовательно,

Проверяются условия:

– выполняется;

– выполняется.

7. Определяется средний абсолютный прирост:

8. Доверительные интервалы прогноза находятся, используя неравенство Чебышева для случайной величины W_t+1.

где a – заданное целое положительное число.

При этом а является функцией отдалённости от L, где L =1,2,3… Функция a (L) определяется по формуле:

И доверительные границы для предсказанных значений будут

Для нашего примера , значение а примем равным 4.

Сделаем прогноз на 5 лет:

t	y			Нижний доверит. интервал	Верхний доверит. интервал
1	10,1	10,02
2	11,1	11,13
3	12,1	12
4	12,5	12,68
5	13,7	13,53
6	13,9	13,99
7	19,6	14,55
8	15,9	16,15
9	19,0	18,74
10			20,25	18,4	22,16
11			21,76	19,32	24,2
12			23,27	20,45	26,09
13			24,78	21,69	27,87
14			26,89	23,01	29,57

Где

и т. д.