4.7. Динамические модели авторегрессии
Модель называется динамической моделью авторегрессии, если результатный признак зависит не только от времени и значений факторных признаков, но и от значений результатного признака в предыдущие моменты (промежутки) времени.
Например:
.
Здесь а1
характеризует краткосрочное изменение
yt под
действием изменения xt
на 1 ед. К моменту t + 1
результат yt
изменится под действием изменения
изучаемого фактора в момент времени t
на a1 ед., а yt+1
под воздействием своего изменения в
непосредственно предшествующий момент
времени – на с1 ед. Таким образом,
общее абсолютное изменение результата
в момент t + 1 составит
ед. Аналогично в момент времени t
+ 2 абсолютное изменение результата
составит
ед. и т. д. Следовательно, долгосрочный
мультипликатор в модели авторегрессии
можно рассчитать как сумму краткосрочного
и промежуточного мультипликаторов:
В модели
авторегрессии вводится условие
стабильности, то есть
.
Поэтому:
.
Пример
По данным о динамике потребления и дохода в регионе получена модель авторегрессии:
.
Таким образом,
краткосрочный мультипликатор равен
0,85– это предельная склонность к
потреблению в краткосрочном периоде.
Следовательно, увеличение среднедушевого
совокупного дохода на 1 тысячу рублей
приводит к росту объема потребления в
тот же год в среднем на 850 рублей.
Долгосрочную склонность к потреблению
можно определить в соответствии с
формулой:
,
то есть в долгосрочной перспективе рост
среднедушевого совокупного дохода на
1 тысячу рублей приведёт к росту объема
потребления в среднем на 944 рубля.
4.8. Выравнивание одномерного временного ряда
Как показано выше, в основе моделирования динамических зависимостей лежит моделирование одномерных динамических рядов, структура которых характеризуется наличием трендов, циклических и случайных колебаний. Поэтому рассмотрим, каким образом происходит выделение трендов и циклических колебаний. Это означает в первую очередь устранение случайной составляющей и в зависимости от цели исследования либо выделение трендовой, либо циклической составляющей.
Основными методами выделения трендов являются: фильтрация, с помощью которой происходит как случайной, так и циклической составляющей, и аналитическое описание, т.е. аппроксимация какой-либо подходящей аналитической зависимости. Для аналитического описания используется МНК. Основными методами выделения циклических составляющих (волн) также являются: фильтрация (для устранения случайных колебаний), устранение глобального тренда и аналитическое описание с помощью МНК путем расположения в ряды Фурье. Фильтрация чаще всего производится путем использования метода скользящих средних. Путем изменения диапазона чисел, для которых определяется средняя величина, изменяется порог фильтрации.
Рассмотрим процесс построения динамической модели на основе рассмотренного выше примера. Предварительный визуальный и автокорреляционный анализ показал наличие в уровнях динамического ряда значительной циклической и трендовой составляющих.
Выравнивание исходного ряда методами скользящей средней:
-
t
Скол. сред. (
)0
0,5
1
2,7
9,7
3,23
2
6,5
13,9
4,63
3
4,7
13,5
4,5
4
2,3
12,2
4,07
5
5,2
16
5,33
6
8,5
20,8
6,93
7
7,1
21,6
7,2
8
6
20,1
6,7
9
7
24,2
8,07
10
11,2
28,2
9,4
11
10
29,4
9,8
12
8,2
27,4
9,13
13
9,2
29,9
9,97
14
12,5
34,9
11,63
15
13,2
36,2
12
16
10,5
При выравнивании по 5 членам получим:
-
t
Скол. сред.
Скол. сред.
0
0,5
1
2,7
2
6,5
16,7
3,34
3
4,7
21,4
4,28
4,34
4
2,3
27,2
5,44
5,29
5
5,2
27,8
5,56
5,76
6
8,5
29,1
5,82
5,83
7
7,1
33,8
6,76
6,76
8
6
39,8
7,96
7,86
9
7
41,3
8,26
8,89
10
11,2
42,4
8,48
8,39
11
10
45,6
9,12
9,16
12
8,2
51,1
10,22
9,19
13
9,2
53,1
10,62
10,69
14
12,5
53,6
10,72
15
13,2
16
10,5
При средней по трем членам имело место проявления цикличности, а при средней по 5 членам цикличность проявляется не так заметно. Сглаживание по 7 членам не дает значительного снижения цикличности. Построим график скользящей средней по 5 членам:
С помощью МНК (с помощью STATGRAPHICS) определим трендовую составляющую (линейную)
.
При этом коэффициент детерминации
,
коэффициент корреляции r
= 0,99.
Таблица ряда при этом примет вид:
-
t
0
0,5
2,37
-1,87
1
2,7
3,01
-0,31
2
6,5
3,65
2,85
3
4,7
4,29
0,41
4
2,3
4,93
-2,63
5
5,2
5,57
-0,37
6
8,5
6,21
2,29
7
7,1
6,85
0,25
8
6
7,49
-1,4
9
7
8,13
-1,13
10
11,2
8,77
2,43
11
10
9,41
0,59
12
8,2
10,05
-1,85
13
9,2
10,69
-1,49
14
12,5
11,33
1,17
15
13,2
11,97
1,23
16
10,5
12,61
-2,11
Д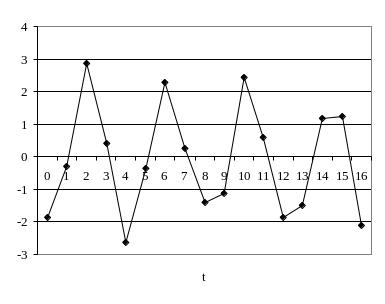
алее
выделим сумму циклической и случайной
составляющей
и
нанесем её на график:
Выделение циклической составляющей производится путем разложения в ряд Фурье
,
т.е.
(суммы берутся от 0 до 15, так как 16 – начало нового цикла).
Увеличим число точек до 12 на одном цикле (цикл = 4) и найдем средние показатели циклической волны.
-
t
0 - 4
-1,87
-1
-0,5
-0,31
0,8
1,8
4 - 8
-2,63
-1,8
-1
-0,37
0,5
1,3
8 – 12
-1,4
-1,8
-1,5
-1,13
0,2
1
12 - 16
-1,85
-2
-1,6
-1,49
-0,5
0,5
-1,94
-1,65
-1,15
-0,825
0,25
1,15
-
t
0 - 4
2,85
2
1,3
0,41
-0,4
-1,5
4 - 8
2,29
1,9
1,2
0,25
-0,3
-0,8
8 – 12
2,43
1,9
1,2
0,59
-0,2
-0,8
12 - 16
1,17
2
1,8
1,23
0,1
-1,5
2,185
1,8
1,4
0,52
-0,2
-1,15
Используем разложение в ряд Фурье:
k – номер гармоники ряда Фурье.
Для отыскания параметров уравнения используется МНК:
, найдя частные производные и приравняв
нулю, получим формулы для вычисления
параметров:
В нашем случае:
Каждому отсчету ti соответствует своя фаза.
-
0
1
2
3
4
5
6
Фаза
0
1
0,866
0,5
0
-0,5
-0,866
-1
0
0,5
0,866
1
0,866
0,5
0
-1,97
-1,65
-1,15
-0,825
0,25
1,15
2,185
-1,94
-1,43
-0,57
0
-0,125
-1
-2.2
0
-0,82
-1
-0,82
0,22
0,57
0
-1,726
-1,81
-1,39
-0,6
0,37
1,25
1,8
-
7
8
9
10
11
12
Фаза
-0,866
-0,5
0
0,5
0,866
1
-0,5
-0,866
-1
-0,866
-0,5
0
1,8
1,4
0,62
-0,2
-1,15
-1,56
-0,69
0
-0,1
-1
-1,94
-0,9
-1,2
-0,62
-0,17
0,57
0
1,88
1,47
0,67
0,29
-1,17
-1,726
(почти 0)
-
-1,726
-1,81
-1,39
-0,6
0,37
1,25
1,8
-
1,88
1,47
0,67
0,29
-1,17
-1,726
Приближение будет более точным при учете 2-ой гармоники.
В целом
имеют вид:
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
0,5 |
2,7 |
6,5 |
4,7 |
2,3 |
5,2 |
8,5 |
7,1 |
6 |
|
2,37 |
3,01 |
3,65 |
4,29 |
4,93 |
5,57 |
6,21 |
6,85 |
7,49 |
|
-1,73 |
-0,6 |
1,8 |
0,67 |
-1,73 |
-0,6 |
1,8 |
0,67 |
-1,73 |
|
0,64 |
2,41 |
5,45 |
4,96 |
3,2 |
4,97 |
8,01 |
7,52 |
5,76 |
|
-0,14 |
0,29 |
1,05 |
-0,26 |
-0,9 |
0,23 |
0,49 |
-0,42 |
0,24 |
t |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
7 |
11,2 |
10 |
8,2 |
9,2 |
12,5 |
13,2 |
|
8,13 |
8,77 |
9,41 |
10,05 |
10,69 |
11,33 |
11,97 |
|
-0,6 |
1,8 |
0,67 |
-1,73 |
-0,6 |
1,8 |
0,67 |
|
7,53 |
10,57 |
10,08 |
8,32 |
10,09 |
13,13 |
12,84 |
|
-0,53 |
0,63 |
-0,08 |
-0,12 |
-0,89 |
-0,63 |
0,36 |
т.е. в пределах 10%
Таким образом, общая модель динамического процесса имеет вид:
Определим ошибки аппроксимации:
-
t
0
1
2
3
4
5
6
7
0,5
2,7
6,5
4,7
2,3
5,2
8,5
7,1
0,64
2,41
5,45
4,96
3,2
4,97
8,01
7,52
-0,14
0,29
1,05
-0,26
-0,9
0,23
0,49
-0,42
-
t
8
9
10
11
12
13
14
15
6
7
11,2
10
8,2
9,2
12,5
13,2
5,76
7,53
10,57
10,08
8,32
10,09
13,13
12,84
0,24
-0,53
0,63
-0,08
-0,12
-0,89
-0,63
0,36
Средняя линейная ошибка аппроксимации:
Практически одинаково.
Таким образом, можно сделать ближайший прогноз значения функции.
(истинное значение 10,5)