10 Клас

1. По заданих координатах однієї точки комп'ютерна програма будує графік за правилом: для кожної точки з координатами генерується й зображується нова точка з координатами . З'ясуйте, чи належить побудованому зображенню точка з координатами (2013, 2014), якщо першою була точка з координатами (2012, 2013)?

Відповідь. Не належить.

Розв'язок. Сума координат кожної точки , що генерується програмою, є величина незмінна (інваріант): . Спочатку для (2012, 2013) сума була , а сума координат точки (2013, 2014) дорівнює , отже, одержати пару (2013, 2014) неможливо.

2. Знайдіть усі натуральні значення n, для яких число є простим.

Відповідь. Таких натуральних значень не існує.

Розв'язок. Розкладемо даний вираз на множники:

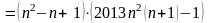. Дане число буде простим тоді й тільки тоді, коли один з отриманих множників рівний 1, а другий множник – просте число. Із того, що при всіх натуральних значеннях n, тоді n² – n+ 1 = 1, тобто, n(n – 1) = 0. Це рівняння в натуральних числах має єдиний розв'язок: n = 1. При цьому значенні n множник дорівнює 4025, ділиться на 5.

3. На сторонах опуклого чотирикутника , як на діаметрах, побудовані кола. Коло, побудоване на стороні , дотикається кола, побудованого на стороні , в точці . У цій же точці дотикаються одне одного кола, що побудовані на сторонах і . Доведіть, що – ромб.

Доведення.

Н ехай і 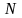- середини сторін , , і відповідно, а, отже, і центри відповідних кіл. Оскільки кола, що побудовані на сторонах і , мають спільну дотичну, то точки , і лежать на одній прямій. Аналогічно, точки , і лежать на одній прямій. З іншого боку, - паралелограм, тому й , тобто - паралелограм.

Точка - точка перетину діагоналей паралелограма . Кути АОВ, ВОС, COD, DOA по 90^о, як вписані, що спираються на діаметри. А тому ці діагоналі перпендикулярні. Таким чином - ромб, що й було потрібно довести

4. Розв'яжіть рівняння .

Відповідь: розв'язків немає

Розв'язок Перепишемо ліву частину рівняння у вигляді

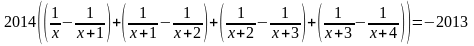
Тоді після приведення подібних отримаємо , де 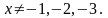Позбувшись від знаменника, одержимо квадратне рівняння , дискримінант якого від’ємний .

5. Таблиця 5 5 заповнена числами 1, 2, ..., 25, причому будь-які два послідовних числа записані в сусідні (що мають спільну сторону) клітинки. Яка найбільша кількість простих чисел може бути в одному рядку?

Розв'язок

Розфарбуємо клітки даної таблиці в шаховому порядку. Довести, що в клітках одного кольору будуть стояти непарні числа, а в клітках іншого кольору – парні. У будь-яких двох сусідніх клітках розташовані числа різної парності (13 непарних та 12 парних).

Таким чином, у будь-якому стовпці повинно бути не менш двох парних чисел, тому простих непарних чисел у стовпці може бути не більше трьох, але в одному із стовпців є 2 – просте число, а тому у стовпці може бути і чотири простих, серед яких обов'язково повинне бути число 2.

Одне з можливих розміщень, що задовольняють умові задачі, наведено на малюнку (чотири прості числа – у третьому стовпці).

13	14	15	16	25
12	9	8	17	24
11	10	7	18	23
2	1	6	19	22
3	4	5	20	21

ПРОТОКОЛ

заседания жюри городской олимпиады по дисциплине «Физика» среди студентов Образовательных учреждений среднего профессионального образования Ростова на Дону

От « 21» апреля 2009 г.

Председатель жюри: Лебединская Алла Робертовна-председатель УМО по физике, кандидат физико-математических наук, доцент, преподаватель физики ГОУ СПО "Ростовский-на-Дону государственный колледж связи и информатики"

Члены жюри:

1. Кашуба Михаил Павлович - преподаватель физики ГОУ СПО "Ростовский электротехнический колледж"

2. Иващенко Ольга Николаевна - преподаватель физики ГОУ СПО «Ростовский финансово-экономический колледж», филиал фин. Академии

3. Харитонов Евгений Григорьевич - преподаватель физики ГОУ СПО "Ростовский-на-Дону государственный колледж радиоэлектроники информационных и промышленных технологий»

ПОВЕСТКА:

1. Подведение итогов и определение победителей городской олимпиады по дисциплине «Физика» среди студентов образовательных учреждений среднего профессионального образования г. Ростова-на-Дону

2. СЛУШАЛИ: об итогах выполнения конкурсных заданий областной олимпиады по дисциплине «Физика» студентами образовательных учреждений г. Ростова-на-Дону

ПОСТАНОВИЛИ:

1. Признать победителями городской областной олимпиады по дисциплине «Физика» ниже поименованных студентов:

Место	Наименование учебного заведения	ФИО участника	ФИО преподавателя
1 место	ГОУ СПО "Ростовский-на-Дону электротехнический колледж"	Горянский Евгений Борисович	Кашуба Михаил Павлович
2 место	ГОУ СПО «Ростовский-на-Дону государственный колледж связи и информатики»	Гаврилова Алла Викторовна	Лебединская Алла Робертовна
2 место	ГОУ СПО "Ростовский-на-Дону электротехнический колледж"	Радько Вячеслав Андреевич	Кашуба Михаил Павлович
3 место	ГОУ СПО "Ростовский-на-Дону электротехнический колледж"	Севрюков Виктор Алексеевич	Кашуба Михаил Павлович
3 место	ГОУ СПО «Ростовский-на-Дону государственный колледж связи и информатики»	Гаврилко Дмитрий Валерьевич	Дронова Раиса Васильевна

2. Студентов, занявших 1-е, 2-е и 3-е места дипломами, согласно положению о проведении городской олимпиады.

3. Ходатайствовать перед Советом директоров ССУЗов г. Ростова на Дону о награждении преподавателей образовательных учреждений среднего профессионального образования, подготовивших победителей и призеров городской олимпиады, почетными грамотами.

4. В городской олимпиаде приняло участие 19 участников из 7 колледжей г. Ростова-на-Дону.

5. Ходатайствовать перед Советом директоров ССУЗов Ростова на Дону об объявлении благодарности за организацию и проведение олимпиады администрации Ростовского на Дону государственного колледжа связи и информатики: начальнику отдела НИР Михайлиной Светлане Кимовне, начальнику отдела информатизации Ковалищенко Игорю Игоревичу.

Голосовали: единогласно

Председатель жюри:		А.Р.Лебединская
Члены жюри:		М.П.Кашуба
		О.Н. Иващенко
		Е.Г.Харитонов