Завдання для підготовки до олімпіади з математики серед студентів І курсів
Розділ 1
Тотожні перетворення алгебраїчних виразів. Алгебраїчні рівняння, системи рівнянь та нерівності. Побудова графіків функцій.
1. Розв’яжіть рівняння:
1.1.
;
1.2.
.
1.3.
1.4.
1.5.
1.6.
1.7.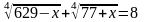
1.8.
;
1.9.
1.10.
1.11.
1.12.
1.13.
1.14.
1.15.
1.16.
1.17.
1.18.
1.19.
1.20.
1.21.
Знайти суму коренів рівняння:
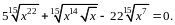
1.22.
Знайти суму коренів рівняння:
1.23.
Знайти суму коренів рівняння:
1.24.Знайти
суму коренів рівняння:
1.25.
Знайти суму коренів рівняння:
1.26.
;
1.27. 2(х2+х+1)2-7(х2–2х+1)–13(х3–1)=0;
1.28. (х + 1) (х + 3)(х + 5)(х + 7) + 15 = 0;
1.29. (х + 2) (х – 4)(х – 7)(х – 1) = 40;
1.30.
;
1.31.
;
1.32.
;
1.33.
;
1.34.
;
1.35.
;
1.36.
;
1.37.
;
1.38.
1.39.
;
1.40. ;
1.41. (х2 – 2х + 2)2 + 3х(х2 – 2х + 2) = 10х2;
1.42. (х2 + х + 4)2 + 8х(х2 + х + 4) + 15х2 = 0;
1.43. (х – 3) (х + 4)(х + 6)(х – 2) = 10х2;
1.44.
;
1.45.
;
1.46. (х – 2)4 + (х – 3)4 = 1;
1.47. (х – 6)4 + (х – 4)4 = 82;
1.48. (5 – х)4 + (2 – х)4 = 17;
1.49. (2х – 3)4 + (2х – 5)4 = 2;
1.50.
1.51.
1.52.
1.53.
2. Спростіть вирази:
2.1.
Спростіть вираз і обчисліть, якщо
:
Спростіть вираз:
Спростити вираз:
Спростити вираз:
Спростіть вираз:
Спростити вираз:
2.7.
Обчисліть значення виразу:
2.8.
Обчисліть значення виразу:
2.9.
Обчисліть значення виразу:
2.10.
Обчисліть значення виразу:
2.11.
Обчисліть значення виразу:
2.12.
Спростіть вираз:
2.13.
Спростіть вираз:
2.14.
Спростіть вираз:
2.15.
Спростіть вираз:
2.16.
Спростіть вираз:
,
при
.
2.17.
Спростіть вираз:
,
при
.
2.18.
Спростіть вираз:
,
при
2.19.
3. Розв’яжіть системи рівнянь:
3.1
;
3.2.
;
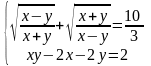3.3.
;
3.4.
;
3.5.
;
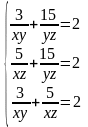3.6.
;
3.7.
3.8.
3.9.
4. Розв’яжіть нерівність:
4.1.
4.2.
4.3.
4.4.
4.5.
.
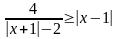4.6.
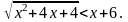
4.7.
4.8.
4.9.
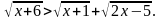
4.10.
4.11.
5. Побудувати графіки функцій:
5.1.
5.2.
5.3.
5.4.
5.5.
5.6.
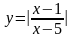
5.7.
Розділ 2 Тригонометричні функції, рівняння.
1. Спростіть вирази:
1.1.
Спростіть вираз
і обчисліть його значення при
.
1.2.
Спростіть вираз
і обчисліть його значення при
.
1.3.
Знаючи, що
і
,
знайти
.
1.4.
Знаючи, що
,
знайти
1.5.
Обчислити:
,
якщо
;
1.6.
,
якщо
;
1.7.
,
якщо
.
2. Розв’яжіть рівняння:
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
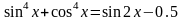
2.8.
2.9.
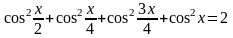
2.10.
2.11.
2.12.
2.13.
2.14.
2.15.
2.16.
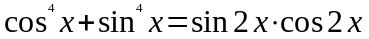
2.17.
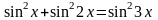
2.18.
2.19.
2.20.
2.21.
2.22.
2.23.
2.24.
2.25.
2.26.
2.27.
2.28.
2.29.
2.30.
3. Побудуйте графіки функцій:
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
y = 2 |cos (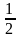
x
– π/4)| – 1
3.9.
3.10.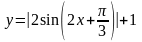
.
3.11.
3.12.
3.13.
3.14.
3.15.
3.16.
Розділ 3 Показникові та логарифмічні функції, рівняння, нерівності та їх системи.
1. Показникові та логарифмічна функції. Логарифм числа.
1.1
Знайдіть найменше ціле число, що входить
в область визначення функції
.
1.2.За
яких значень
визначена функція
?
1.3.Знайдіть
найбільше ціле число, що входить в
область визначення функції
.
1.4.
Знайдіть область визначення функції
.
1.5.
Знайдіть область визначення функції
.
1.6.
Обчисліть:
1.7.
Дано
.
Знайдіть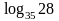
1.8.
Обчисліть:
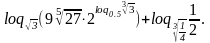
1.9.
Обчисліть:
.
1.10.
Обчисліть:
.
1.11.
Обчисліть: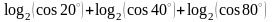
.
1.12.
Обчисліть:
2. Розв’яжіть рівняння:
2.1.
2.2.
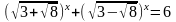
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
2.11.
.
2.12.
2.13.
.
2.14.
.
2.15.
;
2.16.
;
2.17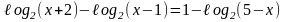
2.18.
2.19.
2.20.
2.21.
2.22.
2.23. logx (2x2 - 4x + 3) = 2
2.24. lq x² = 0,25 lq (4x + 3x)4
2.25.
2.26.
2.27.
2.28.
2.29.
2.30
2.31.
2.32.
2.33.
2.34.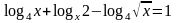
2.35
2.36.
2.37.
2.38.
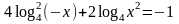
2.39.
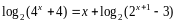
2.40.
.
2.41.
.
2.42.
2.43.
.
2.44.
.
2.45.
3. Розв’яжіть нерівності:
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
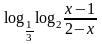
3.7.
3.8.
3.9.
3.10.
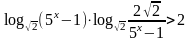
3.11.
3.12.
3.13.
3.14.
3.15.
3.16.
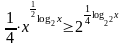
3.17.
3.18.
3.19.
3.20.
3.21.
3.22.
3.23.
.
3.24.
.
3.25.
.
4. Розв’яжіть системи рівнянь:
4.1.
4.2.
4.3.
4.4.
4.5.
4.6.
4.7.
4.8.
4.9.
4.10.
4.11.
4.12.
4.13.
4.14.
4.15.
Знайти значення виразу
,
де
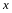та
задовольняють систему рівнянь:
4.16.
4.17.
4.18.
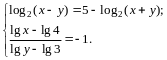
4.19.
4.20.
4.21.
4.22.
Розділ 4 Похідна та її застосування
Знайдіть похідну функції:
1.1
1.2.
1.3.
1.4.
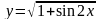
1.5.
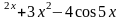
1.6.
1.7.
1.8.
1.9.
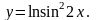
1.10.
1.11.
1.12.
1.13.
1.14.
1.15.
1.16.
1.17.
1.18.
1.19.
1.20.
1.21.
1.22.
1.23
1.24.
1.25.
1.26.
1.27.
1.28.
1.29.
1.30.
1.31.
1.32.
2. Застосування похідної.
2.1.
Знайти проміжки зростання і спадання
та точки екстремумів функції
.
2.2.
Знайти проміжки зростання і спадання
та точки екстремумів функції
2.3.
Знайти проміжки зростання і спадання
та точки екстремумів функції
2.4.
Знайти проміжки зростання і спадання
та точки екстремумів функції
2.5.
Знайти проміжки зростання і спадання
та точки екстремумів функції
.
2.6.
Знайти проміжки зростання і спадання
та точки екстремумів функції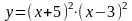
2.7.
Знайти проміжки зростання і спадання
та точки екстремумів функції
2.8.
Дослідити
на екстремум функцію
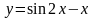в
інтервалі
.
2.9.
Знайти
критичні точки функції
2.10. Знайти найменше та найбільше значення функції на заданому проміжку:
.
2.11. Знайти найменше та найбільше значення функції на заданому проміжку:
;
2.12. Знайти найменше та найбільше значення функції на заданому проміжку:
,
.
2.13.
Знайдіть найменше значення функції
на
проміжку
.
2.14. Знайти найменше та найбільше значення функції на заданому проміжку:
,
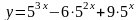якщо х
є [–1;1];
2.15. Знайти найменше та найбільше значення функції на заданому проміжку:
,
якщо х
є [–1;3];
2.16. Знайти найменше та найбільше значення функції на заданому проміжку:
,
якщо х
є [9;243];
2.17. Знайти найменше та найбільше значення функції на заданому проміжку:
,
якщо х
є [
;32].
2.18.
Скласти
рівняння дотичної до графіка функції
у точці з абсцисою
.
2.19.
До
кривої
з точки М(3;10) проведені дві дотичні.
Знайти кут між ними, та площу трикутника,
утвореного цими дотичними та віссю
Ох.
2.20.
В
точці
до
кривої
проведена дотична.
Знайти
довжину її
відрізка,
вміщеного
між
осями
координат.
2.21.
До
графіка
функції
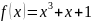в
точці з абсцисою
проведена
дотична. Знайти абсцису точки графіка
дотичної, ордината якої 31.
2.22.
Залежність шляху від часу при прямолінійному
русі точки задана рівнянням
.
Знайти швидкість точки через 2секунди
після початку руху.
2.23.
Дано функцію
.
Знайдіть значення сталих
і
,
якщо
.
2.24.
Дано функцію
.
Знайдіть область значень похідної
.
2.25.Знайдіть
число розв’язків рівняння
на відрізку
,
де
.
2.26.
Знайдіть корені рівняння
,
якщо
.
2.27. Знайти найменшу довжину (l) огорожі, за допомогою якої можна обгородити ділянку в формі прямокутника з даною площею (S), який прилеглий до стіни.
2.28. В прямокутний трикутник з гіпотенузою 8см і кутом 60° вписаний прямокутник, основа якого лежить на гіпотенузі. Якими повинні бути розміри прямокутника, щоб його площа була найбільшою?
2.29. Серед всіх рівнобічних трикутників з бічною стороною знайдіть трикутник найбільшої площі.
2.30. Знайти число, куб якого перевищує потрійний його квадрат на мінімальне значення.
2.31. Знайти додатне число, сума якого зі своєю оберненою величиною мала би найменше значення.