Лабораторная работа №1

Построение математической модели процесса гальванического получения хромоникелевых покрытий.

Цель работы. Ознакомление с методом планирования эксперимента и построения математической модели гальванического процесса.

Введение. Для получения плотных хромоникелевых покрытий с минимальными внутренними напряжениями применяется электрохимическое выделение из сернокислых растворов. Внутренние напряжения могут быть измерены по деформации металла. Представляет интерес изучение влияния параметров электрохимического процесса на качество гальванического покрытия.

Содержание работы. Важнейшим условием научно поставленного эксперимента является минимизация общего количества опытов, а следовательно, и затрат материальных, трудовых и временных ресурсов, что конечно не должно существенно отражаться на качестве полученной информации.

При создании математической модели процесса с использованием метода планирования эксперимента следует выделить следующие основные этапы:

1. Выбор входных и выходных данных.

Входные переменные Х_i, i= , которые определяют состояние объекта, называются влияющими факторами. Основное требование к ним – достаточная управляемость, т.е. возможность установить нужный уровень фактора и стабилизировать его в течение опыта. Выходная переменная Y (функция отклика) – реакция объекта на входные воздействия. Выбор определяется целью исследования, которая может представлять оптимизацию экономической, технологической или иной другой характеристики объекта.

2. Выбор области экспериментирования.

Подразумевается выбор области факторного пространства, изучение которой представляет интерес для исследования. Границы области по каждому фактору Х_i обусловлены его минимальными и максимальными значениями, т.е. Х_{i min} < Х_i < Х_{i max}. При выборе ограничений исследователь руководствуется конкретными обстоятельствами, например: временем протекания процесса, стоимостью материала и др.

3. Выбор математической модели объекта.

В случае, если аналитическая зависимость, связывающую функцию отклика с влияющими факторами, найти невозможно и вид функции Y = (Х_1, Х_2,…. Х_k) априори неизвестен, то целесообразно использовать степенной ряд:

Y = a₀ 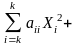…., (I)

где k- число влияющих факторов.

Выражение (I) служит математической моделью исследуемого объекта. Для определения коэффициентов аппроксимирующего полинома применяется наиболее универсальный метод наименьших квадратов. При его использовании необходимым условием получения статистических оценок является выполнение неравенства N>s, т.е. количество опытов N должно быть больше чем число коэффициентов полинома s.

Для удобства обработки и интерпретации результатов эксперимента целесообразно все факторы представить в безразмерной форме, для чего проводят операцию кодирования переменных:

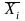=0,5 (Х_{i min} + Х_{i max}.); I = 0,5 (Х_{i min} - Х_{i max}.); x_{i min} = 1,0; x_{i max} = +1,0

Для количественных факторов связь между физическими Х_i и кодированными x_i значениями факторов определяется соотношением x_i = (Х_i - ) / I_i.

Описанные преобразования являются линейными, поэтому в аппроксимирующей функции (I) изменяются только коэффициенты при факторах, т.е.:

Y = b₀ …., (II)

При практической аппроксимации обычно ограничиваются учетом линейного и квадратичного влияния факторов, а также эффектов их парного взаимодействия.