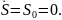МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИ

ФГБОУ ВПО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра теоретической механики

КУРСОВАЯ РАБОТА

ПО РАЗДЕЛУ "ДИНАМИКА"

«ИССЛЕДОВАНИЕ КОЛЕБАНИЙ МЕХАНИЧЕСКОЙ

СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ»

Вариант № 1

Выполнил: студент гр. 121231с Ополовнин Н. С., шифр 140400

Научный руководитель: доцент

Тула, 2013

ОГЛАВЛЕНИЕ

АННОТАЦИЯ 3c

СХЕМА МЕХАНИЗМА И ДАННЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ 4c

1. ВЫВОД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ДВИЖЕНИЯ С ИСПОЛЬЗОВАНИЕМ ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ 5c

2. ОПРЕДЕЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ СИСТЕМЫ 10c

3. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ВНЕШНИХ И ВНУТРЕННИХ СВЯЗЕЙ 12c

4. СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЗМА С ПОМОЩЬЮ ПРИНЦИПА ДАЛАМБЕРА-ЛАГРАНЖА 15c

5. СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЗМА С ПОМОЩЬЮ УРАВНЕНИЯ ЛАГРАНЖА 2-ГО РОДА. 19c

6. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ 21c

7. АНАЛИЗ РЕЗУЛЬТАТОВ 27c

СПИСОК ЛИТЕРАТУРЫ 28c

Аннотация

В данной курсовой работе исследуется механическая система с одной степенью свободы, представляющая совокупность абсолютно твёрдых тел, связанных друг с другом посредствам невесомых нерастяжимых нитей, параллельных соответствующим плоскостям. Система снабжена внешней упругой связью с коэффициентом жёсткости с. На груз действует возмущающая гармоническая сила F(t)=F0•sin(pt). Система снабжена демпфирующим устройством, в котором возникает сопротивление движению моделируемое парой сил 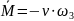. Трением качения и скольжения пренебрегаем. Качение канатов происходит без скольжения, проскальзывание нитей на блоках отсутствует. Блок 2 считается невесомым. Примененяя основные теоремы динамики системы и аналитические методы теоретической механики, определен закон движения первого тела и реакции внешних и внутренних связей.

СХЕМА МЕХАНИЗМА И ДАННЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ

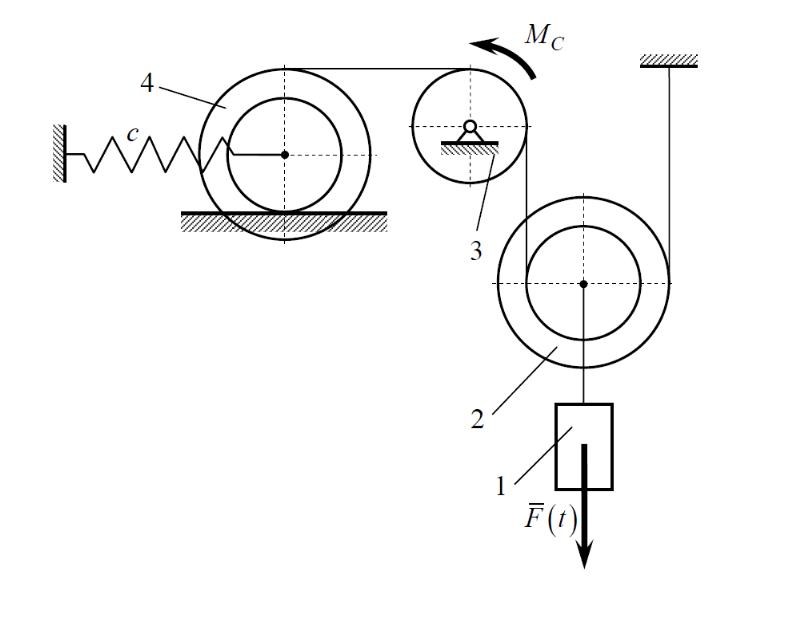
Дано:

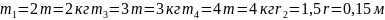
Рис. 1. Схема механизма и исходные данные

1. Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы

Расчётная схема представлена на рисунке 2, здесь обозначено:

Рис. 2.

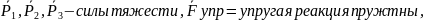
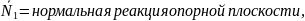
Рассматриваемая механическая система имеет одну степень свободы. Будем определять ее поло­жение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 1

Для построения дифференциального уравнения движения системы используем теорему об изме­нении кинетической энергии механической системы в форме:

(1.1)

где Т - кинетическая энергия системы,

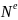- сумма мощностей внешних сил,

- сумма мощностей внутренних сил,

Вычислим, кинетическую энергию системы как сумму кинетических энергий тел, образующие механическую систему:

Груз 1 совершает поступательное движение, его кинетическая энергия: .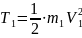

По условию задачи блок 2 считается невесомым, поэтому его кинетическая энергия T₂ = 0.

Блок 3 совершает вращательное движение, его кинетическая энергия: .

где 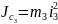– момент инерции относительно центральной оси блока,

– угловая скорость блока.

Каток 4 совершает плоскопараллельное движение, его кинетическая энергия:

,

где V_c4 – скорость центра масс катка;

– момент инерции относительно центральной оси катка;

– угловая скорость катка.

Кинетическая энергия всего механизма равна:

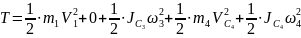(1.2)

Выразим через скорость груза 1:

,

,

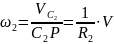; , (1.3)

;

; ,

.

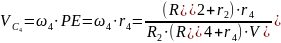Подставляя кинематические соотношения (1.3) в выражение (1.2), получаем:

или , (1.4)

где m_пр – приведенная масса:

,

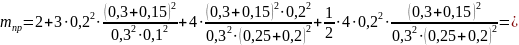
Найдем производную от кинетической энергии по времени: .

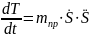Вычислим сумму мощностей внешних и внутренних сил. Мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения:

Мощность, момента силы равна алгебраическому произведению момента силы на угловую скорость вращения тела, к которому приложен момент:

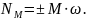
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, не деформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:

Будут равняться нулю мощности следующих внешних сил, приложенных в точках, скорости которых равны нулю: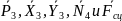 . - Сумма мощностей остальных внешних сил:

,

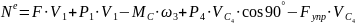
С учетом кинематических соотношений (1.3) сумму мощностей внешних сил определим:

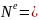
или ,

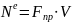где – приведенная сила.

Упругую силу считаем пропорциональной удлинению пружины, которое равно сумме статического λ_ст и динамического 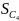удлинений:

Так как

(1.5)

В состоянии покоя системы приведенная сила равна нулю. Полагая в (1.5) и 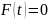, получаем условие равновесия системы:

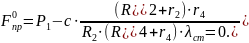
Отсюда статическое удлинение пружины равно:

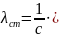
Подставляя выражение (1.6) в (1.5), получаем окончательное выражение для приведенной силы:

Подставив выражения для производной от кинетической энергии и сумму мощностей всех сил с учетом (1.7) в уравнение (1.1), получаем дифференциальное уравнение движения системы:

или

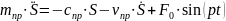
где 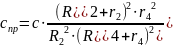– приведенная жесткость пружины.

– приведенный коэффициент сопротивления.

Перепишем предыдущее уравнение в виде:

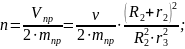
Где - показатель степени затухания колебаний,

– частота свободных колебаний.

Начальные условия движения при t = 0: S = S₀= 0,05м и