Билет № 9
1. Точка движется по окружности радиусом R = 2 м согласно уравнению L = At3, где A = 2 м/с3. В какой момент времени t нормальное ускорение an точки будет равно тангенциальному a? Определить полное ускорение a в этот момент. (L – координата, отсчитываемая по дуге окружности).
2. На горизонтальной плоскости находятся два тела: брусок и электромотор с батарейкой на подставке. Расстояние между обоими телами равно l, коэффициент трения между телами и плоскостью k. После включения мотора брусок, масса которого вдвое больше массы другого тела, начал двигаться с постоянным ускорением a. Через сколько времени оба тела столкнуться?
3. Винтовку навели на вертикальную черту мишени, находящейся точно в северном направлении, и выстрелили. Пренебрегая сопротивлением воздуха найти на сколько сантиметров и в какую сторону пуля, попав в мишень, отклонится от черты. Выстрел произведен в горизонтальном направлении на широте = 60, скорость пули V = 900 м/с, расстояние до мишени S = 1,0 км.
---------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------
Билет № 10
1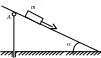
.
Движение точки по кривой задано
уравнениями X = A1t3
и Y = A2t,
где A1 = 1 м/с3,
A2 = 2 м/с.
Найти уравнение траектории точки, ее
скорость V и полное
ускорение a в момент
времени t = 0,8 с.
2. Небольшое тело m начинает скользить по наклонной плоскости из точки, расположенной над вертикальным упором A. Коэффициент трения между телом и наклонной плоскостью k = 0,14. При каком значении угла время соскальзывания будет
наименьшим?
3. Человек массы m = 60 кг идет равномерно по периферии горизонтальной круглой платформы радиуса R = 3,0м, которую вращают с угловой скоростью ω = 1,00 рад/с вокруг вертикальной оси, проходящей через ее центр. Найти горизонтальную составляющую силы, действующей на человека со стороны платформы, если результирующая сил инерции, приложенных к нему в системе отсчета «платформа», равна нулю.
---------------------------------------------------------------------------------------------------------------------
Билет № 11
1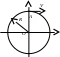
.
Точка А движется равномерно со
скоростью по окружности радиусом
R. Начальное положение
точки и направление движения указаны
на рисунке. Написать кинематическое
уравнение движения проекции точки А
на направление оси X.
2. Шайбу положили на наклонную плоскость и сообщили направленную вверх начальную скорость V0. Коэффициент трения между шайбой и плоскостью равен k. При каком значении угла наклона шайба пройдет вверх по плоскости наименьшее расстояние? Чему оно равно?
3. Поезд массы m = 2000 т движется на северной широте = 60. Определить: а) модуль и направление силы бокового давления поезда на рельсы, если он движется вдоль меридиана со скоростью V = 54 км/ч; б) в каком направлении и с какой скоростью должен был бы двигаться поезд, чтобы результирующая сил инерции, действующих на поезд в системе отсчета «Земля», была равна нулю.