2. Показатели надежности невосстанавливаемых элементов.

К числу широко применяемых количественных характеристик надежности невосстанавливаемых объектов относятся: вероятность безотказной работы P (t); вероятность отказа Q (t); частота отказов a (t); интенсивность отказов λ(t); средняя наработка до первого отказа Tср. Вероятность безотказной работы P (t) – это вероятность того, что при определенных условиях эксплуатации в заданном интервале времени не произойдет ни одного отказа. Вероятность безотказной работы по статистическим данным об отказах оценивается выражением: где P*(t) – статистическая оценка вероятности безотказной работы; N0 – количество изделий в начале испытаний; n (t) – число отказавших объектов за время t. Вероятность отказа Q (t) – это вероятность того, что при определенных условиях эксплуатации в заданном интервале времени произойдет хотя бы один отказ. Вероятность отказа при работе по статистическим данным об отказах оценивается выражением: Вероятность отказа Q (t) является возрастающей функцией времени . Функция Q (t) характеризует вероятность того, что в заданном интервале времени произойдет хотя бы один отказ: Q (t) = Q (tр < t) — вероятность того, что время безотказной работы меньше t. Частота отказов a (t) — плотность распределения времени безотказной работы или производная от вероятности безотказной работы: a (t) = q'(t) = — p'(t).  Для определения величины a (t) используется следующая статистическая оценка: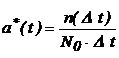 где n (∆t) – количество отказавших изделий в интервале времени ∆t; N0 – количество изделий в начале испытаний. интенсивность отказов λ(t) – это условная плотность распределения времени безотказной работы для момента времени t при условии, что до этого момент отказа не произошел (интенсивность появления отказов в единицу времени причем P (t) ≤ 1, то λ(t) ≥а(t). Для высоконадёжных систем если P (t) = 0.99,то а(t) ≈ λ(t). Ошибка не более 1% и не превышает ошибок статистического определения а(t) и λ(t). Средней наработкой до отказа Tср - это называется математическое ожидание наработки объекта до первого отказа, которое вычисляется следующим образом:  Таким образом, средняя наработка до отказа графически представляет собой площадь, лежащую под графиком функции P (t).

3. Законы распределения, используемые в теории надежности. Оценка основных показателей надежности в период нормальной эксплуатации.

Биноминальный закон распределения числа n – появления события А в m – независимых опытах (испытаниях). Если вероятность появления события А в одном испытании есть р, тогда вероятность не появления события q = 1 – p.

Если независимое число испытаний = m, тогда вероятность появления n событий будет равна: - уравнение Бернулли.

Закон Пуассона.

вероятность возникновения случайного события n раз за время t.

Экспоненциальный закон.

где P(x) это вероятность того что случайная величина X имеет значение большее x.

g распределение.

Е сли отказ устройства возникает тогда когда произойдет не менее k отказов его элементов, а отказы элементов подчинены экспоненциальному закону с параметром l0. Плотность вероятности отказа устройства:

Распределение Вейбула.

Плотность вероятности:

Нормальное распределение (НР).

Случайная величина X возникает тогда когда x зависит от большого числа однородных по своему влиянию случайных факторов, причем влияние каждого из факторов по сравнению с влиянием совокупности остальных незначительно.

Плотность вероятности отказа НР:

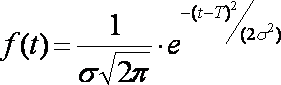
c² – распределение.

Если случайная величина t распределена по НЗ с Т = 0 и = 1, то параметр X = будет являться случайной величиной с плотностью распределения:

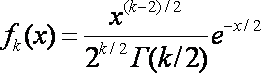
После периода приработки начинается период нормальной эксплуатации, когда интенсивность отказов падает λ(t) и в течение длительного времени остается примерно постоянной. В этот период происходят внезапные отказы, которые носят случайный характер, например из-за случайного повышения нагрузок. Распределение наработки до отказа описывается показательным законом. При этом функция плотности распределения

f(t) = Xexp(-Xt). Вероятность безотказной работы P(t) = exp{-Xt).

При постоянной интенсивности отказов средняя наработка на отказ равна Т = 1/Х.