
- •Елементи матлогіки
- •Алгебра висловлень.
- •Список законів алгебри логіки.
- •Істинні і фіктивні змінні
- •Додавання по модулю 2
- •Штрих Шеффера
- •Суперпозиція і формули
- •Алгебра предикатів
- •Істинні формули і еквівалентні відношення.
- •Наведемо приклад еквівалентних співвідношень
- •Аналогічно доводиться співвідношення
Елементи матлогіки
Алгебра висловлювань
1.Поняття висловлювань
Під висловленням розуміють будь-яке твердження про яке можна сказати, що воно істинне чи хибне.
Наприклад, твердження, що 3>2 істинне, 2>3 – хибне.
Відмітимо, що довільне визначення не являється висловленням. Теореми (будь-яка) є висловленням. Наприклад, колом є замкнута крива, точки якої рівновіддалені від заданої – не є висловленням.
Висловленням є: якщо f(x) диференційована в околі Х0, то вона неперервна.
В подальшому матлогіка не цікавиться змістом висловлень, а лише їх істинністю чи хибністю. Висловлення позначається p, q, r, s, t… Істинне висловлення приймають «1», якщо хибне «0».
Над висловленням визначені наступні операції: заперечення, диз’юнкція, кон’юнкція, імплікація, еквівалентність.
Визначення
Запереченням (
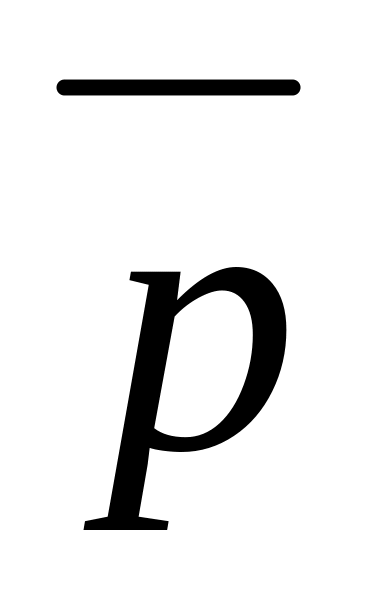 або p)
висловлювання p
є висловлювання, яке істинне, коли
p
– хибне
і хибне, якщо p
істинне.
або p)
висловлювання p
є висловлювання, яке істинне, коли
p
– хибне
і хибне, якщо p
істинне.Диз’юнкцією (
 )
висловлювань p
і
q
називають
висловлення, яке є хибним, коли p
і
q
хибні
і істинне в інших випадках.
)
висловлювань p
і
q
називають
висловлення, яке є хибним, коли p
і
q
хибні
і істинне в інших випадках.Кон’юнкція (
 )
висловлювань p
і
q
називають висловленням, коли воно є
істинне лише коли при p
і
q
– істинні, і хибне в інших випадках.
)
висловлювань p
і
q
називають висловленням, коли воно є
істинне лише коли при p
і
q
– істинні, і хибне в інших випадках.
Імплікація
 висловлень p
і
q
називають висловлення, яке є хибним
лише коли p
істинне
а q
- хибне і істинне в інших випадках.
висловлень p
і
q
називають висловлення, яке є хибним
лише коли p
істинне
а q
- хибне і істинне в інших випадках.Еквівалентністю
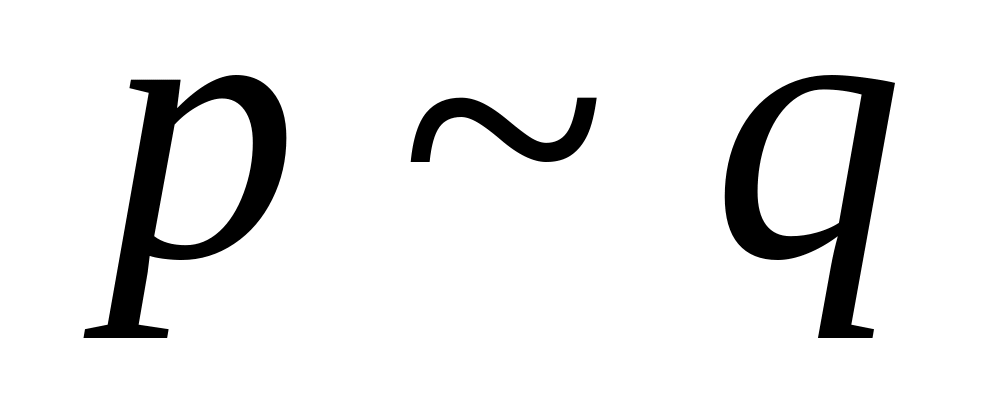 висловлювань p
і
q
називають
висловлення, яке є істинним тоді і
тільки тоді, коли p
і
q
мають
однакові істинності значення.
висловлювань p
і
q
називають
висловлення, яке є істинним тоді і
тільки тоді, коли p
і
q
мають
однакові істинності значення.
Таблиця істинності
змінні |
змінні |
НЕ |
АБО |
І |
ЯКЩО |
Тоді і тільки тоді |
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
Заперечення |
Диз‘юнкція |
Кон‘юнкція |
Імплікація |
Еквівалентність |
|
Через
P
позначено
множену усіх висловлень. На множені P
визначенні:
унітарна операція
і
бінарні
![]() відносно
яких P
є
замкнута ( у множені P
містяться
окрім окремих висловлень також результати
операцій над ними). Оскільки аргументи
функції та результати дії операцій
належать одній і тій ж множині, то виникає
алгебра логіки.
відносно
яких P
є
замкнута ( у множені P
містяться
окрім окремих висловлень також результати
операцій над ними). Оскільки аргументи
функції та результати дії операцій
належать одній і тій ж множині, то виникає
алгебра логіки.
Алгебра висловлень.
Застосовуючи
унітарні та бінарні дії над елементарними
висловленнями можна отримати складне
висловлення
![]() ;
або
;
або
![]() .
.
Запис типу ; або називається формулою алгебри висловлень. Формули позначають великими буквами F, U, V, Y і т.д.
До формул застосовуються означення.
Довільні елементарні висловлення є формулами.
Якщо U, V – формули, то
 ,
,
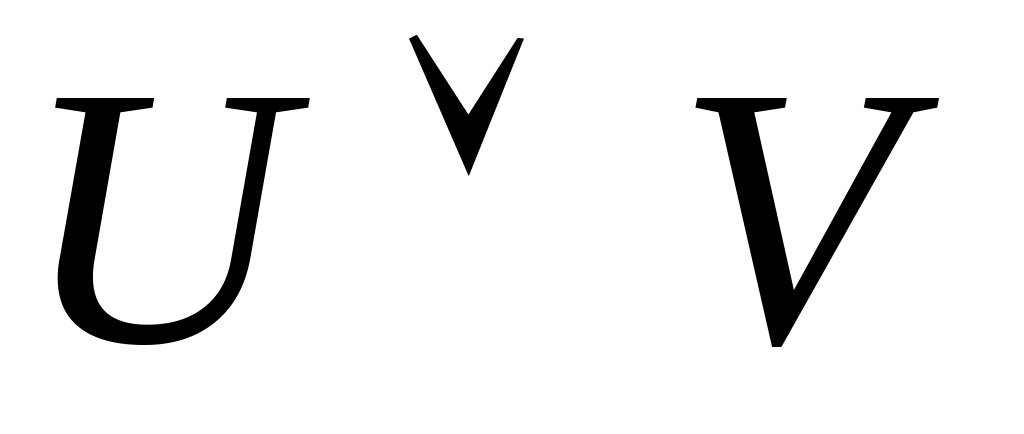 ,
,
 ,
,
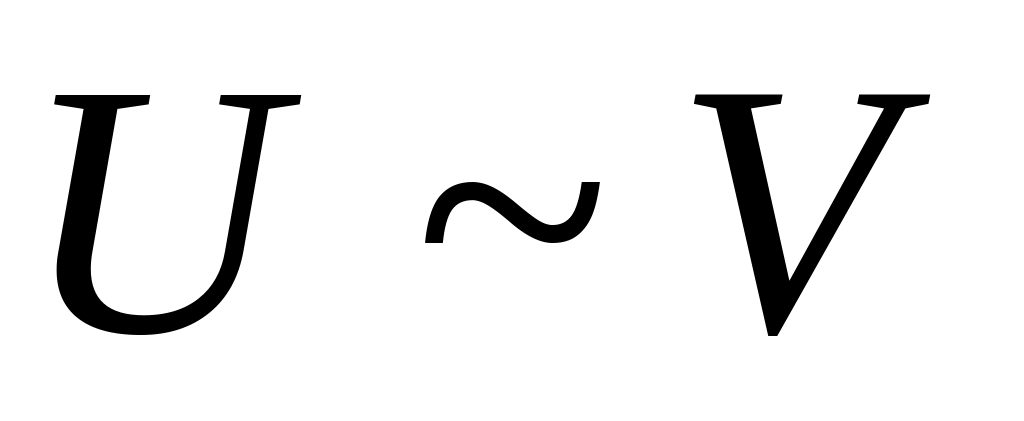 ,
і
т.д. також є формули.
,
і
т.д. також є формули.
Визначення не є формулою. Тільки умови 1 та 2 є формулами.
Функції
![]() та
та
![]() є еквівалентними, якщо вони приймають
однакові
істиностні значення при довільному
наборі істинних значень аргументів.
Якщо
є еквівалентними, якщо вони приймають
однакові
істиностні значення при довільному
наборі істинних значень аргументів.
Якщо
![]() , для довільних p,
q,
r…
то така формула є тавтологією.
Використовується тавтологія для
перевірки правильності роботи елементів
системи.
, для довільних p,
q,
r…
то така формула є тавтологією.
Використовується тавтологія для
перевірки правильності роботи елементів
системи.
Перетворення функцій та перевірка на їх еквівалентність здійснюється шляхом складанням відповідних таблиць істинності.
Існує інший спосіб – використати закони алгебри логіки. Кожен з них перевіряється за допомогою таблиць істинності, а потім використовується для спрощення формул.
Нагадаємо – що 0 – хибне висловлення , 1 – істинне.
