Числа Фібоначі, ряд Фібоначі, трикутник Паскаля.

к =0,1

121 к =0,1,2

1331 к =0,1,2,3

14641 к=0,1,2,3,4

15101051 к = 0,1,2,3,4,5

і т. д.

Тоді формула біному Ньютона.

Властивості розкладу бінома Ньютона та біноміальних коефіцієнтів.

1. Кількість доданків у розкладі

2. У кожному доданку сума показників рівна “n”, що - відповідає загальній розмірності елементів лівої частини.

3. Загальний член розкладу .

4. Коефіцієнти розкладу, рівновіддалені від його кінців, рівні між собою бо

5. Середній член розкладу при n=2р (парному) найбільший якщо ж

n=2р-1 (відсутній один, середній член) то найбільших доданків два однакових.

6. Сума усіх біноміальних коефіцієнтів

Доведемо. При

7. Сума біноміальних коефіцієнтів з парними k рівна сумі значень з непарними k. Тобто 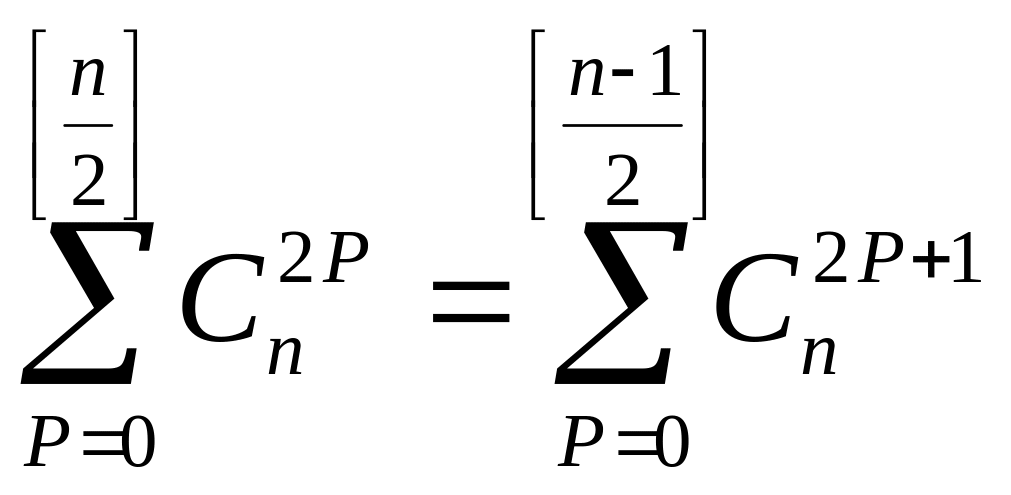де - ціла частина х.

Дійсно, якщо взяти та

Тоді . Якщо перенести від‘ємні коефіцієнти направо то отримаємо необхідне співвідношення.

Ряд Ньютона!

Повернемось до бінома Ньютона, який дає можливість записати вираз у вигляді розкладу по степеням а та х. Відмітимо, що дану формулу знали і до Ньютона (середньоазіатські вчені Омар Хайям, Гияседін та інші). В західній Європі до Ньютона її знав Паскаль. В чому ж заслуга Ньютона? В тому, що він розширив дану формулу на не цілі показники.

Саме він показав, що, якщо “а” додатне число і , то, для довільного дійсного значення , має місце рівність

Тобто, в цьому випадку ряд буде безмежним. Тільки при цілих в чисельнику буде момент, що появиться дужка =0: всі подальші члени розкладу пропадуть!

Розглянемо два практичних випадки реалізації.

1.

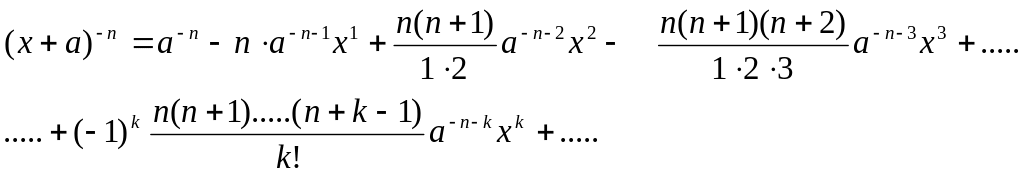
По іншому дану формулу можна переписати у виді

причому , адже

Це співвідношення можна довести методом індукції (самостійно Комбінаторика Н.Я. Виленкин ст..200.)

2. Розглянемо алгоритм обчислення квадратних коренів із заданих чисел, тобто у випадку коли ;

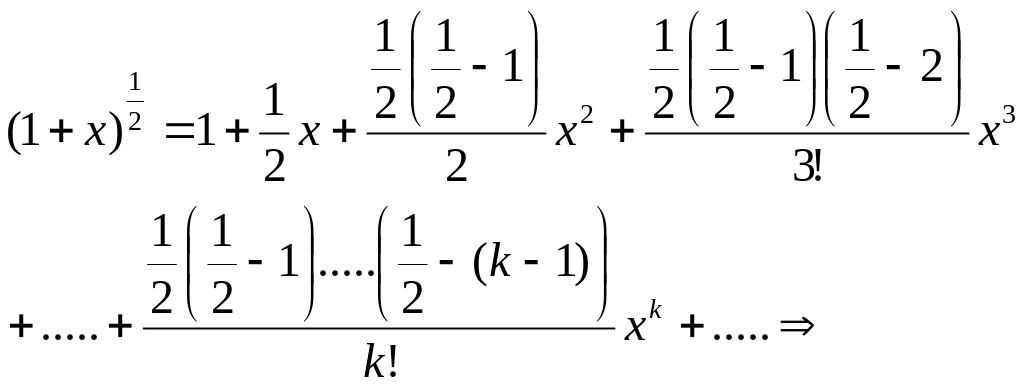
Цей вираз можна використати при обчисленнях кореня квадратного з раціональних чисел з любою точністю. Для цього досить винести з під кореня найбільше число, корінь якого відомий.

Наприклад.

а дальше ряд Ньютона

дозволить обчислити значення з довільною, бажаною степеню точності.

Перетворивши останній вираз, отримаємо

.

Це можна здійснити також і наступним способом

25

104. 5 00

4. 416

1087. 8 400

7. 7609

79100 і т.д.

От чому розклад в ряд по степенях b став називатись біномом Ньютона.

24