Основні властивості сполук:

1. при .

Дов..

2. .

Дов.

Розміщення перестановки та сполуки з повторенням.

До цих мір ми мали справу з вибірками, у яких елементи не повторювались. У комбінаторному аналізі є задачі, в яких елементи повторюються. Тобто ми маємо справу з к-вибірками з повторенням. При цьому вибірку кожного елемента здійснюють з повної множини .

Відмітимо, що вибірки з повтореннями можуть мати кількість елементів не тільки а і .

В залежності від змісту задачі вибірки з повтореннями можуть бути як впорядковані, так і невпорядковані. Тоді ми матимемо справу з розміщеннями, перестановками та сполуками з повтореннями.

Означення 1. Розміщенням із n по к з повторенням називається впорядкована к-вибірка із множини А, для якої .

Наприклад: Для множини

Розміщеннями з 4 по 5 будуть:

- і т.д.

В вибірках містяться кілька однакових елементів. Два розміщення вважаються різними якщо: відрізняються або видом елементів, або ж їх розміщенням.

Кількість різних розміщень з повторенням позначається . У розміщеннях з повтореннями кожен вибирається як один із елементів множини А, а оскільки їх “n” - то згідно правила добутку маємо .

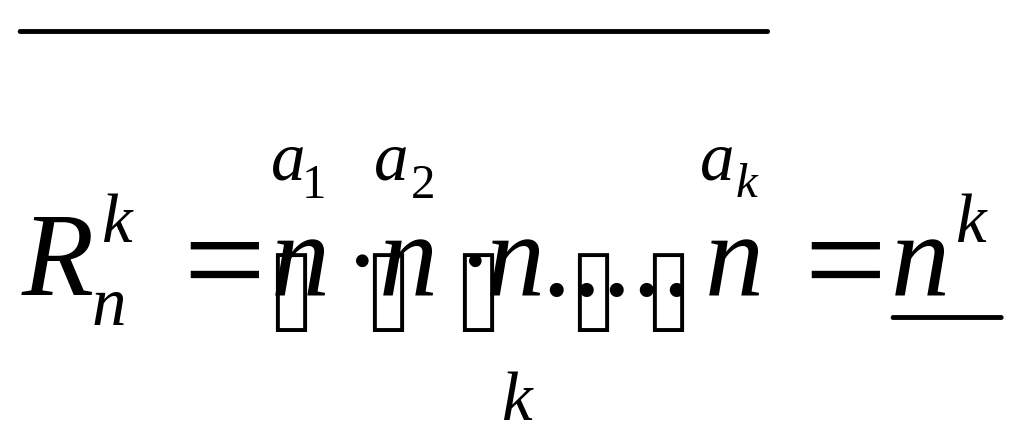Перестановки з повторенням.

Раніше перестановки були різними, якщо переставлялись два елементи множини (бо вони різні). Оскільки у нас вибірки містять однакові елементи то, здійснюючи перестановку ми можемо мати повторення послідовності (якщо переставили однакові елементи).

Раніше, коли елементи були різними, наприклад в слові мегаполіс 9 букв, довільні перестановки елементів приводили до зміни вибірки. В наведеному прикладі їх .У слові міссісіпі є 4-і, 3-с. Ясно, що якщо здійснити перестановки “і” то отримаємо 4! перестановок, що збігаються. Аналогічно для “с” їх 3!

Ясно, що число перестановок при умові, що вони різні буде менше у раз, а отже різних перестановок.

Узагальнимо дане положення.

Нехай для k різних типів предметів (елементів множини) необхідно обчислити кількість перестановок з елементів - першого типу, - другого, - 3-го і т.д. - того так, щоб . Такі перестановки називають перестановками з повторенням так як елементи у вибірках повторюються. Переставляючи однакові елементи ми отримаємо однакових перестановок. Якщо б усі елементи були різними то усіх можливих перестановок було б n! - повне число перестановок без повторів. Тоді, число різних перестановок з повторами можна обчислити за формулою

, де .

Наприклад: (Сполука.)

Нехай у нас є множина . Кожному елементу множини , що входить в сполуку, поставимо у відповідність 1, а елементам, що не входять поставимо “0”. Тоді будь-якій сполуці з “n” по “k” відповідає єдина “n” - перестановка з повторенням, що містить к-одиниць та n-к – нулів.

Тому . Ми отримали відомий вираз для обчислення кількості різних сполук.

Задача: Нехай в сигналі, який складається з кодового слова, що містить 18 кодових символів в трійковій системі числення є нулів -5; 1- 6; 2-7. Скільки різних кодових слів можна організувати з допомогою перестановки? Якщо б усі кодові символи були різними то їх кількість була б 18!.

Оскільки маємо перестановки з повтореннями то їх буде значно менше в раз, а отже, .

Задача 2. Скільки чотиризначних різних кодових послань можна здійснити передаючи числа із множини

Якщо числа різні, то їх

Якщо посилка містить 2 однакових числа, тоді їх кількість буде - кількість, де двійка виникає із-за наявності (1,1) та (3,3), - перестановки трьох вільних елементів, інших ніж вибрані. Іще є варіант кодового слова де співпадають два числа їх кількість буде .

Повна кількість різних кодових комбінацій буде

.

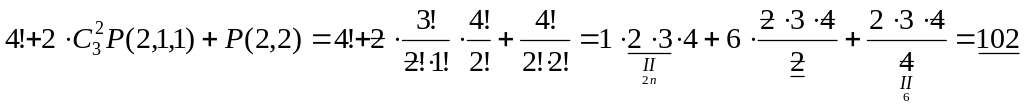Розглянемо задачу обчислення числа способів розташування n однакових предметів по m різних коробках.

Для цього закодуємо кожен розподіл з допомогою “0” та 1 наступним чином. Кожен предмет позначаємо одиничкою. Границю ящика позначаємо 0, при цьому враховуємо лише границі поділу предметів.

Наприклад. Обчислимо кількість роізних варіантів розміщення 12 предиетів по чотирьох ящиках. Приводимо один із можливих варіантів розміщення. Кількість предметів, що попали в І ящик 5 ,щоб відділити їх ставимо “0”. І так далі. Якщо ящик порожній, то на схемі будуть два нулі поруч (порожнім є 3-й ящик). В четвертому ящику є 1 елемент.

0 0 _ 0 12-1 1 2 3 4 m 3-0 Таким чином, комбінацією елементів 111110111111001 описується даний розподіл. Усіх елементів отримано 12+4-1=15.

Повну кількість різних розміщень отримаємо перестановками елементів з повторами, яка містить n-одиниць та m-1 – нулів. Це є код відповідного розміщення.

Пояснення методики обчислення на іншому прикладі.

4 ящики - 6 елементів. 3-й ящик порожній

0 0 0

Дане, конкретне, розміщення описується кодом-вибіркою 111011001. Тоді, обчислюючи кількість перестановок елементів у вибірці з повторами визначаємо число можливих розміщень n елементів по m ящиках.

За допомогою даного методу визначається кількість можливих розміщень.

Якщо ж необхідно визначити кількість різних варіантів, за умовою, щоб в кожному було обов’язково по одному предмету, то спочатку розкладемо по одному предмету в кожний ящик. Залишиться n –m об’єктів, які необхідно додатково розмістити по ящиках. Загальна кількість варіантів буде . Прикладом такого методу розміщення може служити телевізійний сигнал. І біт визначає початок нового кадру. Або ж, при зв’язку через послідовний порт, існують при кожній посилці стартові та стопові біти.

Сполуки (комбінації) з повторенням. Сполукою із n по к з повторенням називається невпорядкована к-вибірка з повторенням із множини А для якої . Кількість сполук позначається .

Приклади сполук з повторами.

Для множини можна створити сполуки і т.д. Для отримання формули, яка визначає кількість різних сполук скористаємось кодуванням, яке було розглянуто раніше.

Якщо сполуки були отримані з множини , то маємо елементи “n” типів. Кожній сполуці із n по к відповідає її код-перестановка з повторами яка містить k - одиниць та n-1 – нулів (дійсно нулі розміщаються лише між елементами , тому їх буде на 1 менше ніж груп). Один із прикладів розміщення

….

1 0 0 1 …01

одиничок “к”, нулів n-1. Тоді, обчисливши вираз

отримаємо загальну кількість відповідних сполук. Зауважимо, що способи розподілу “n” однакових елементів по m різних комірках – це задача на сполуки з повтореннями.

Якщо в сполуки з повтореннями обов‘язково повинні входити “r” фіксованих типів елементів, то спочатку їх заповнимо. Залишається n – r елементів, які необхідно розподілити по k коробках. Маємо сполук.

Біном Ньютона. Властивості біноміальних коефіцієнтів.

Розглянемо степені двохчлена де