
- •Розділ 2. Комбінаторний аналіз.
- •Загальні правила комбінаторики
- •Правило добутку
- •Розміщення.
- •Розміщення, перестановки і сполуки без повторень.
- •Загальна кількість різних перестановок.
- •Основні властивості сполук:
- •Перестановки з повторенням.
- •Числа Фібоначі, ряд Фібоначі, трикутник Паскаля.
- •Ряд Ньютона!
Розміщення, перестановки і сполуки без повторень.
З допомогою загальних правил комбінаторики можна розв’язувати різні задачі, при цьому виникають строго певні комбінації, яким присвоєно імена: розміщення, перестановки сполучення (комбінації).
Означення.
Скінчена множина
називається впорядкованою, якщо кожному
її елементу ставиться у відповідність
натуральне число “к”, яке означає
порядковий номер елементу в множині А
де
![]() де
де
![]() .
Якщо порядок елементів неістотній, то
множина називається невпорядкованою.
.
Якщо порядок елементів неістотній, то
множина називається невпорядкованою.
Розглянемо
підмножини
![]() ,
які утворюються за слідуючим правилом:
,
які утворюються за слідуючим правилом:
Перший крок
 вибираємо будь-який елемент
вибираємо будь-який елемент
 ;
із множини А
;
із множини АІз множини
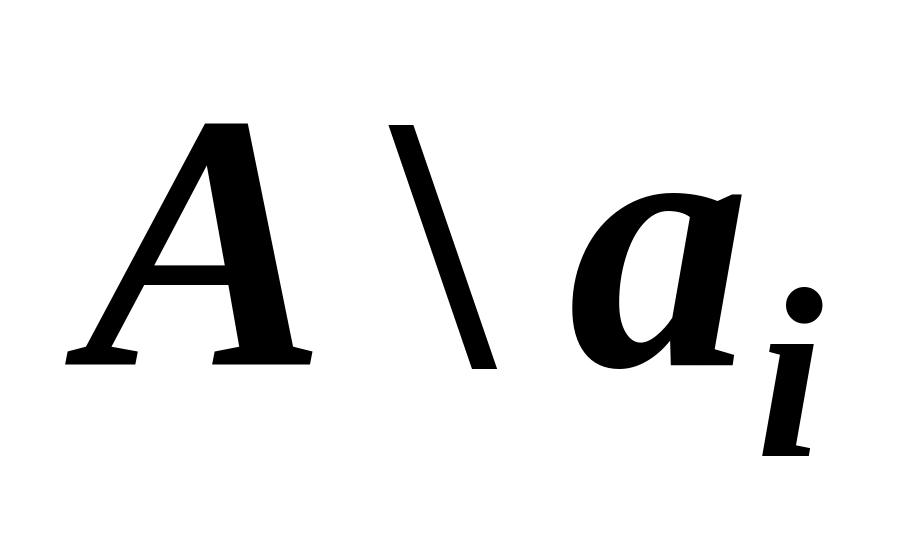 вибираємо
вибираємо
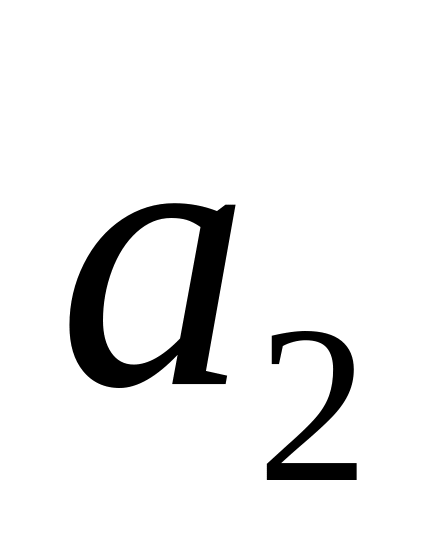
Із множини
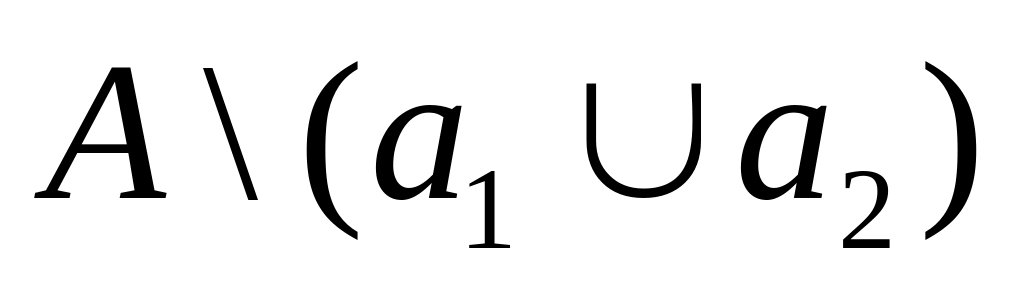 вибираємо
вибираємо
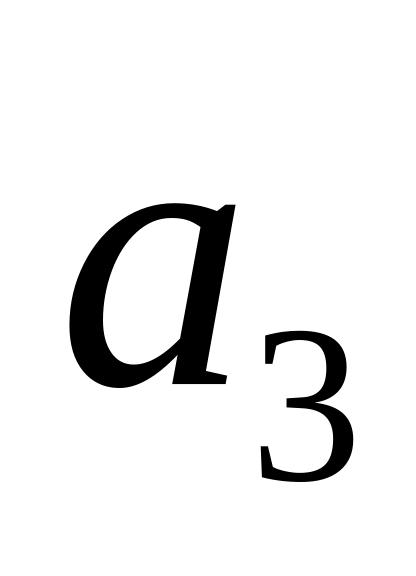
Із множини
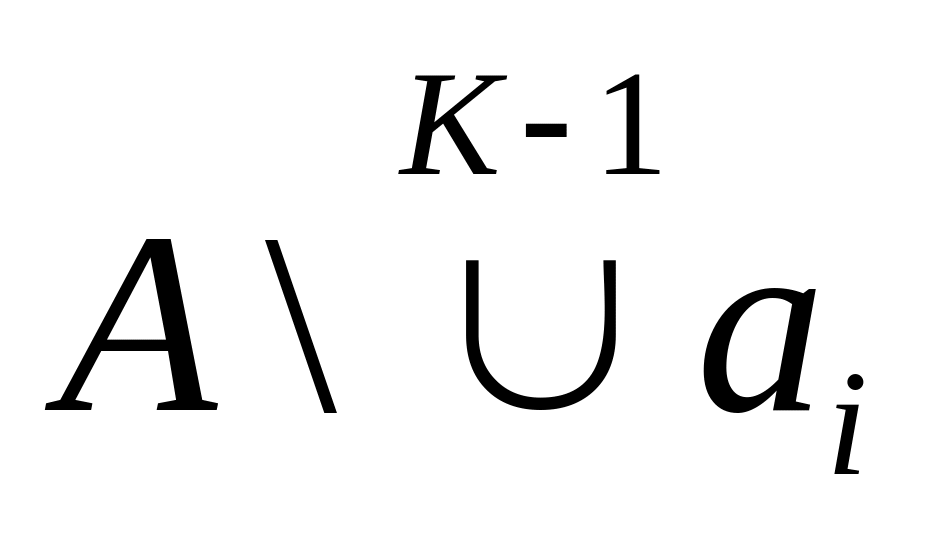 вибираємо
вибираємо
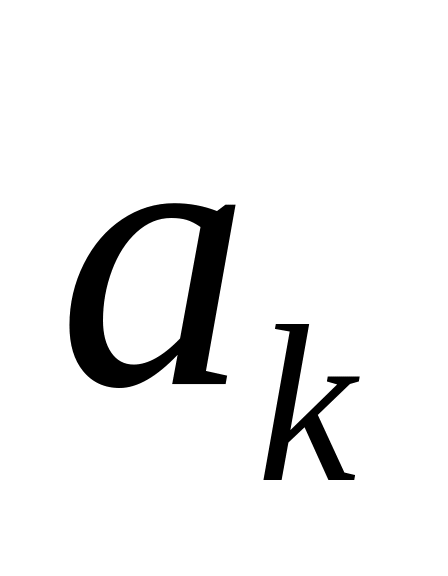
Із вибраних
елементів складаємо
![]()
![]() - це буде вибірка
без повторень, вона впорядкована, якщо
кожному вибраному елементу множини
- це буде вибірка
без повторень, вона впорядкована, якщо
кожному вибраному елементу множини
![]() поставити у відповідність номер. Отримали
впорядковану k
вибірку без повторів. А якщо елементам
множини
не присвоювати номери, то отримана
вибірка буде невпорядкованою, тобто
невпорядкована “k”
вибірка без повторів.
поставити у відповідність номер. Отримали
впорядковану k
вибірку без повторів. А якщо елементам
множини
не присвоювати номери, то отримана
вибірка буде невпорядкованою, тобто
невпорядкована “k”
вибірка без повторів.
Позначається
вибірка
![]() .
.
Якщо ж вибірку елементів брати з повної множини A весь час, то частина елементів буде повторюватись і стане “k” вибіркою з повторенням. Природньо, що отримана вибірка може бути як впорядкованою так і невпорядкованою.
Приклад з білетами, коли білет вибраний студентом вилучається (реалізується вибірка без повторів) і коли не вилучається – вибірка з повторами.
Означення 2.
Розміщення з “n”
по “к”
називається впорядкована “к”
вибірка без повторення із множини
А, для якої
![]() .
Загальна кількість різних розміщень
позначається
.
Загальна кількість різних розміщень
позначається
![]() .
.
Доведення. Переконаємось (див. кодіровку без повторень) в вірності співвідношення приведеного співвідношення.
На першому місці можна встановити один із “n” елементів множини, на другому – один із “n-1 “ елементів, що залишились.
![]()
Тому, очевидно,
що
![]() - згідно правила добутку.
Даний вираз
можна переписати у вигляді
- згідно правила добутку.
Даний вираз
можна переписати у вигляді
![]() де
де
![]()
![]() ;
;
![]() ,
зручному для користування.
,
зручному для користування.
Означення 3.
“n”
перестановкою називається впорядкована
n-мірна вибірка без повторень із множини
А,
причому
.
Позначається загальна кількість різних
вибірок
![]() .Ясно,
що будь-які n-перестановки
відрізняються лише порядком елементів,
і кожна вибірка містить усі елементи
множини А.
.Ясно,
що будь-які n-перестановки
відрізняються лише порядком елементів,
і кожна вибірка містить усі елементи
множини А.
Загальна кількість різних перестановок.
Зрозуміло, що
![]() бо вся сукупність різних вибірок може
бути обчислена за кількістю різних
розміщень із n
елементів по n.
бо вся сукупність різних вибірок може
бути обчислена за кількістю різних
розміщень із n
елементів по n.
![]() (очевидно).
(очевидно).
Означення 4.
Сполукою (або комбінацією) із “n”
елементів по
k
називається невпорядкована “к”
вибірка без повторень із множини А,
для якої
![]() і
і
![]() .
.
Позначаться
![]()
Доведення. Нехай
у нас n=3;
k=2.
Множина
А=![]() .
Набір вибірок, що містять два елемени
.
Набір вибірок, що містять два елемени
![]() .
Замітимо, що деякі вибірки містять одні
і тіж елементи (підкреслені), що, без
врахування порядку написання, повторюються
і повинні бути вилучені.
.
Замітимо, що деякі вибірки містять одні
і тіж елементи (підкреслені), що, без
врахування порядку написання, повторюються
і повинні бути вилучені.
Всього кількість різних вибірок 3.
Підрахуємо
![]() .
Обчислена різними методами загальна
кількість дає однаковий результат.
.
Обчислена різними методами загальна
кількість дає однаковий результат.
Доведемо
справедливість формули для випадку
![]() .
Для цього розіб’ємо всі можливі
розміщення
.
Для цього розіб’ємо всі можливі
розміщення
![]() на класи. В рамках одного класу розміщення
відрізняться лише перестановкою
елементів. Різні класи відрізняються
хоча б одним елементом. Тоді кожному
класу відповідає лише одна сполука
(число класів рівня
на класи. В рамках одного класу розміщення
відрізняться лише перестановкою
елементів. Різні класи відрізняються
хоча б одним елементом. Тоді кожному
класу відповідає лише одна сполука
(число класів рівня
![]() ).
Тоді, якщо виконати у вибірці усі можливі
перестановки, їх к!,
одержимо усі розміщення цього класу.
).
Тоді, якщо виконати у вибірці усі можливі
перестановки, їх к!,
одержимо усі розміщення цього класу.
Тобто
![]() Це підтверджує вірність формули. Ясно,
що число сполук які не містять жодного
елементу буде лише одна комбінація і
вибірка
Це підтверджує вірність формули. Ясно,
що число сполук які не містять жодного
елементу буде лише одна комбінація і
вибірка
![]()
![]()
