Розділ 2. Комбінаторний аналіз.

Вступ.

При розв’язуванні практичних задач виникають випадки, коли розглядаються взємозв’язок, комбінації елементів деякої скінченої множини.

Наприклад: скількома способами можна розсадити студентів по стільцях. Яка імовірність виграшу при заповненні однієї картки в “КЕНО” і т.д.

Розділ математики, в якому вивчається питання про число всеможливих комбінацій, що задовольняють тим чи іншим умовам, називається комбінаторикою.

Початок досліджень в даному розділі математики виконували в XVII ст. Тартальї, Паскаль, Ферма і в подальшому Бернулі, Лейбніц, Ейлер та інші. Це пов’язано в першу чергу із застосуванням комбінаторики в азартних іграх. За останні роки розвиток комбінаторики пов’язаний з розв’язуванням транспортних задач, складанням планів виробництва та реалізації продукції тощо.

Комбінаторика використовується в задачах лінійного програмуванні, статистики, для складання та декодування шифрів, при оцінці складності алгоритмів розв’язування задач в теорії інформації.

Загальні правила комбінаторики

Комбінаторика має справу із скінченими множинами і виникла як одна із теорій ігор.

Правило сум

Розглянемо потужність об’єднання двох множин

Якщо А і В є підмножинами множини С. так що

при чому , тобто кожен із об’єктів входить лише в одну множину. Тоді

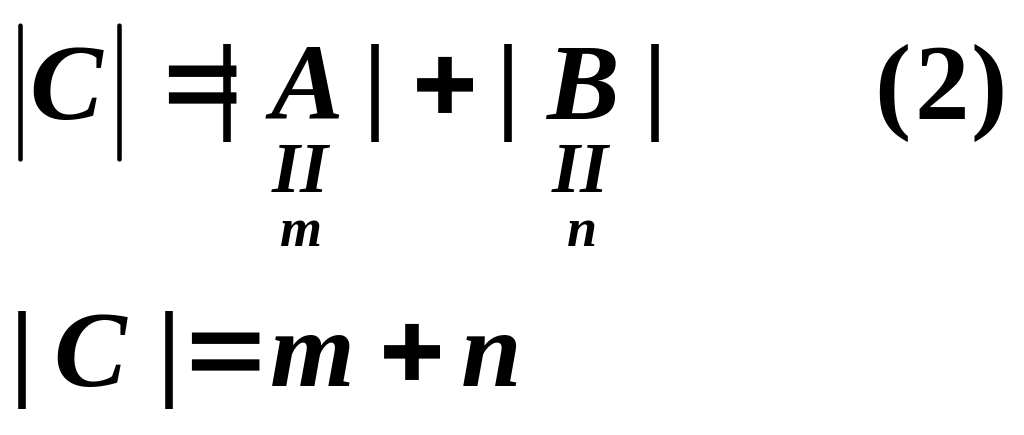
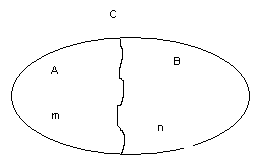
Формуліровка:

Якщо деякий об’єкт х А можна вибрати “n” способами, а другий об’єкт у В можна вибрати “m” способами то об’єкт або “x” або “у” можна вибрати m + n способами (якщо переріз множин .)

Правило сум може бути застосовано і для більшої ніж 2 кількості множин.

Правило добутку

Нехай нам необхідно розрахувати кількість пар (а в ) таких що а А; b В при чому |A| = n; |B| = m і елемент “в” вибирається після того, як вибрано елемент “а”.

Якщо тоді з очевидністю і т.д. ця кількість буде

Формуліровка:

Якщо об’єкт а можна вибрати n способами і після вибору а об’єкт b можна вибрати m способами, то вибір впорядкованої пари можна здійснити способами.

У деяких випадках необхідно обчислити число всеможливих способів вибрати впорядковані вибірки де і т.д. . Якщо потужність множин …, то загальна кількість можливих варіантів здійснення вибірки буде

Розміщення.

Приклад 1. Колесо велосипедиста після падіння має вигляд 8. Оскільки хазяїн Клубу – велосипедист, то здійснюється нову нумерація усіх квитків так, щоб число 8 у них не входило. Відомо, що число членів клубу тризначне число (як виявилось). Скільки членів клубу? Якщо допускається номер 0.0.0. (Розв’язок

Приклад 2: Система числення

В «n» – мірні системі числення використовується “n” чисел.

Скільки можна записати чисел, які записується “К” знаками.

. Використання тільки “n” чисел для кодування інформації приводить до так званих рівномірних кодів.

Одним з прикладів не рівномірного коду є Код Морзе. У ньому використовуються всього 2 символи: крапка та тире.

Однак довжина кодового слова різна.

Приклад 3 Яке найменше число знаків “∙” чи “–” повинна містити комбінація, щоб можна було передати довільну букву при використанні рівномірного коду? Виявляється, що 5 . Чому?

Одно позиційне число дає можливість передати лише 2 різні сигнали.

Двох позиційні - “4”. 3^х позиційні - “8”. 4^х позиційні “16”, це менше ніж вміст алфавіту української мови (30).

Тому телеграфний код, код Бодо, містить 5^ти - символьне слово – код, для передачі тексту.

Аналогічно можна розглянути спосіб обчислення об’єму алфавіту кодів для морського семафору, що містить комбінації- таких варіантів кодів цілком достатньо для передачі усіх букв. (Усіх 33.)

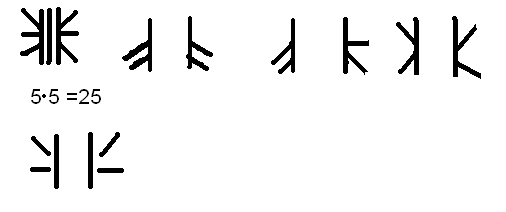
Приклад 4. Генетичний код.

Наслідкова інформація записується з допомогою різних порядків азотистих основ: аденін, тіамін, гуанін, цітазин. Ці основи встановлюють порядок будови білків організму із амінокислот, яких кількість порядку 20. Причому кожна амінокислота кодується з допомогою 3х чисел. Чому?

не досить для побудови усіх необхідних білків.

досить з надлишком для створення усіх білків.

Як же природа використовує даний надлишок коду невідомо?