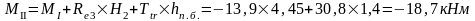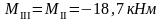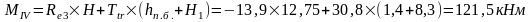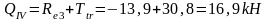§ Определение усилий в колоннах рамы

_{Статический расчёт поперечной рамы сделаем методом перемещений. При этом получим одно статически неопределимое неизвестное – горизонтальное перемещение плоской рамы на уровне верха колонн. Вводя по направлению неизвестного перемещения фиктивную связь, получим основную систему.}

_{Каноническое уравнение метода перемещений имеет вид:}

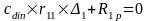
_{Основную систему подвергаем единичному воздействию неизвестного 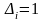и вычисляем реакции верхнего конца колонн.}

_{Для крайних колонн по оси "2" и "5":}

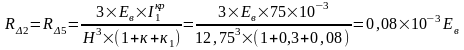
_{Для средних колонн по оси "3" и "4":}

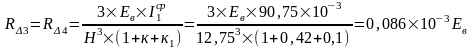
_{Суммарная реакция в фиктивной связи основной системы от единичного перемещения:}

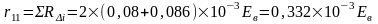
Усилия в колоннах рамы от постоянной нагрузки.

_{Колонна по оси "2".}

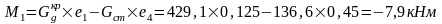
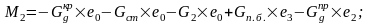
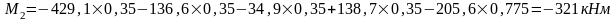
_{Вычислим реакцию в фиктивной связи верхнего конца колоны:}

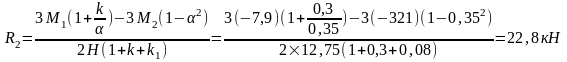
_{Колонна по оси "5".}

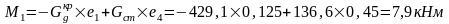
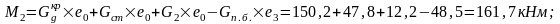
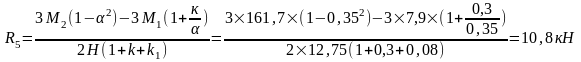
_{Колонны по оси "3" и "4" загружены центрально и для них R3= R4=0.}

_{Суммарная реакция фиктивных связей в основной системе:}

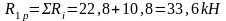
_{Из канонического уравнения метода перемещений следует, что:}

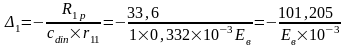
_{Упругая реакция колонн по оси "2" и "5":}

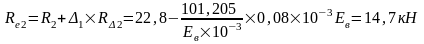
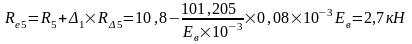
_{Упругая реакция колонн по оси "3" и "4":}

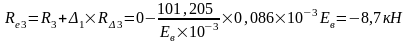
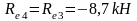
_{Изгибающие моменты и силы в сечениях колонны по оси "2":}

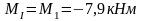
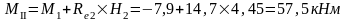
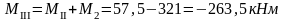
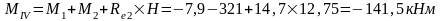
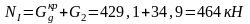
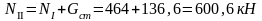
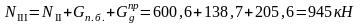
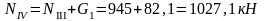
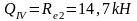
_{Изгибающие моменты и силы в сечениях колонны по оси "3":}

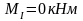
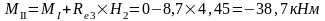
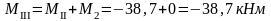
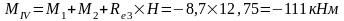
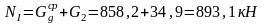
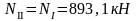
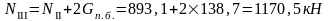
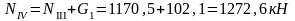
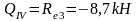
_{Изгибающие моменты и силы в сечениях колонны по оси "4" такие же, как и в сечениях колонны по оси "3".}

_{Изгибающие моменты и силы в сечениях колонны по оси "5":}

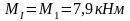
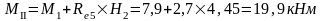
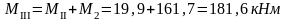
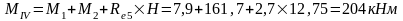
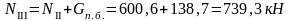
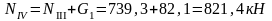
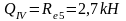
Усилия в колоннах рамы от снеговой нагрузки.

_{Колонна по оси "2".}

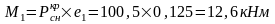
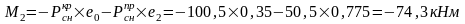
_{Вычислим реакцию в фиктивной связи верхнего конца колоны:}

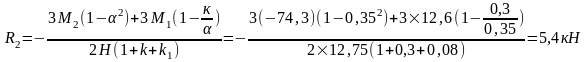
_{Колонна по оси "5".}

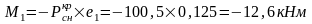
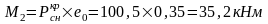
_{Вычислим реакцию в фиктивной связи верхнего конца колоны:}

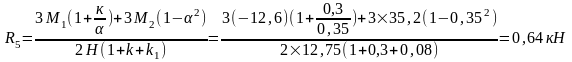
_{Колонны по оси "3" и "4" загружены центрально и для них R3= R4=0.}

_{Суммарная реакция фиктивных связей в основной системе:}

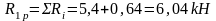
_{Из канонического уравнения метода перемещений следует, что:}

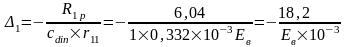
_{Упругая реакция колонн:}

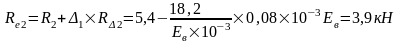
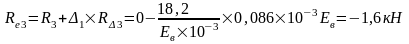
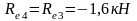
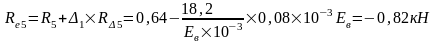
_{Изгибающие моменты и силы в сечениях колонны по оси "2":}

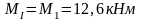
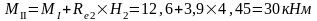
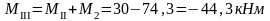
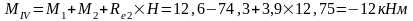
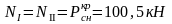
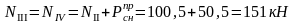
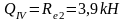
_{Изгибающие моменты и силы в сечениях колонны по оси "3":}

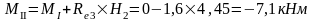
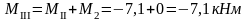
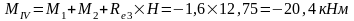
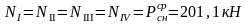
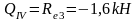
_{Изгибающие моменты и силы в сечениях колонны по оси "4" такие же, как и в сечениях колонны по оси "3".}

_{Изгибающие моменты и силы в сечениях колонны по оси "5":}

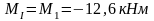
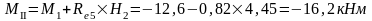
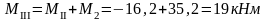
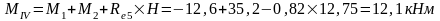
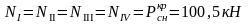
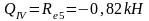
Усилия в колоннах рамы от крановых нагрузок

_{Рассмотрим следующие виды загружения:}

_{а) вертикальная крановая нагрузка от двух сближенных кранов Dmax на колонне по оси "2", Dmin - на колонне по оси "3". На колонне по оси "2" нагрузка Dmax=733,7 приложена с эксцентриситетом е3=0,35 м, аналогично эксцентриситету приложения нагрузки Gп.б.}

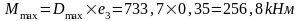
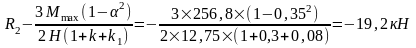
Одновременно на колонне по оси "3" действует сила Dmin с эксцентриситетом е=λ=0,75 м.

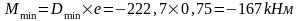
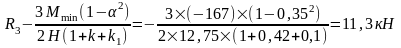
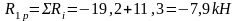
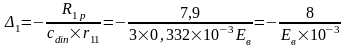
_{Упругая реакция колонн:}

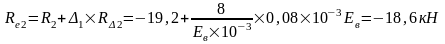
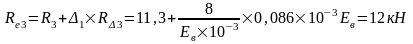
_{Изгибающие моменты и силы в сечениях колонны по оси "2":}

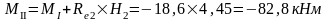
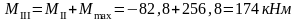
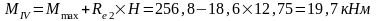
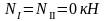
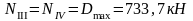
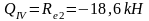
_{Изгибающие моменты и силы в сечениях колонны по оси "3":}

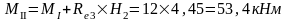
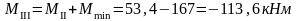
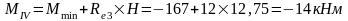
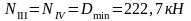
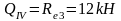
_{б) вертикальная крановая нагрузка от двух сближенных кранов Dmax на колонне по оси "3", Dmin – на колонне по оси "2".}

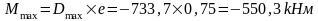
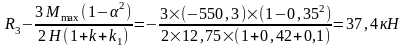
Одновременно на колонне по оси "2" действует сила Dmin с эксцентриситетом е3=0,35 м.

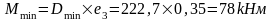
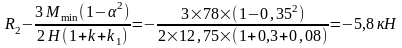
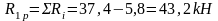
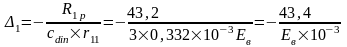
_{Упругая реакция колонн:}

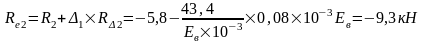
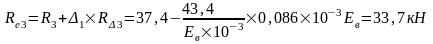
_{Изгибающие моменты и силы в сечениях колонны по оси "2":}

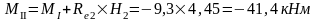
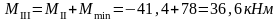
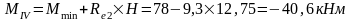
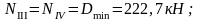
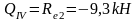
_{Изгибающие моменты и силы в сечениях колонны по оси "3":}

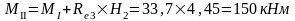
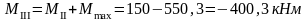
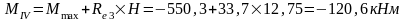
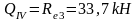
_{в) четыре крана с Dmax на колонне по оси "3": 2Dmax=1208,4 кН; Mmax=0; соответственно на колоннах по оси "2" и по оси "4" действует сила Dmin=222,7 кН.}

_{Колонна по оси "2":}

Колонна по оси "4"

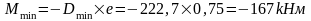
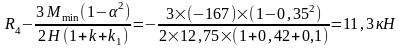
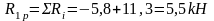
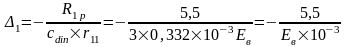
_{Упругая реакция колонн:}

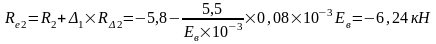
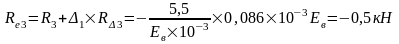
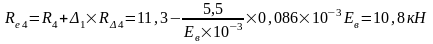
_{Изгибающие моменты и силы в сечениях колонны по оси "2":}

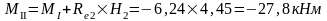
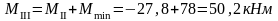
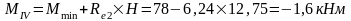
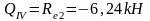
_{Изгибающие моменты и силы в сечениях колонны по оси "3":}

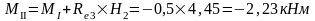
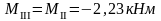
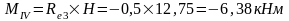
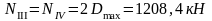
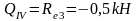
_{Изгибающие моменты и силы в сечениях колонны по оси "4":}

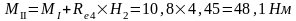
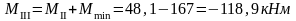
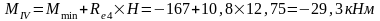
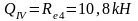
_{г) тормозная горизонтальная нагрузка на колонне по оси "2":}

_{Реакция в фиктивной связи колонны по оси "2" от Ttr=30,8 кН:}

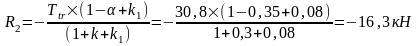
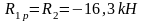
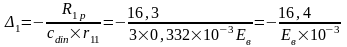
_{Упругая реакция колонн:}

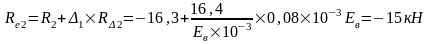
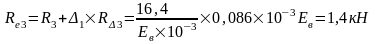
_{Изгибающие моменты и силы в сечениях колонны по оси "2":}

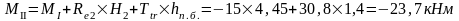
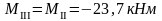
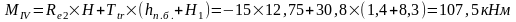
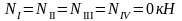
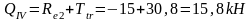
_{Изгибающие моменты и силы в сечениях колонны по оси "3":}

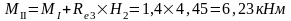
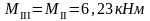
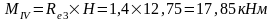
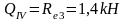
_{д) тормозная горизонтальная нагрузка Тtr на колонне по оси "3"}

_{Реакция в фиктивной связи колонны по оси "3" от Ttr=30,8 кН:}

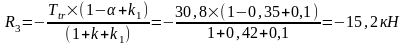
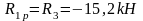
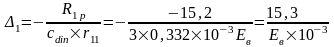
_{Упругая реакция колонн:}

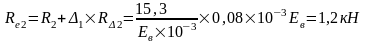
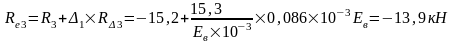
_{Изгибающие моменты и силы в сечениях колонны по оси "2":}

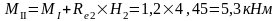
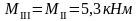
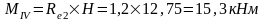
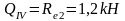
_{Изгибающие моменты и силы в сечениях колонны по оси "3":}