
- •Содержание:
- •Введение
- •Задание на проектирование:
- •Исходные данные:
- •1. Компоновка поперечной рамы.
- •3. Определение нагрузок на раму – блок:
- •3.1 Постоянные нагрузки:
- •На 1 колонну по крайнему ряду а:
- •На колонну среднего ряда б:
- •3.2 Снеговая нагрузка
- •3.3 Крановые нагрузки
- •3.4 Ветровые нагрузки
- •Статический расчёт рамы-блока
- •Составление расчётных сочетаний усилий
- •6.Расчет внецентренно нагруженного фундамента под среднюю двухветвевую колонну.
- •Расчет двухветвевой колонны среднего ряда.
- •8.Расчёт предварительно напряжённой двухскатной решётчатой балки покрытия.
- •Список использованной литературы
- •Пояснительная записка
8.Расчёт предварительно напряжённой двухскатной решётчатой балки покрытия.
8.1 Данные для проектирования:
Бетон класса В40 с
расчётными характеристиками при
коэффициенте условий работы бетона γb2
= 0,9:
 Обжатие
происходит при передаточной прочности
бетона
Обжатие
происходит при передаточной прочности
бетона
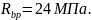 Расчётные
характеристики бетона для класса,
численно равного передаточной прочности
бетона при γb2
= 1:
Расчётные
характеристики бетона для класса,
численно равного передаточной прочности
бетона при γb2
= 1:

Предварительно
напрягаемая арматура стержневая класса
А – V
(
Ненапрягаемая
арматура класса А – III
(при d
< 10 мм
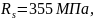 при d
≥ 10 мм
при d
≥ 10 мм
 и из обыкновенной арматурной проволоки
класса
и из обыкновенной арматурной проволоки
класса
 (при
Ø 5
(при
Ø 5


Геометрия балки
8.2 Расчётный пролёт, нагрузки, усилия
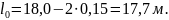
Масса балки 9,1 т, а погонная нагрузка от собственного веса балки:
 при
γf
=
1:
при
γf
=
1:
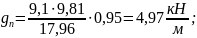
при γf > 1:

Нагрузку считаем равномерно распределённой по поверхности и собираем с полосы, равной шагу балок 12 м и суммируем с нагрузкой от веса балки.
Расчётная
схема балки и расположение расчётных
сечений:
Расчётная погонная нагрузка составляет:
при γf = 1:

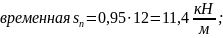



при γf > 1:

Для определения усилий в качестве расчётных сечений принимаем следующие:
0 – 0 – по грани опоры балки;
I – I – на расстоянии 1/6 пролёта от опоры;
II – II – в месте установки монтажной петли;
III – III – на расстоянии 1/3 пролёта от опоры;
IV – IV – на расстоянии 0,37 пролёта от опоры (опасное сечение при изгибе);
V – V – в середине пролёта.
Изгибающие моменты в сечениях определяем из выражения

где Q – поперечная сила на опоре;

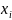 -
расстояние от опоры до i
– ого сечения;
-
расстояние от опоры до i
– ого сечения;
при γf = 1:


при γf > 1:

Изгибающие моменты в сечениях балки вычислены аналогично и приведены в таблице 5.
Сечение |
Х, м |
Моменты, кН · м |
||
γf = 1 |
γf > 1 |
|||
от продолжительной нагрузки |
от полной нагрузки |
от полной нагрузки |
||
0 – 0 |
0,15 |
58,3 |
68,85 |
83,4 |
I – I |
2,95 |
963,6 |
1137,9 |
1379 |
II – II |
3,95 |
1202,8 |
1420,45 |
1721,1 |
III – III |
5,9 |
1541,8 |
918,15 |
2206 |
IV – IV |
6,55 |
1671,3 |
1910,1 |
2313,9 |
V – V |
8,85 |
1734,4 |
2048,6 |
2480,9 |
8.3 Предварительный подбор продольной напрягаемой арматуры
Рассматриваем сечение IV – IV как наиболее опасное:
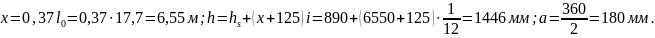
В
вернем поясе балки предусматриваем
конструктивную арматуру в количестве
4Ø12 А – III
(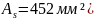 ;
а = 320/2 = 160 мм; в нижнем поясе – из 4Ø5 Вр
– I
(
;
а = 320/2 = 160 мм; в нижнем поясе – из 4Ø5 Вр
– I
(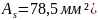 в виде сетки, охватывающей напрягаемую
арматуру.
в виде сетки, охватывающей напрягаемую
арматуру.
Рабочая высота сечения
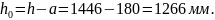
Граничная относительная высота сжатой зоны бетона:
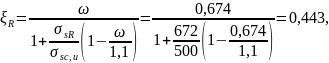
где



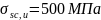 при
коэффициенте условий работы γb2
< 1.
при
коэффициенте условий работы γb2
< 1.
 Устанавливаем
положение границы сжатой зоны
Устанавливаем
положение границы сжатой зоны
 следовательно,
нижняя граница сжатой зоны проходит в
пределах верхнего пояса балки.
следовательно,
нижняя граница сжатой зоны проходит в
пределах верхнего пояса балки.
Вспомогательные коэффициенты:
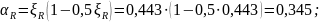

То есть сжатой арматуры достаточно;


Требуемая площадь сечения напрягаемой арматуры
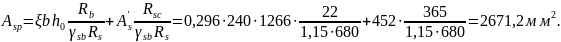
Принимаем напрягаемую арматуру в количестве 2Ø22 А – V + 4Ø25 А – V (Asp = 760 + 1963 = 2723 мм²), которую распределяем равномерно по периметру нижнего пояса балки.
8.4 Определение геометрических характеристик приведённого сечения.
1.
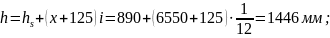
2. Площадь приведённого сечения:

где
 для
арматуры А – V;
для
арматуры А – V;
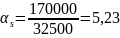 - для арматуры Вр
– I;
- для арматуры Вр
– I;
 для арматуры A
– III;
для арматуры A
– III;
Статический момент приведённого сечения относительно нижней грани:


Расстояние от центра тяжести сечения до нижней грани
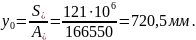
Момент инерции сечения относительно центра тяжести
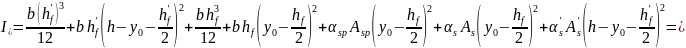
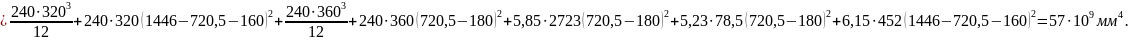
Момент сопротивления приведённого сечения для крайнего нижнего волокна
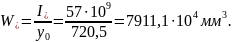
Упругопластический момент сопротивления сечения с отверстием для нижнего волокна.
Положение нулевой линии сечения при растянутой нижней зоне определим из условия:

где
 статический
момент площади бетона сжатой зоны
относительно нулевой линии;
статический
момент площади бетона сжатой зоны
относительно нулевой линии;

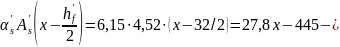 статический момент
площади арматуры сжатой зоны относительно
нулевой линии;
статический момент
площади арматуры сжатой зоны относительно
нулевой линии;
 статический момент
площади арматуры растянутой зоны
относительно нулевой линии;
статический момент
площади арматуры растянутой зоны
относительно нулевой линии;
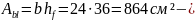 площадь растянутой
зоны в предположении, что х >
площадь растянутой
зоны в предположении, что х >
 .
.
 Из
указанного выше условия получим х =
68,92 см.
Из
указанного выше условия получим х =
68,92 см.
Упругопластический момент сопротивления для крайнего растянутого волокна
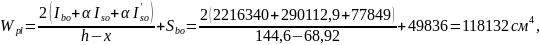
 где
где
 момент инерции площади сжатой зоны
относительно нулевой линии;
момент инерции площади сжатой зоны
относительно нулевой линии;
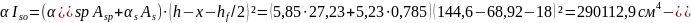 момент инерции
площади сечения арматуры растянутой
зоны относительно нулевой линии;
момент инерции
площади сечения арматуры растянутой
зоны относительно нулевой линии;

момент инерции площади сечения арматуры сжатой зоны относительно нулевой линии;
 статический момент
площади растянутого бетона относительно
нулевой линии.
статический момент
площади растянутого бетона относительно
нулевой линии.
Момент сопротивления приведённого сечения для крайнего сжатого волокна:
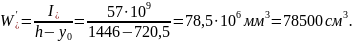
Положение нулевой линии сечения с отверстием при растянутой верхней зоне определяем по той же методике в предположении, что х > .
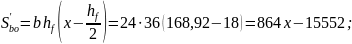

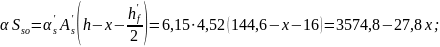
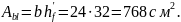
Получаем х = 44,86 см
>
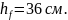
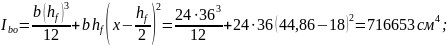


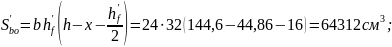

 8.5
Определение потерь предварительного
напряжения
8.5
Определение потерь предварительного
напряжения
Принятое предварительное напряжение должно находится в пределах
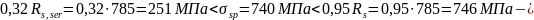 условие
выполняется.
условие
выполняется.
Вычисление потерь приведём на примере сечения IV – IV.
Первые потери
От релаксации напряжений стержневой арматуры при механическом способе натяжения

От температурного перепада

От деформации анкерных устройств

где Δl = 1,25 + 0,15 d = 1,25 + 0,15·25 = 5, l ≈ 20000 мм – длина натягиваемого стержня диаметром d.
Потери от быстронатекающей ползучести определяем в следующих местах по высоте поперечного сечения:
- на уровне центра тяжести напрягаемой арматуры, т. е. при
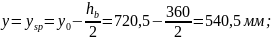
- на уровне крайнего сжатого волокна бетона, т. е. при

- на уровне центра тяжести сжатой арматуры, т. е. при
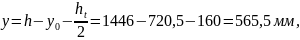
для чего вычисляем следующие параметры:
- усилие обжатия
 с учётом потерь σ1
…σ3 при
γsp
= 1
с учётом потерь σ1
…σ3 при
γsp
= 1
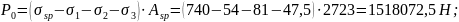
- напряжение в
бетоне на уровне арматуры

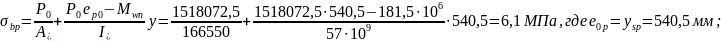
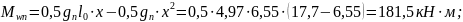
- то же на уровне
сжатой арматуры (

- то же на уровне крайнего сжатого волокна (у = 725,5 мм)
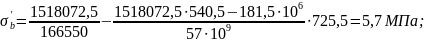
Коэффициент
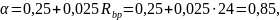 больше
нормированного значения 0,8, поэтому
принимаем α = 0,8.
больше
нормированного значения 0,8, поэтому
принимаем α = 0,8.
Для всех уровней
сечения отношение
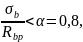 тогда
потери от быстронатекающей ползучести
соответственно составят:
тогда
потери от быстронатекающей ползучести
соответственно составят:
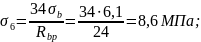
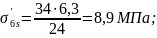
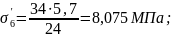
Итого первые потери

Предварительное напряжение с учётом первых потерь
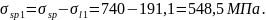
Усилие обжатия с учётом первых потерь
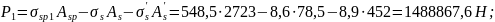
Эксцентриситет усилия Р1 относительно центра тяжести приведённого сечения
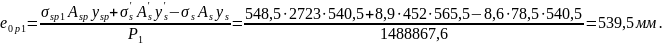
Вторые потери
От усадки бетона
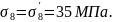
От ползучести бетона:


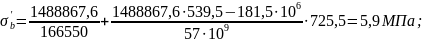
 При
При
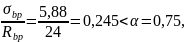 потери от ползучести бетона:
потери от ползучести бетона:
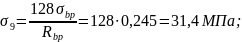
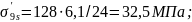

Итого вторые потери
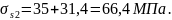
Полные потери
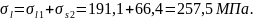

Усилие обжатия с учётом всех потерь

Эксцентриситет усилия P2


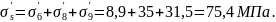
8.6 Расчёт прочности наклонных сечений
Так как фактическая
нагрузка на балку приложена в виде
сосредоточенных сил с шагом, равным
ширине плит покрытия 3 м, принимаем длину
проекции наклонного сечения с = 3 м
(расстояние от опоры до ближайшего
сосредоточенного груза). В опорном
сечении
 тогда в конце расчётного наклонного
сечения рабочая высота составит
тогда в конце расчётного наклонного
сечения рабочая высота составит
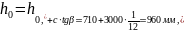
а средняя высота в пределах наклонного сечения

 Для
рассматриваемого наклонного сечения
(от грани опоры до первого сосредоточенного
груза) имеем:
Для
рассматриваемого наклонного сечения
(от грани опоры до первого сосредоточенного
груза) имеем:
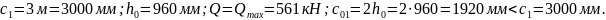




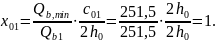
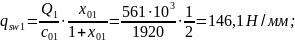
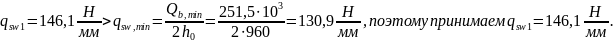
Максимально допустимый шаг поперечных стержней
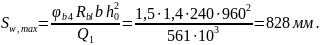
Принимаем на приопорном участке шаг поперечных стержней
 тогда требуемая площадь сечения хомутов
тогда требуемая площадь сечения хомутов
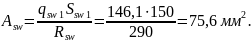
Принимаем в
поперечном сечении 2Ø7 А – III
( с шагом 150 мм.
с шагом 150 мм.
Выясним, на каком расстоянии от опоры шаг хомутов можно увеличить до 300 мм.
Фактическая интенсивность поперечного армирования
 для
шага
для
шага

 для
шага
для
шага
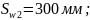

Задаём длину участка с шагом хомутов
 равной расстоянию
равной расстоянию
 от опоры до первого груза. Длину проекции
расчётного наклонного сечения принимаем
равной расстоянию от
от опоры до первого груза. Длину проекции
расчётного наклонного сечения принимаем
равной расстоянию от  опоры
до второго груза, т. е. с = 6 м >
опоры
до второго груза, т. е. с = 6 м >
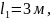 но меньше расстояния
но меньше расстояния
 от опоры до сечения с максимальным
моментом.
от опоры до сечения с максимальным
моментом.Рабочая высота в конце расчётного наклонного сечения

Длина проекции наклонной трещины в пределах рассматриваемого наклонного сечения
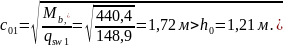
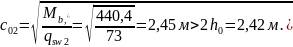
Поэтому принимаем

 При
При
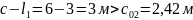 поперечная
сила, воспринимаемая хомутами:
поперечная
сила, воспринимаемая хомутами:

Поперечная сила, воспринимаемая бетоном в наклонном сечении:

Наибольшая поперечная сила от внешних нагрузок для рассматриваемого наклонного сечения:
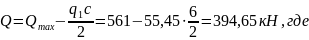

Проверяем условие прочности наклонного сечения
 то есть прочность
обеспечена.
то есть прочность
обеспечена.
Окончательно
принимаем на приопорных участках длиной
шаг
хомутов
 на остальной части пролёта шаг хомутов
на остальной части пролёта шаг хомутов
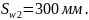
8.7 Проверка прочности нормальных сечений. Стадия изготовления и монтажа.
От совместного действия усилия обжатия P и собственного веса балки при подъёме возникают отрицательные изгибающие моменты, растягивающие верхнюю грань. Нагрузка от собственного веса принимается при коэффициенте надёжности γf = 1,1 с учётом коэффициента динамичности kd = 1,4 и условно считается равномерно распределённой

Изгибающие моменты, возникающие в местах расположения подъёмных петель
Нагрузка g1
только в
пролётах
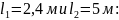

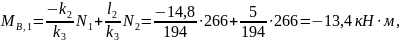
где фокусные отношения:

Нагрузка g1 только на консолях
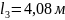
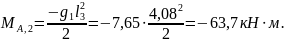
Для определения момента МВ используем метод фокусов:
Фокусные отношения


Момент на опоре В
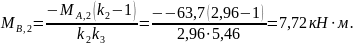
Суммарные изгибающие моменты:
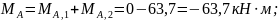
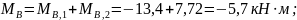
Расчётным является сечение II – II на опоре А; высота сечения h = 890 + 4080/12 = 1230 мм; рабочая высота при растянутой верхней грани составляет h0 = 1230 – 320/2 = 1070 мм.
Усилие обжатия вводится в расчёт как внешняя внецентренно приложенная сила N при коэффициенте точности натяжения γsp > 1

 Эксцентриситет
усилия обжатия
Эксцентриситет
усилия обжатия
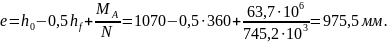
Расчётное сопротивление бетона в стадии изготовления и монтажа с учётом коэффициента условий работы


Граничная относительная высота сжатой зоны бетона

где
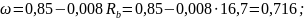

 при
коэффициенте условий работы γb2
> 1.
при
коэффициенте условий работы γb2
> 1.
Устанавливаем положение границы сжатой зоны
 граница
сжатой зоны проходит в пределах нижнего
пояса балки и сечение рассчитываем как
прямоугольное высотой h
= 1230 мм.
граница
сжатой зоны проходит в пределах нижнего
пояса балки и сечение рассчитываем как
прямоугольное высотой h
= 1230 мм.
Высота сжатой зоны

При
 несущая способность
несущая способность
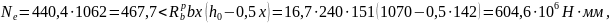 следовательно,
прочность сечения в этой стадии
обеспечена.
следовательно,
прочность сечения в этой стадии
обеспечена.
Стадия эксплуатации.
Проверяем прочность наиболее опасного сечения IV – IV, расположенного на расстоянии 0,37 l0 от опоры.
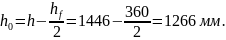
Граничная относительная высота сжатой зоны

где
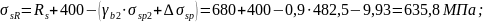

 ;
при
коэффициенте условий работы γb2
< 1.
;
при
коэффициенте условий работы γb2
< 1.
Устанавливаем положение границы сжатой зоны, принимая в первом приближении коэффициент
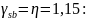

 граница сжатой
зоны проходит в пределах верхнего пояса
и расчёт выполняем как для прямоугольного
сечения высотой h
= 1446 мм.
граница сжатой
зоны проходит в пределах верхнего пояса
и расчёт выполняем как для прямоугольного
сечения высотой h
= 1446 мм.
Высота сжатой зоны при значении

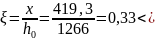
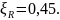
 принимаем
принимаем
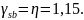
Предельный момент, воспринимаемый сечением IV – IV:
 то есть прочность
данного сечения обеспечена.
то есть прочность
данного сечения обеспечена.
8.8Расчёт по образованию нормальных трещин
В этом расчете следует проверить трещиностойкость балки при действии эксплуатационных нагрузок. Расчёт по образованию нормальных трещин производится из условия:

Mn
– изгибающий
момент от внешних нагрузок с коэффициентом
надёжности по нагрузке
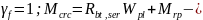 момент, воспринимаемый сечением при
образовании нормальных трещин; здесь
момент, воспринимаемый сечением при
образовании нормальных трещин; здесь
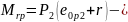 момент усилия обжатия относительно
ядровой точки сечения. Расчёт производим
на примере сечения IV
– IV.
Усилие обжатия Р2
= 1273,9 кН,
его эксцентриситет
момент усилия обжатия относительно
ядровой точки сечения. Расчёт производим
на примере сечения IV
– IV.
Усилие обжатия Р2
= 1273,9 кН,
его эксцентриситет

Максимальное напряжение в крайнем сжатом волокне бетона


 Коэффициент
Коэффициент
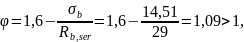 принимаем
φ = 1. Расстояние до наиболее удалённой
ядровой точки с учётом неупругих
деформаций сжатого бетона
принимаем
φ = 1. Расстояние до наиболее удалённой
ядровой точки с учётом неупругих
деформаций сжатого бетона
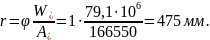
Момент образования трещин
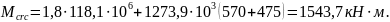
При
 в стадии эксплуатации на нижней грани
балки образуются нормальные трещины и
необходимо выполнить расчёт по их
раскрытию.
в стадии эксплуатации на нижней грани
балки образуются нормальные трещины и
необходимо выполнить расчёт по их
раскрытию.
8.9.Расчёт по раскрытию нормальных трещин. Стадия эксплуатации.
Рассматриваем
наиболее напряжённое сечение IV
– IV,
в котором действует усилие обжатия Р2
= 1273,9 кН с
эксцентриситетом
 и момент от полной нагрузки
и момент от полной нагрузки
 в том числе момент от продолжительно
действующей нагрузки
в том числе момент от продолжительно
действующей нагрузки
 высота сечения h
= 1446 мм, рабочая высота
высота сечения h
= 1446 мм, рабочая высота
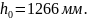
Определяем продолжительное раскрытие трещин от полной нагрузки:
Вспомогательные коэффициенты и параметры:
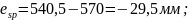
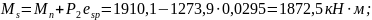
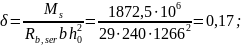




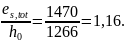
Относительная высота сжатой зоны в сечении с трещиной


 Плечо
внутренней пары сил в сечении с трещиной
Плечо
внутренней пары сил в сечении с трещиной

Напряжения растянутой арматуры с учётом коэффициента δ, равного:
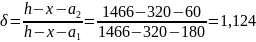
где
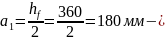 расстояние до центра тяжести всеё
растянутой арматуры нижнего пояса
балки;
расстояние до центра тяжести всеё
растянутой арматуры нижнего пояса
балки;
 то же до нижнего ряда стержней.
то же до нижнего ряда стержней.
Приращение напряжений в растянутой арматуре

Средний диаметр растянутой арматуры

Ширина непродолжительного раскрытия трещин

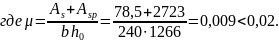
Определим непродолжительное (начальное) раскрытие трещин от продолжительно действующей нагрузки.
Высота сжатой зоны
 в данном случае не изменится, значит не
изменится и плечо пары сил z
= 1107 мм. Тогда приращение напряжений в
растянутой арматуре:
в данном случае не изменится, значит не
изменится и плечо пары сил z
= 1107 мм. Тогда приращение напряжений в
растянутой арматуре:

 Ширина
непродолжительного раскрытия трещин
от продолжительно действующей нагрузки:
Ширина
непродолжительного раскрытия трещин
от продолжительно действующей нагрузки:
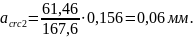
Определим продолжительное раскрытие трещин от продолжительно действующей нагрузки, для которой
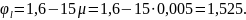
Тогда ширина продолжительного раскрытия трещин
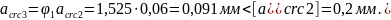
Полная (непродолжительная) ширина раскрытия трещин

8.10.Определение прогиба балки
Прогиб определяется от продолжительно действующих нагрузок (постоянных и временных длительно действующих).
Прогиб решётчатой балки приближённо определяем по формуле:
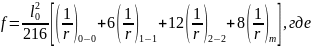
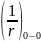 -
кривизна на опоре (сечение 0-0);
-
кривизна на опоре (сечение 0-0);
 -
кривизна в сечении на расстоянии
-
кривизна в сечении на расстоянии
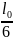 от опоры;
от опоры;
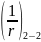 -
кривизна в сечении на расстоянии
-
кривизна в сечении на расстоянии
 от опоры;
от опоры;
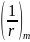 - кривизна в сечении посередине пролёта.
- кривизна в сечении посередине пролёта.

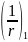 = 0 – кривизна от
кратковременных нагрузок;
= 0 – кривизна от
кратковременных нагрузок;
 кривизна от
постоянных и временных длительно
действующих нагрузок;
кривизна от
постоянных и временных длительно
действующих нагрузок;
 кривизна выгиба элемента от действия
усилия обжатия;
кривизна выгиба элемента от действия
усилия обжатия;
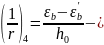 кривизна выгиба от усадки и ползучести
бетона при длительном действии усилия
предварительного обжатия. Здесь
кривизна выгиба от усадки и ползучести
бетона при длительном действии усилия
предварительного обжатия. Здесь
 относительные
деформации усадки и ползучести бетона
соответственно на уровне растянутой
арматуры и крайнего сжатого волокна
бетона
относительные
деформации усадки и ползучести бетона
соответственно на уровне растянутой
арматуры и крайнего сжатого волокна
бетона

Кривизны в расчётных сечениях вычислены по этим формулам и приведены в таблице:
-
Параметры
Величины параметров в сечениях
0 – 0
I – I
III – III
V – V

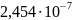


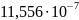
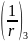
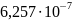
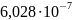





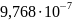

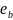
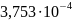
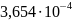

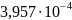
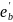
0
0

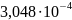
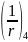
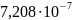

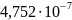
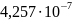

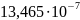



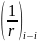


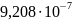
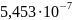
Прогиб балки от продолжительной нагрузки

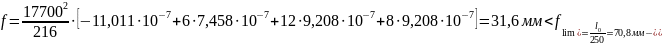 предельно
допустимый прогиб.
предельно
допустимый прогиб.
