6. Расчет двухветвевой колонны среднего ряда.

Данные для расчета сечений. Бетон тяжелый класса В15, под­вергнутый тепловой обработке при атмосферном давлении, R_b = 8,5 МПа; R_bt = 0,75 МПа; E_b=20,5·10³ МПа (прил. I н IV). Армату­ра класса А-ΙΙΙ, d >10 мм, R_s= R_sc=365 МПа, R_s=2·10⁵ МПа (прил. V). В данном примере ограничиваемся расчетом двух сечений: 2—2 и 4—4.

Сечение 2 – 2 на уровне верха консоли колонны. Сечение колонны b х h=50 x 60 см при а = а’ = 4 см; по­лезная высота сечения h₀=56 см. В сечении действуют три комбина­ции расчетных усилий:

Комбинации расчетных усилий
Усилия	Первая	Вторая	Третья
М, кН·м N, кН	250,4 1195,3	-117,3 862,8	0 1232,2

Усилия от продолжительного действия нагрузки М_l;=0; N_l = 862,8 кН.

При расчете сечения на первую и вторую комбинации усилий расчетное сопротивление R_b следует вводить с коэффициентом γ_b2=1,1, так как в комбинации включены постоянная, снеговая, крано­вая и ветровая нагрузки; на третью – с коэффициентом γ_b2= 0,9 (по­стоянная и снеговая). Расчет должен выполняться на все три ком­бинации, и расчетное сечение симметричной арматуры A_s=A’_s дол­жно приниматься наибольшее. Ниже дан расчет сечения по первой комбинации.

Вычисляем: e₀=M/N= 25040/1195,3=20,9 см; l₀=2H₂=2·4,4 = 8,8 м (в комбинации расчетных усилий учитывается крановая на­грузка); i = √h²/l2 = √60²/12 = 17,32 см; λ=l₀/i=880/17,32=50,8>14; необходимо учесть влияние прогиба элемента на его прочность.

Условная критическая сила (см. гл. IV)

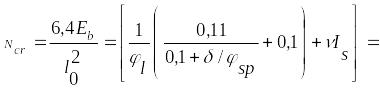
=56,92∙10⁵ Н = 5692 кН,

где I=bh³/12=50∙60³/12=900000 см⁴; φ_l=1+β(M_1l /M)=1+1∙224,33/561,18= 1,4; β= =1 (тяжелый бетон); M_1l = M_l + N_l(h₀ - а')/2 = 0+862,8(0,56 - 0,04)/2 = 224,33 кН∙м; M₁ = 250,4+1195,3(0,56 – 0,04)/2 = 561,18 кН∙м; δ=е₀/h=0,209/0,6=0,35; δ_min=0,5 – 0,01 (l₀/h) – 0,01R_bγ_b2=0,5 – 0,01 (880/60) – 0,01 ∙1,1∙8,5=0,26; δ<δ_min, принимаем δ = 0,26; v =E_s/ E_b = 200000/20500 =9,76; при μ=0,004 (первое приближение) I_s = μbh₀(0,5h – а)²=0,004∙50∙56∙(0,5∙60 – 4)²=7571,2 см⁴; φ_sp = 1.

Коэффициент η = l/(l – N/N_cr) = 1(1 – 1195,3/5692) = 1,27; расстояние e=e₀η+ +0,5h – a= 20,9*1,27 +0,5·60 – 4 = 52,54 см. При условии, что А_s=А _s ', высота сжатой зоны

см².

Относительная высота сжатой зоны ξ = x/h₀ = 25,6/56 = 0,46.

Граничное значение относительной высоты сжатой зоны бетона

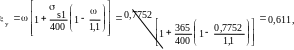
где ω=0,85 – 0,008 γ_b2 R_b=0,085 – 0,008∙1,1∙8,5 = 0,7752; σ_s1 = R_s=365 МПа.

Имеем случай ξ = 0,46 < ξ_y = 0,611;

Площадь арматуры A_S=A’_S назначаем по конструктивным сооб­ражениям, A_S=0,002bh₀= 0,002∙50∙56 = 5,6 см². Принимаем 3Ø16 с A_S=6,03 см².

Расчет сечения колонны 2 – 2 в плоскости, перпендикулярной к плоскости изгиба, не производим, так как l’₀/i₁=660/14,43=45,47< l₀/i₁=50,81, где l’₀= =l,5H₂ = l,5∙4,4=6,6 м; i_i√b²/12=50²/12= 14,43см.

Сечение 4 – 4 в заделке колонны. Высота всего сечения двухветвевой колонны 120 см; сечение ветви b x h =50 x 25 см; h₀=21 см; расстояние между осями ветвей с = 95 см; расстояние между осями распорок при четырех панелях s=H₁/n = 7,75/4 ≈ 1,94 м; высота сечения распорки 40 см. В сечении дейст­вуют три комбинации расчетных усилий, значения их приведены в табл.

Комбинации усилий

Усилия	Первая	Вторая	Третья
M, кН∙м N, кН Q, кН	289,35 1444,78 - 33,83	-409,56 1650,98 -23,24	-291,58 2271,41 29,8

Усилия от продолжительного действия нагрузки: M_l=0; N_l= 1045,18 кН; Q_i=0. Расчет должен выполняться на все три комби­нации усилий, и расчетное сечение арматуры A_s=A’_s должно прини­маться наибольшее. Ниже дан расчет по третьей комбинации.

Расчетная длина подкрановой части колонны при учете нагруз­ки от крана во всех комбинациях l₀=ψH₁=1,5∙7,75= 11,625 м. Приведенный радиус инерции сечения двухветвевой колонны в плоскости изгиба определяем по формуле:

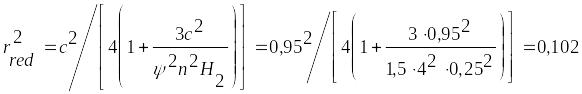см²;

r_red =√0,102 = 0,32 см.

Приведенная гибкость сечения λ_red =l₀/ r_red = 11,625/0,32=36,33 > 14 - необходимо учесть влияние прогиба элемента на его прочность.

Вычисляем: e₀ = 29158/2271,41 = 12,8 см; I = 2[bh³/12 + bh(c/2)²] =

=2[50∙25³/12+50∙25(95/2)²]=57,71. 10⁵ см⁴; M_1l = 0+1045,18(0,95/2)=496,5 кН∙м; M₁= 291,58 + 2271,41(0,95/2) = 1370,5 кН∙м; β=1; φ_l=1+ 1+496,5/1370,5=2,36; δ=12,8/120 = 0,11; δ_min = 0,5 – 0,01(1162,5/120) - 0,01∙1,1∙8,5=0,31; δ<δ_mjn, принимаем δ=0,31; v=9,77. Предварительно задаемся коэффициентом армирования μ = 0,0065 (первое приближение); I_s =2∙0,0065∙50∙25(95/2)²= =0,3666∙10⁵ см⁴.

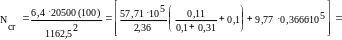
= 185,33∙10⁵ H = 18533 кН.

Коэффициент η = l (1—2271,41/18533) = 0,88.

Определяем усилия в ветвях колонны по формуле : N_br=N/2 ±Мη/с= =2271,41/2 ± 298,58*0,88/0,95=1135,7±270,1 кН;

N_br=1135,7 кН; N_b2= 865,6 кН.

Вычисляем: М_br= (Qs)/4= (29,8∙1,94)/4=14,5 кН∙м; е₀=14,5(100)/1135,7= 1,28 см>е_а=1 см: е_а≥1/30 h=25/30=0,833 см; е_а≥1/600l=

=194/600=0,32 см; е_а ≥1 см).

Т.к. е₀>е_а, в расчет вводим е₀ , тогда е= е_а+h/2 – а = =1,28+25/2 – 4 = 9,78 см.

Подбор сечений арматуры ведем по формулам:

Определяем:

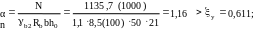
где

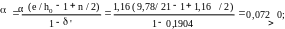
δ’=a’/h₀=4/21=0,1904.

Имеем расчетный случай ξ=1,01 > ξ_y=0,611. Армирование вет­вей принимаем симметричное. Вычисляем

=3,54 см².

Коэффициент армирования μ= (2*3,54)/50∙21 =0,01, что незна­чительно отличается от принятого ранее значения μ =0,0065∙2 = 0,013, поэтому второго приближения делать не требуется. При зна­чительном отклонении значения μ против заданного необходимо вы­полнить следующее приближение. Принимаем 3 Ø 14А-ІІІ с A_s=A’_s=4,62 см².

Проверим необходимость расчета подкрановой части колонны в плоскости, перпендикулярной к плоскости изгиба.

Расчетная длина l₀=0,8H₁ = 0,8∙7,75=6,2 м. Радиус инерции i=√50²/12= 14,43 см, l₀/i=620/14,43 = 42,97 > λ_red=36,33 – расчет не­обходим, необходимо учесть влияние проги­ба элемента на его прочность.

Значение случайного эксцентриситета: e₀≥ h/30=25/30=0,883 см; е_а≥ 1/600 H= =775/600= 1,29 см; е_а≥1 см. Принимаем е_а=1,3 см. Тогда е = 1,3+0,5(46–4)= =22,3 см; М_1l = 0+1045,18∙0,223 = 233,1 кН∙м; М₁= 0 + 2271,41∙0,223=506,5 кН∙м; β=1; φ_l =1 +233,1/506,5 = 1,46; δ = 1,3/60 = 0,021 < δ_min=0,5–0,01∙620/50- -0,01∙1,1∙8,5=0,286; I=2(25∙50³/12)=5,21∙10⁵ см⁴; I_s=2*10,18*(50/2—4)²=0,0898∙10⁵ см⁴ при A_s=A’_s = 10,18 см² – 4 Ø 18 А-ІІІ;

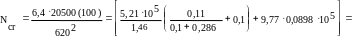
=47,25∙10⁵ H=4725кН; η =1/(1–2271,41/4725)=1,93; е=1,3∙1,93+50/2-4=23,5 см.

Определяем:

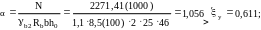δ’=4/46=0,087;

При

имеем расчетный случай ξ=0,964>ξ_у=0,611. Армирование ветвей принимаем симметричное. Вычисляем

= 8,62 см² < 10,18 см².

следовательно, принятого количе­ства площади арматуры достаточно.

Расчет промежуточной распорки. Изгибающий момент в распор­ке М_ds=(Qs)/2=

=(29,8∙1,94)/2=28,9 кН∙м. Сечение распорки прямо­угольное: b=50 см; h=40 см; h₀ = 36 см. Так как эпюра моментов двузначная

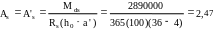см²,

принимаем 3 Ø 16 А-ІІІ с A_s =6,03 см².

Поперечная сила в распорке

Q_ds= (2M_ds)/c = (2∙28,9)/0,95 = 60,8 кН.

Определяем:

Q = φ_b4 γ_b2R_bt bh₀ = 0,6∙1,1∙0,75 (100) 50∙36 = 0,81∙10⁵ Н =81 кН, где φ_b4 =0,6.

Так как Q=81 кH> Q_ds =60,8 кН, поперечную арматуру прини­маем конструктивно d_w,=6 мм класса A-I c s = 150 мм.