Тема 5 Задачи оптимизации
Поиск минимума функции y=f(x) на интервале [a, b] на Scilab
Функция [f,xopt]=optim(costf,x0) возвращает локальный минимум функции costf.
Функция возвращает минимум функции (значение f) и точку, в которой этот минимум достигается (xopt).
Главной особенностью функции optim является структура функции costf, которая должна быть такой:
function [f,g,ind]=costf(x,ind)
f=gg(x);//функция, минимум которой мы ищем
g=numdiff(gg,x); //градиент функции f
endfunction
Если возвращаемое сформированной функцией costf значение ind равно 2, 3 или 4, то функция costf обеспечивает поиск минимума, т.е. в качестве результата функции optim возвращается f и xopt. Если ind=1, то в функции optim ничего не считается, условие ind<0 означает, что минимум f(x) не может быть оценен, а ind=0 прерывает оптимизацию. Вообще говоря, значение параметра ind является внутренним параметром для связи между optim и costf, для использования optim необходимо помнить, что параметр ind должен быть определен в функции costf.
Пример:
найти минимум функции
.
Решение. Построим график функции для определения интервалов [a, b], на которых находятся экстремумы этой функции.
-->x=-3:.1:3; y=x.^4-3*x.^2-5*x-4; plot(x, y); xgrid()
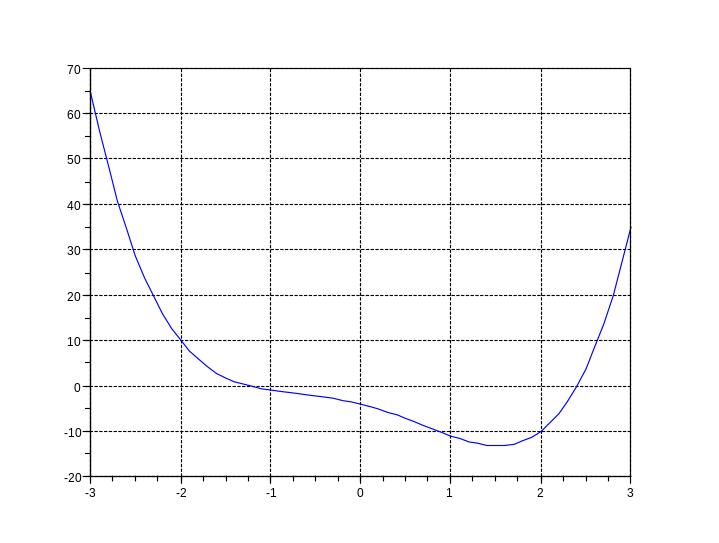
Из графика видно, что это отрезок [1, 2]. Набираем в окне редактора и отправляем на выполнение файл
function [f,g,r]=z(x,r)
f=x.^4-3*x.^2-5*x-4
g=4*x.^3-6*x-5
endfunction
x0=1;
[fmin,xmin]=optim(z,x0)
Получаем
--> xmin =
1.5233402
fmin =
- 13.193373
Возможен другой вариант, без ручного вычисления производной:
function y=gg(x)
y=x.^4-3*x.^2-5*x-4;
endfunction
function [f,g,r]=z(x,r)
f=gg(x)
g=numdiff(gg,x)
endfunction
x0=1;
[fmin,xmin]=optim(z,x0)
xmin =
1.5233402
fmin =
- 13.193373
xbasc()
clc
//Функция, вычисляющая разность между экспериментальными
//и теоретическими значениями,
//перед использованием необходимо определить
//z=[x;y] - матрицу исходных данных и
//с - вектор начальных значений коэффициентов,
//размерность вектора должна совпадать
//с количеством искомых коэффициентов
function y=G(c,z)
y=z(2)-c(1)-c(2)*z(1)
endfunction
//Исходные данные
x=[2 3 5 7];
y=[8 5 3 1];
//Формирование матрицы исходных данных
z=[x;y];//та же буква, что и в функции y=G(c,z)
//Вектор начальных приближений
c=[0;0];//нулей столько, сколько искомых коэффициентов. Это нач. приближение
//Решение задачи
[a,err]=datafit(G,z,c)
//Построение графика экспериментальных данных
plot2d(x,y,-4);
//Построение графика подобранной функции на отрезке [0 , 3]
t=2:0.01:7;
Ptc=a(1)+a(2)*t;
plot2d(t,Ptc);
err =
1.6271186
a =
9.7966103
- 1.3050848
