Тема 1. Решение уравнений

Для решения уравнений, в том числе трансцендентных, в Scilab применяют функцию fsolve(x0,f)

где x0 - начальное приближение, f - функция, описывающая левую часть уравнения f(x)=0.

Пример: решить уравнение

Набираем в окне редактора файл:

function y=f(x)

y=7*x.^3+45*x.^2+12*x+23;

endfunction

и сохраняем его под именем f.sci. Загружаем его в Scilab (Execute/Load into Scilab).

Для нахождения отрезка [a, b], на котором отделен корень данного уравнения, построим график функции .

-->x=-8:0.1:-5; plot(x, f(x)); xgrid()

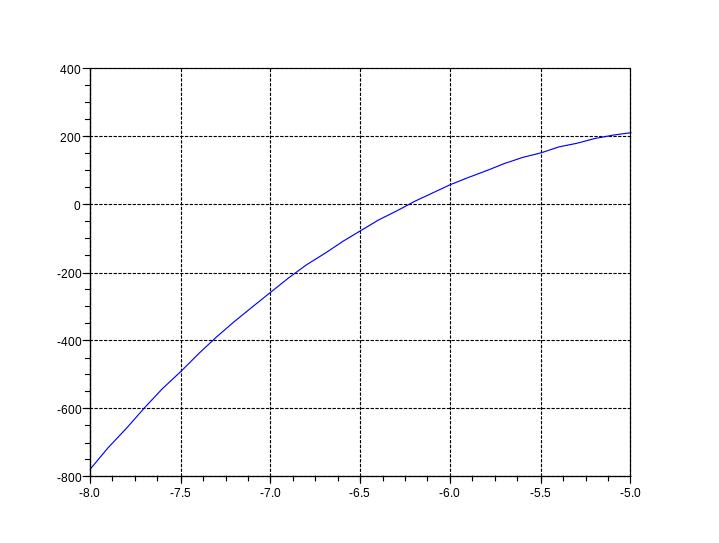
Из графика видно, что корень отделен на отрезке [-6.5 , -6]. Найдем его, используя функцию fsolve:

-->x0=-6.5;x1= fsolve(x0,f)

Получаем:

x1 =

- 6.2381997

Тема 2. Аппроксимация. Мнк

Пример. x=[0 1 2 3]; y=[-1.2 -0.1 1.3 1.8]. Построить уравнение аппроксимирующей параболы

Для этого используется функция datafit.

xbasc()

clc

//Функция, вычисляющая разность между экспериментальными

//и теоретическими значениями,

//перед использованием необходимо определить

//z=[x;y] - матрицу исходных данных и

//с - вектор начальных значений коэффициентов,

//размерность вектора должна совпадать

//с количеством искомых коэффициентов

function y=G(c,z)

y=z(2)-c(1)-c(2)*z(1)-c(3)*z(1)^2

endfunction

//Исходные данные

x=[0 1 2 3];

y=[-1.2 -0.1 1.3 1.8];

//Формирование матрицы исходных данных

z=[x;y];//та же буква, что и в функции y=G(c,z)

//Вектор начальных приближений

c=[0;0;0];//нулей столько, сколько искомых коэффициентов. Это нач. приближение

//Решение задачи

[a,err]=datafit(G,z,c)

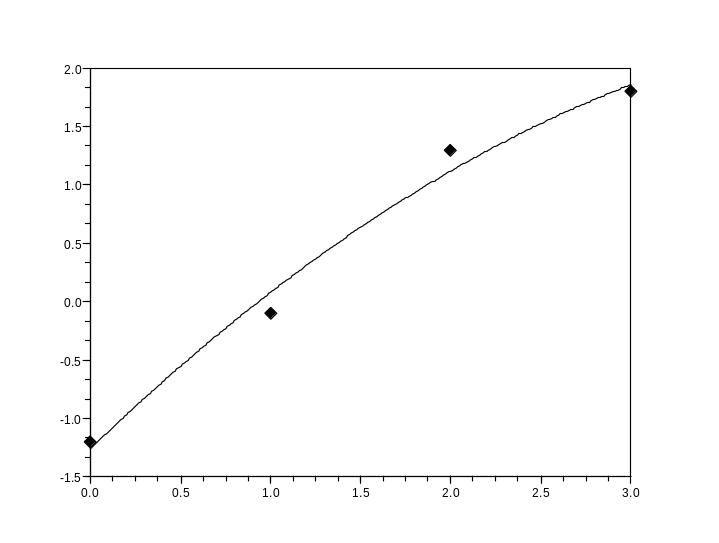
//Построение графика экспериментальных данных

plot2d(x,y,-4);

//Построение графика подобранной функции на отрезке [0 , 3]

t=0:0.01:3;

Ptc=a(1)+a(2)*t+a(3)*t^2;

plot2d(t,Ptc);

err =

0.072

a =

- 1.2600001

1.4900003

- 0.1500001

Здесь err - сумма площадей квадратов отклонений, а – вектор искомых коэффициентов с₀, с₁ и с₂ .

Аппроксимация. Метод средних точек.

Выбрать вид и определить параметры выбранной зависимости для функции

x=[5 7 9 11 13];y=[2.5 4.9 8 12.1 16.9];

Первую часть задачи можно решить, построив график на Scilab.

clc

xbasc()

x=[5 7 9 11 13];y=[2.5 4.9 8 12.1 16.9];

n=length(x);

xap=(x(1)+x(n))/2

xgar=2*x(1)*x(n)/(x(1)+x(n))

xgeo=(x(1)*x(n))^.5

yap=(y(1)+y(n))/2

ygar=2*y(1)*y(n)/(y(1)+y(n))

ygeo=(y(1)*y(n))^.5

t=[xgeo xap xap xgeo xgar xgar]

z=[ygeo ygeo ygar yap yap ygar]

plot(x,y)

plot(t,z,'*')

for i=1:6

xnumb(t(i),z(i),i)

end

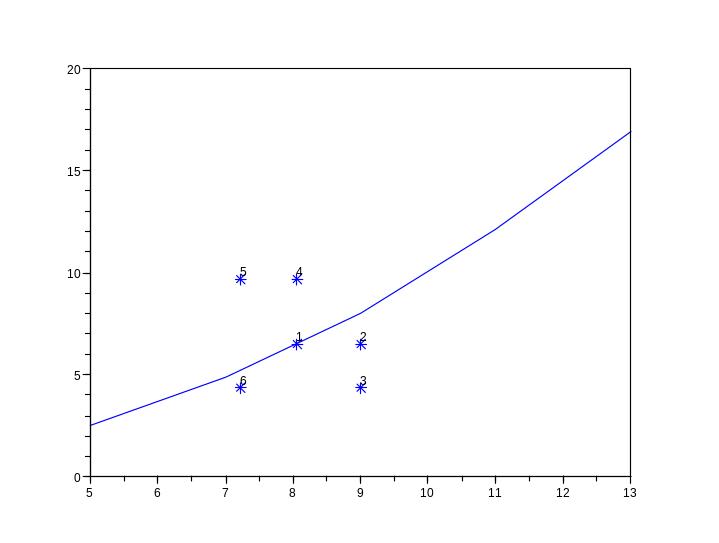
Из графика видно, что ближе всего к экспериментальной кривой точка с номером 1. Она соответствует кривой .

. Покажем, как найти неизвестные коэффициенты a и b на Scilab.

clc

xbasc()

function [zr]=F(c,z)

zr=z(2)-(c(1)*z(1)^c(2))

endfunction

x=[5 7 9 11 13];

y=[2.5 4.9 8 12.1 16.9];

z=[x;y];

c=[1;1];

[d,S]=datafit(F,z,c)

t=min(x)-.1:.01:max(x)+.1;

Yt=(d(1)*t^d(2));

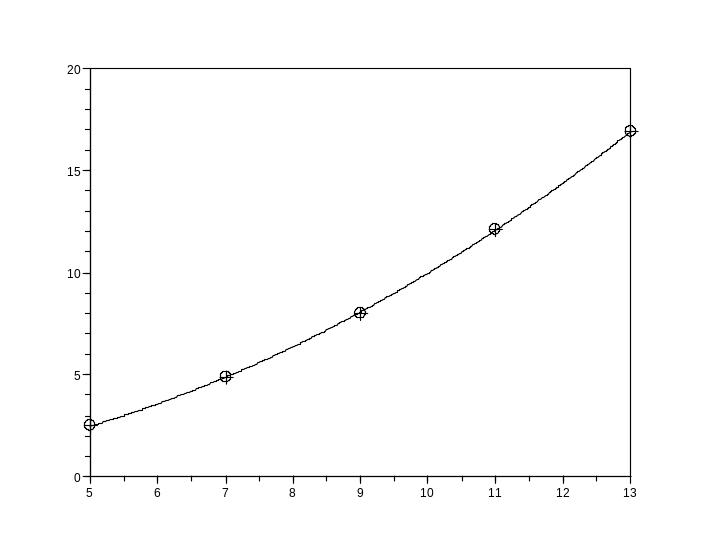
plot2d(x,y,-3);

plot2d(t,Yt);

S = 0.0067979

d =

0.0973802

2.0102774

В ответе d(1)= 0.0973802 это a, d(2)= 2.0102774 это b.

Таким образом, уравнение кривой, полученной на scilab,

x	y
5	2.5	2.464
7	4.9	4.846
9	8	8.032
11	12.1	12.022
13	16.9	16.819