2.4. Векторное пространство

2.4.1. n-МЕРНЫЙ ВЕКТОР И ВЕКТОРНОЕ ПРОСТРАНСТВО

Определение. n-мерным вектором называется упорядоченная совокупность n действительных чисел (x₁, x₂,…, x_n). Числа x₁, x₂,…, x_n называются компонентами вектора .

Определение. n-мерным векторным пространством R_n называют совокупность n-мерных векторов с действительными компонентами, рассматриваемая с определенными в ней операциями сложения векторов и умножения вектора на число.

2.4.2. Размерность и базис векторного пространства

Вектор называется линейной комбинацией векторов , если существуют такие действительные числа , не все одновременно равные нулю, что имеет место равенство .

Введем два эквивалентных определения линейной зависимости векторов.

Определение. Система векторов (k > 1) пространства R_n называется линейно зависимой, если хотя бы один из этих векторов является линейной комбинацией остальных векторов. В противном случае система векторов называется линейно независимой.

Определение. Система векторов (k > 1) пространства R_n называется линейно зависимой, если существуют такие числа , хотя бы одно из которых отлично от нуля, что имеет место равенство: . В противном случае система векторов называется линейно независимой.

Пример 2.13. Выяснить, является ли данная система векторов линейно зависимой.

.

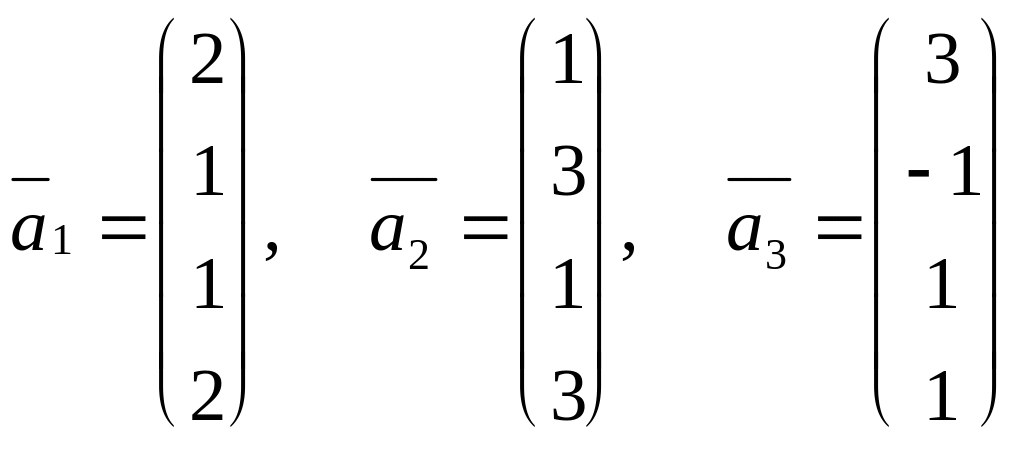Решение. Найдем решение эквивалентного равенства :

.

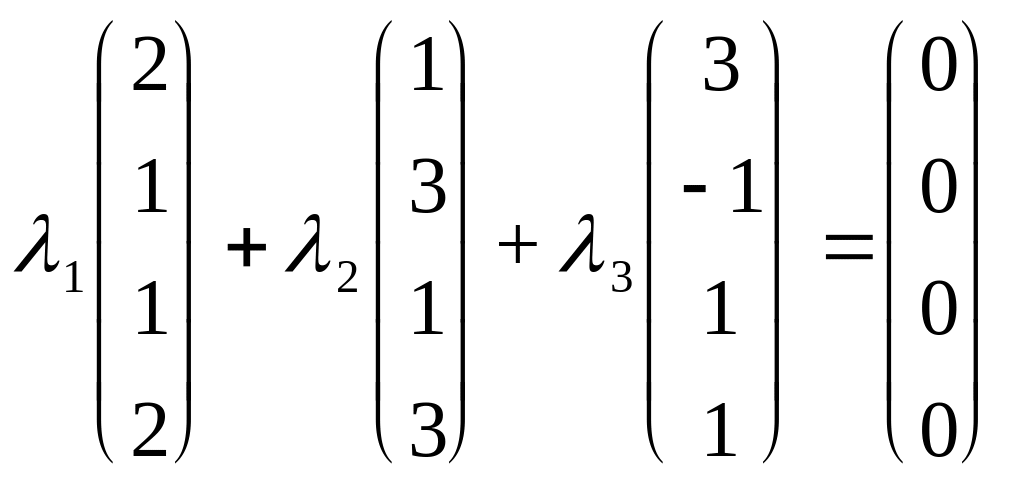Задача сводится к решению однородной системы линейных уравнений

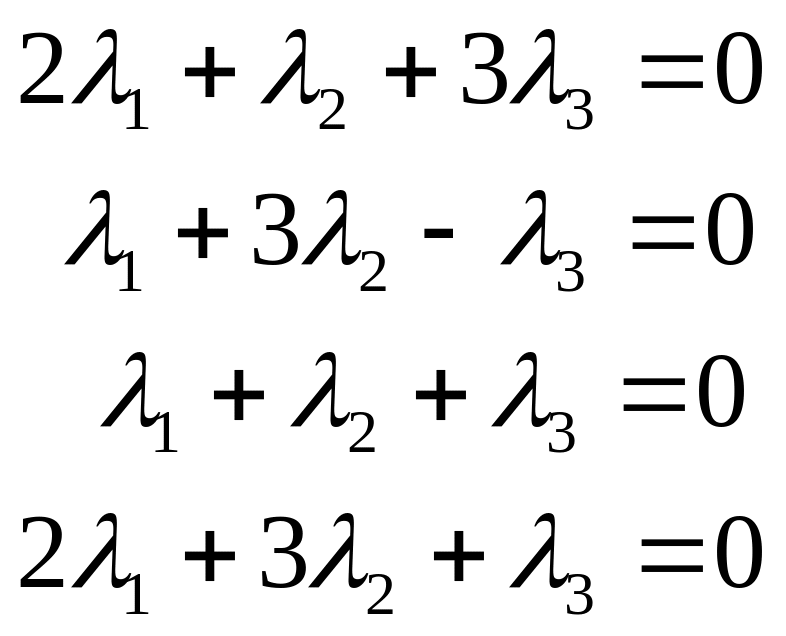
относительно неизвестных .

.

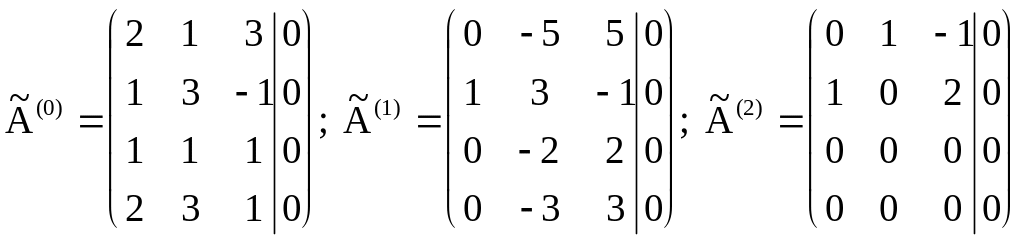Система имеет бесконечное множество решений. Поэтому система векторов является линейно зависимой.

Общее решение имеет вид: .

Подставим общее решение в векторное равенство .

Полагая , получим: , откуда можно любой вектор выразить как линейную комбинацию остальных векторов. Например, или .

В пространстве R_n максимальное число линейно независимых векторов равно n. Любая система из n+1 вектора является линейно зависимой.

Определение. Совокупность n линейно независимых векторов пространства R_n называется его базисом.

Например, базис пространства R_n образуют n единичных векторов , причем i-я координата вектора e_i равна единице, а остальные координаты равны нулю. Данный базис принято называть естественным.

Пример 2.14. В естественном базисе заданы векторы = (1, 1, 0)^т, = (1, -1, 1)^т, = (-3, 5, -6)^т, = (4, -4, 5)^т. Показать, что векторы образуют базис. Выразить вектор в базисе и найти связь между базисом и базисом .

Решение. Векторы образуют базис, если они линейно независимы. Решим векторное уравнение относительно неизвестных :

.

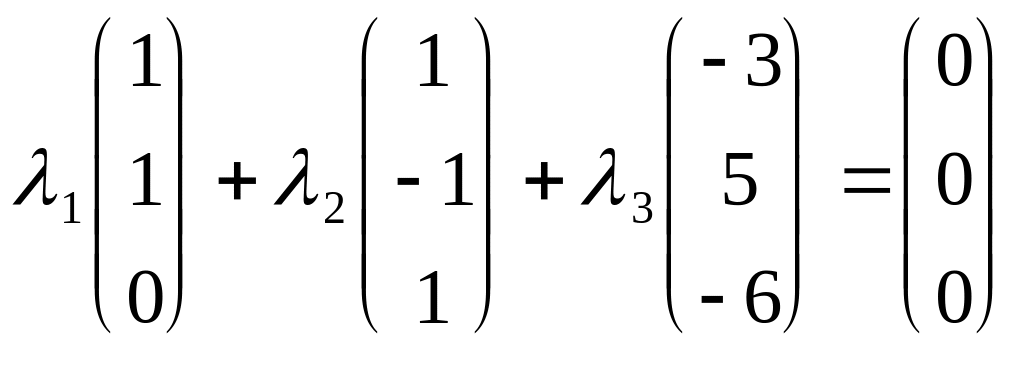Решение данного уравнения единственное, а именно нулевое: . Следовательно, векторы образуют линейно независимую систему векторов и составляют базис.

Выразим связь между базисами и определим координаты вектора в новом базисе:

Выпишем для данных систем расширенную матрицу

.

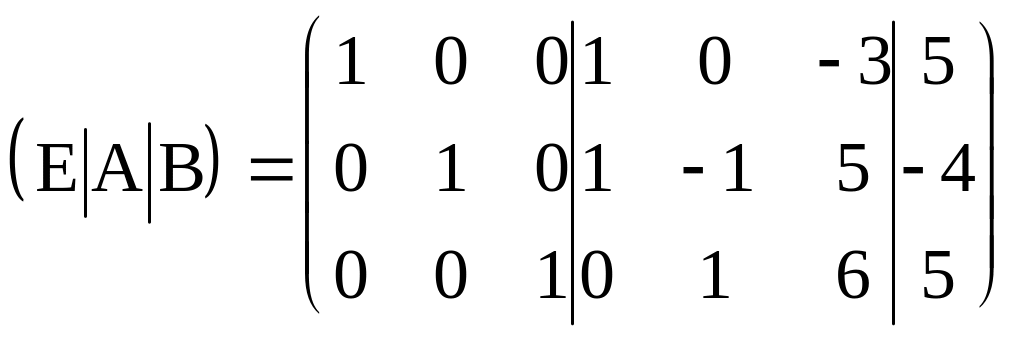Коэффициенты при неизвестных х_ij, х_j (i,j = 1, 3) в системах совпадают. Поэтому методом Жордана–Гаусса находим одновременно решение четырех систем. Все вычисления представим в виде следующей таблицы:

Базис
	1 0 0	0 1 0	0 0 1	1 1 0	1 -1 1	-3 5 -6	4 -4 5
	1 -1 0	0 1 0	0 0 1	1 0 0	1 -2 1	-3 8 -6	4 -8 5
	1/2 1/2 -1/2	1/2 -1/2 1/2	0 0 1	1 0 0	0 1 0	1 -4 -2	0 4 1
	1/4 3/2 1/4	3/4 -3/2 -1/4	1/2 -2 -1/2	1 0 0	0 1 0	0 0 1	1/2 2 -1/2

Матрицу А, составленную из координат векторов , преобразуем в единичную матрицу Е, тогда на месте единичной матрицы Е получим обратную матрицу А^-1. Матрица В преобразуется в матрицу А^-1В. Вектор в новом базисе выражается в виде следующей линейной комбинации векторов нового базиса : .

Связь между старым и новым базисами выражается следующим образом:

.

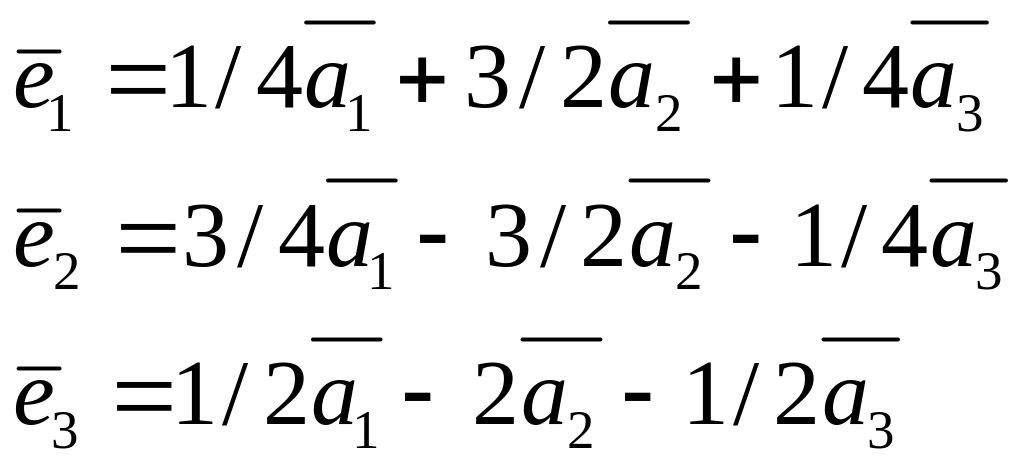Проверка: