2.3. Решение систем алгебраических уравнений

2.3.1. Основные понятия и определения

Рассмотрим систему m линейных уравнений с n неизвестными:

где a_ij, b_i (I = 1, 2,…, m;j = 1, 2,…, n) – произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.

Решением системы линейных уравнений называется совокупность n чисел ( ) – таких, что при подстановке их вместо неизвестных каждое уравнение системы обращается в тождество.

Система линейных уравнений называется совместной, если существует хотя бы одно ее решение. Система, не имеющая ни одного решения, называется несовместной.

Совместные системы подразделяются на определенные, имеющие единственное решение, и неопределенные, имеющие бесконечное множество решений.

Запишем систему в матричной форме. Обозначим:

,

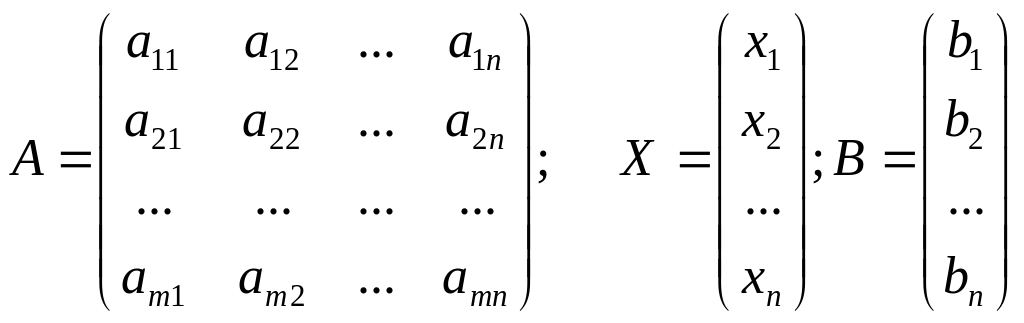где A – матрица коэффициентов при переменных, или матрица системы, X – матрица-столбец переменных; B – матрица-столбец свободных членов.

Так как число столбцов матрицы A равно числу строк матрицы X, то их произведение AX есть матрица-столбец. Элементами этой матрицы-столбца являются левые части системы. На основании определения равенства матриц систему можно записать в матричной форме:

AX = B.

2.3.2. Формулы крамера и метод обратной матрицы

Формулы Крамера применяются при решении системы n линейных уравнений с n неизвестными, определитель которой отличен от нуля.

Решение системы линейных уравнений находится по формулам Крамера:

где |A| — определитель матрицы А, определённой нами выше, |A_j| — определитель, полученный из определителя |A| путем замены j-го столбца столбцом свободных членов.

Пример 2.9. Решить систему уравнений по правилу Крамера:

Х₁ + Х₂ + Х₃ + Х₄ = 10

Х₁ - Х₂ + Х₃ - Х₄ = -2

2Х₁ - 3Х₂ + 4Х₃ + Х₄ = 12

3Х₁ + 4Х₂ - 3Х₃ + 9Х₄ = 38

Решение. Вычислим определитель матрицы A:

.

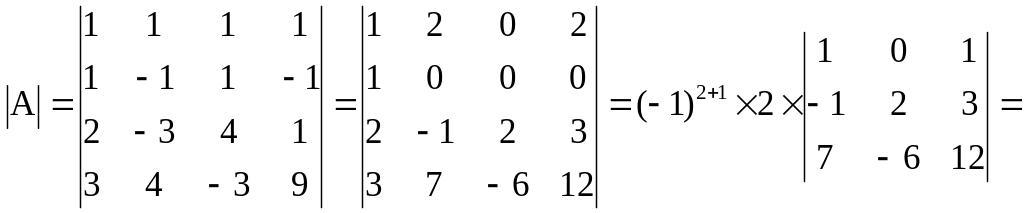
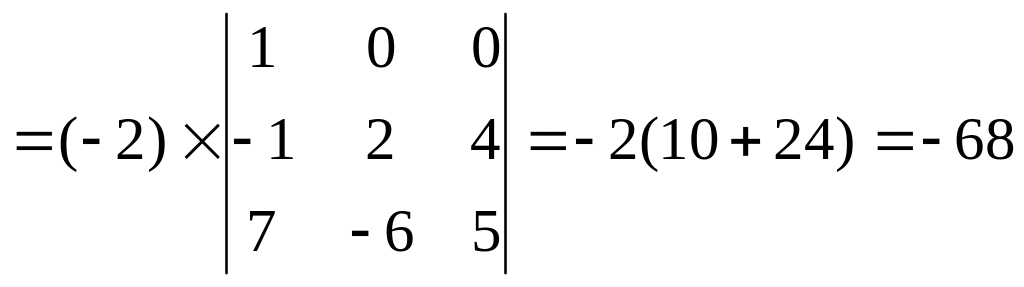Определитель , следовательно, система совместна и обладает единственным решением. Вычислим определители |A_j|, j = 1, …, 4:

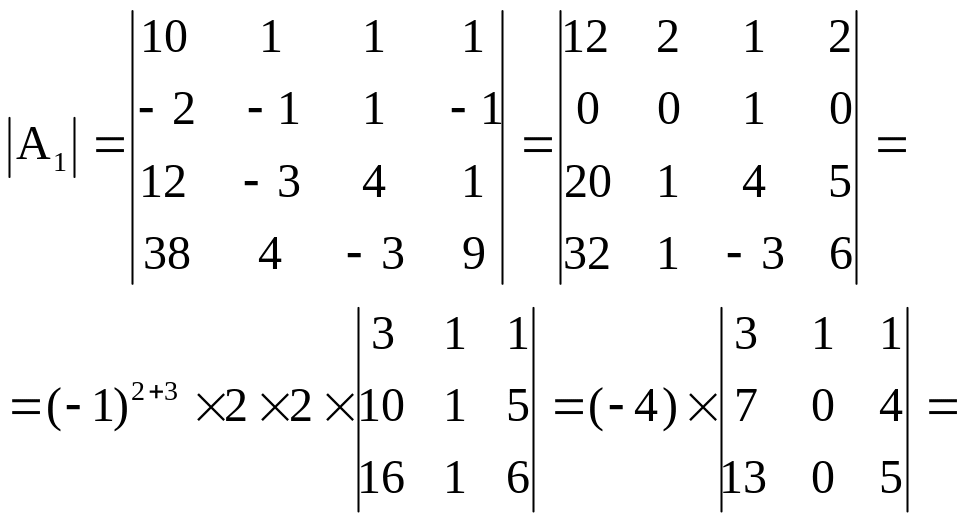
Аналогично вычисляем определители |A₂|, |A₃|, |A₄|: |A₂| = -136, |A₃| = -204, |A₄| = -272. Решение системы имеет вид:

После нахождения решения целесообразно сделать проверку, подставив найденные значения в уравнения системы, и убедиться в том, что они обращаются в верные равенства.

Методом обратной матрицы решаются системы n линейных уравнений с n неизвестными, определитель которых отличен от нуля. Решение матричного уравнения имеет вид: Х = А^-1В (получено из системы, записанной в матричной форме, определённой в пункте 2.3.1.).

Пример 2.10. Решить систему линейных уравнений матричным методом:

3Х₁ – Х₂ = 1

2Х₁ + Х₂ – 3Х₃ = -5

Х₁ + 2Х₂ + Х₃ = 8.

Решение. Представим данную систему в виде матричного уравнения:

.

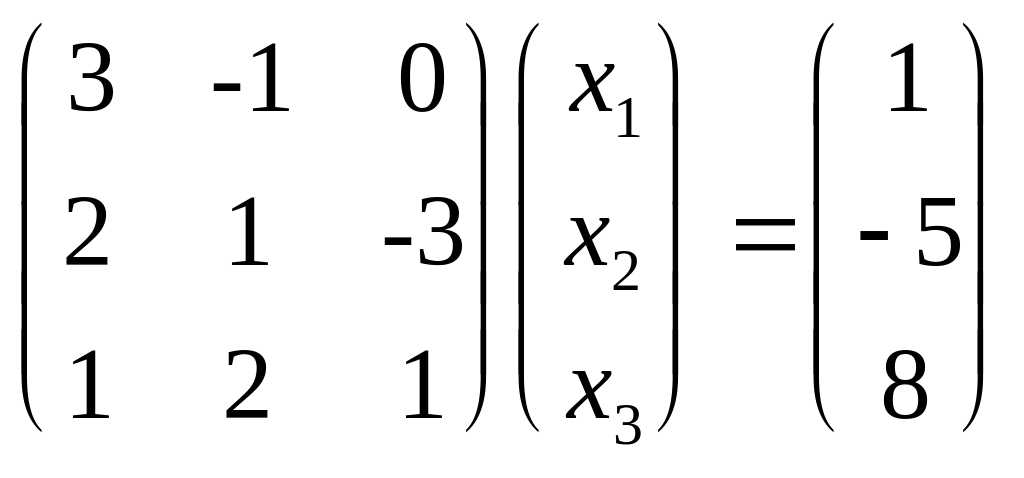Вычислим матрицу, обратную для матрицы А:

.

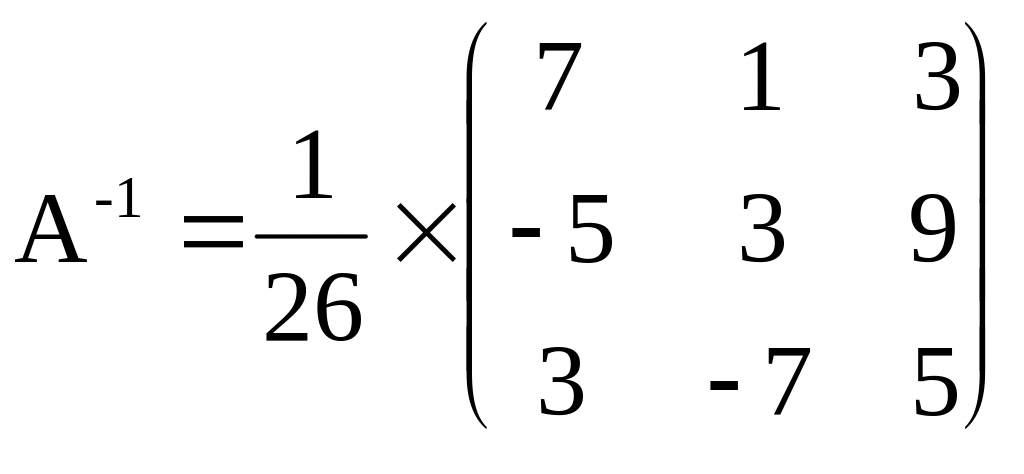Найдем вектор неизвестных Х: 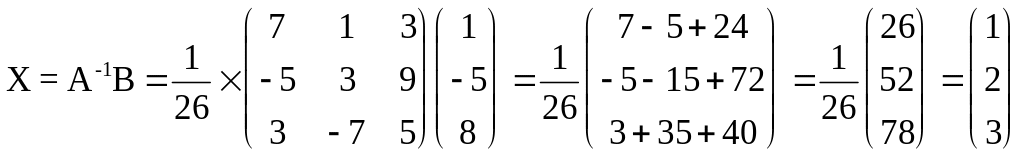. Откуда получаем решение системы: Х₁ = 1, Х₂ = 2, Х₃ = 3.

После нахождения решения целесообразно сделать проверку, подставив найденные значения в уравнения системы, и убедиться в том, что они обращаются в верные равенства.