2.9. Электромагнитті өрістің күшеюі үшін мәжбүрлі ауысуларды қолдану

Жоғарғы энергетикалық деңгейден төменгіге когерентті ауысу кезінде қозған микробөлшектердің мәжбүрлі сәулелену жағдайы мәжбүрлі ауысуларды электромагнитті өрісті күшейту үшін қолданады деген ойға алып келеді. Мұндай күшейтудің мүмкіндігін бағалау үшін заттың және өрістің энергия алмасуын қарастырамыз. Зат N1 және N2 орнығуға, екі Е1 және Е2 энергетикалық деңгейге ие деп есептейік. Ал сыртқы өрістің жиілігі v21 квантты ауысудың жиілігіне тең. Энергияның Пv көлемдік тығыздығы кезінде бірлік көлемдегі бірлік уақытта n21 = BПvN2 энергия бөлінуімен мәжбүрлі ауысулардың саны және е қуаты былайша анықталады:

Энергия жұтылуы бар мәжбүрлі ауысулардың саны сәйкесінше былай болады:

Электромагнитті өрістің қуатының өзгеруі

Р – ны әсерлесу қуаты деп атайық.

Егер Р>0, және де бөлінетін қуат жұтылатыннан асса, онда жүйеде өріс энергиясы өседі немесе электромагнитті өріс күшейеді. Р<0 кезінде энергия жұтылуына иеленеді және сыртқы өріс энергиясы төмендейді.

Осылайша, Р>0 күшейту шарты (N2 – N1) > 0 немесе N2/N1 > 1 болып табылады.

Больцман заңына сәйкес, термодинамикалық теңдік жағдайында жоғарғы деңгейдің орналасуы төменгіге қарағанда төмен болып келеді (N2Б < N1Б). Сондықтан да, зат осындай жағдайда сыртқы өріс энергиясын жұтады (Р < 0), төменнен жоғарыға (1-2) n12 энергия жұтылуы бар кванттық ауысулар саны жоғарыдан төменге (2-1) энергия бөлінуімен n21 квантты ауысулар санынан көп болады.

N2 > N1 қатынасы N2Б < N1Б кездегі термодтнамикалық теңдік жағдайына қатысты кері немесе инверсті болып келеді. Сондықтан да, N2 > N1 кездегі жағдай және де мүмкін күшейтуді деңгейлердің орнығу инверсиясы бар жағдай деп атайды.

Термодинамикалық теңдік үшін Больцман заңын былайша жазған дұрыс:

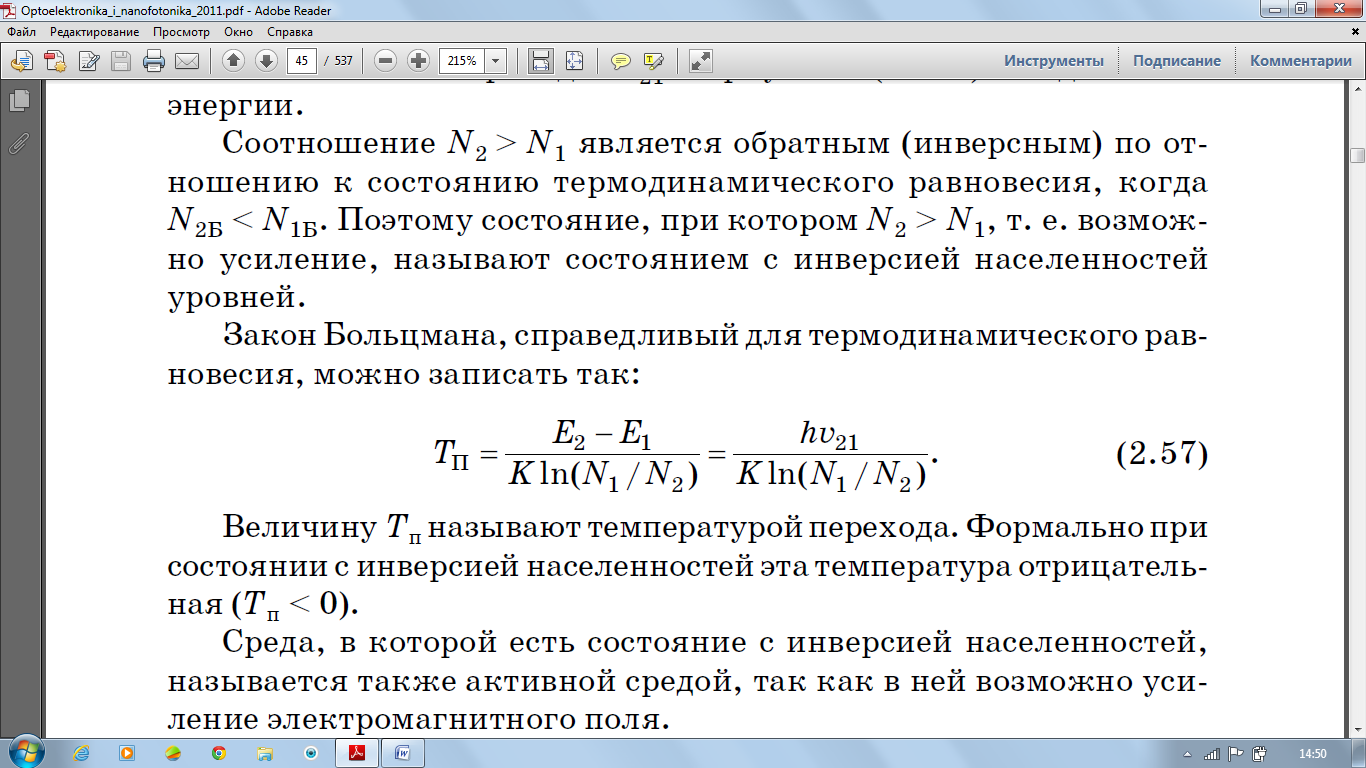
Тп өлшемін ауысу температурасы деп атайды. Орнығу инверсиясы бар жағдай кезінде бұл температура теріс болады (Тп < 0).

Инверсті орнығудағы жағдайы бар орта активті орта деп аталады. Себебі онда электромагнитті өрісті күшейту мүмкіндігі бар.

N1Б > N2Б термодинамикалық тепе-теңдік жағдайында төменгі деңгей орналасуы азаяды, ал жоғарғы деңгейдікі жоғарылайды, сондықтан да, электромагнитті өрістің әсері кезінде төменнен жоғарыға мәжбүрлі ауысулар саны жоғарыдан төменге мәжбүрлі ауысулар санынан жоғары болады. Пvөрісіндегі жеткілікті энергия тығыздығының үлкен көлемі кезінде деңгей орнығуының түзуленуі мүмкін (N1 және N2), мәжбүрлі ауысулардың саны 1 - 2 және 2 – 1 тең болғанда динамикалық тепе-теңдік болады. Орныққан деңгейлерді түзулету құбылысын ауысудың қанығуы деп атайды. Осылайша, екідеңгейлі жүйеге электромагнитті өріс әсер еткенде ауысын инверсиясын емес, ауысудың қанығуына қол жеткізуге болады.

Өріс энергиясының көлемдік тығыздығының кез-келген мәні кезінде деңгейлердің орнығуы жылдамдықтық немесе кинетикалық теңдеулер шешімінен табуға болады. Екідеңгейлік жүйе үшін орнығу деңгейлерінің өзгеру жылдамдықтары үшін:

Бұл жердегі N-бөлшектердің жалпы саны.

Теңдеулерді құру процедураларын анықтайық. Бірлік уақытында 1 деңгейінің орнығуы 1-2 мәжбүрлі ауысуынан N1BПv өлшеміне азаяды, ал 1-2 сәулеленбейтін ауысу әсерінен N1E12 өлшеміне азаяды. Сол уақытта 2-1 ауысуынан N1 орнығуының N2BПv, N1A21 (спонтанды ауысулар) және N2E21 мәніне өсуі жүзеге асады(мәжбүрлі ауысулар). Мәжбүрлі және сәулелендірмейтін ауысулар 1-2 нәтижесінде алғашқы екі қосылғыштарды N2 үлкейткіштері санайды, ал қалғандарын N2 азайтуы мәжбүрлі, спонтанды және сәулелендірмейтін 2-1 ауысулардан анықтайды.

Бөлшектердің жалпы санын сақтау кезінде екі деңгейлі жүйе үшін:

Стационарлы жағдайда

Сондықтан да екі теңдіктің жүйесін былайша жазуға болады:

Теңдеудің бұл жүйесін шеше отырып, N1 және N2 стационарлы өлшемдерді табуға болады, ал кейін олардың қатынасын:

N1 мен N2-нің Пv энергияның көлемдік тығыздығынан тәуелділіктерін Больцман заңымен анықталатын N1Б және N2Б орнығулары бар электромагнитті өріс термодинамикалық тепе-теңдікке орналасқанға дейінгіі жүйе үшін қарастырайық. Пv-ның аз мәні кезінде N1 төменгі деңгейінің орнығуы азаяды, ал N2 жоғарғысы сызықтық заң бойынша жоғарылайды. (Пv-∞) энергия тығыздығының үлкен мәендері кезінде N1 мен N2 ауысулардың қанығуына сәйкес келетін орташа N/2 = (N1Б + N2Б)/2 мәніне ұмтылады.

(Пv = 0) өріс жоқ кезде деңгейлердің орнығуы N 01 және N02 –ге тең, оның үстіне N 02> N 01. Пv N2 –нің өсуімен азаяды, ал N1 сызықты заң бойынша N 01 және N02 мәндерінен өседі. Бірақ, Пv мәні үлкен болғанда олар ауысу қанығуына сәйкес асимптоталық түрде орташа мәнге жақындайды:

(N2 – N1) деңгейлер орнығуының айырмасын Р әсерлесу қуаты анықтайды:

Бұл формула затпен әсерлесетін электромагнитті өрістің әсерлесу қуатының Пv энергияның көлемдік тығыздығынан тәуелділігін анықтауға мүмкіндік береді. P(Пv) тәуелділігі Пv/(1 + δ12П ) қатынасымен анықталады. Пv мәнін үлкейткен кезде, қуат (δ12Пv<<1) алдымен сызықты өседі, ал кейін Рпред мәніне ұмтылады, ол Пv мәні шексіздікке ұмтылған кездегі анықталмағандықты ашу жолымен және де ауысудың қанығу жағдайында анықталады

Әдетте, релаксациялық ауысулардың ықтималдылығы спонтандының ықтималдылығынан әлдеқайда көп екндігін ескере отырып, 2.65. формуласын қарапайым түрде былайша жазуға болады:

Бұл жердегі τрел – релаксация уақыты.

Қанығу жағдайында Пv-∞ (N1 = N2) кезінде 2-1 мәжбүрлі ауысуларда бөлінетін қуат 1-2 мәжбүрлі ауысуы кезіндегі жұтылатын қуатқа тең, электромагнитті өрістен Рпред қуат алынады. Бұл қуат деңгейлердің орнығу тепе-теңдігін сақтап тұру үшін қажет, олар A21, Е21 және Е12 ықтималдылықтары бар мәжбүрлі және сәулелендірмейтін ауысулардың әсерінен үнемі бұзылуға ұмтылып тұрады. Бұл ауысулардың саны энергия тығыздығына тәуелді болмайды және тек деңгей орнығуымен анықталады. Электромагнитті өрістен алынатын энергия затта шашырайды, мысалы, жылу күйдегі кристалдық торда т.б.