6. Практический блок Пример.

Дан временной ряд среднесписочной численности промышленно-производственного персонала промышленности Курской области, тыс. чел.

Годы	1985	1986	1987	1988	1989	1990	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000	2001	2002	2003
y	194,8	194,5	192,9	189,8	189,2	185,6	180,4	180,5	166,8	155,5	146,8	133,4	131,2	124,5	122,3	122,8	121,5	114,5	104,1

Задание:

1. Выбрать модель тренда с помощью диаграммы Excel.

2. Построить технологические таблицы по расчетным значениям и показателям адекватности модели.

3. Оценить устойчивость тенденции.

Параметры уравнения тренда могут быть найдены добавлением линии тренда в диаграмме Excel или решением системы уравнений по МНК.

Рис.6.1 Аппроксимация линейной функцией

Рис.6.2 Аппроксимация параболической функцией

В случае использования уравнения прямой линии согласно МНК:

После преобразований получим систему:

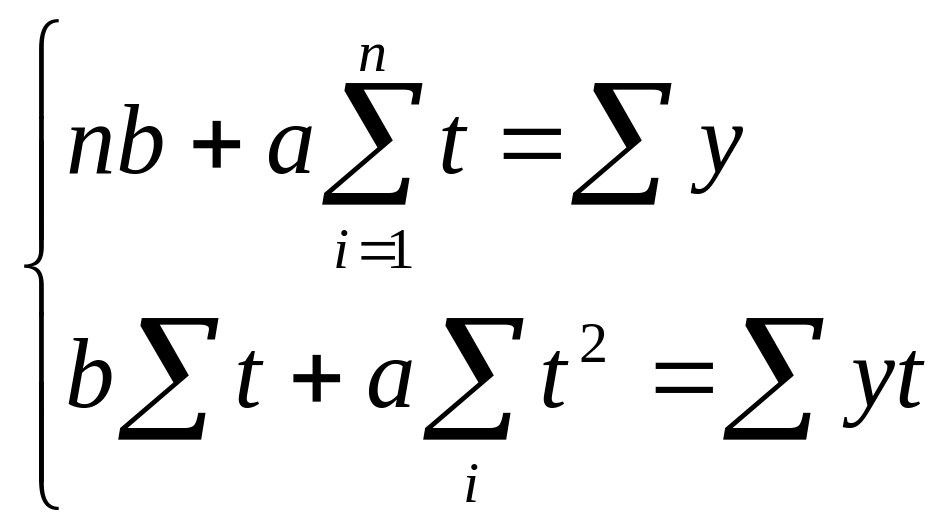
В случае использования уравнения параболы согласно МНК:

Для решения системы без ЭВМ и расчета показателей адекватности составляются технологические таблицы. Решение систем уравнений предполагает расчет необходимых сумм по фактическим данным.

Технологическая таблица расчета показателей

адекватности функции у_t = b+at

t	y	yt	y- yt			(y- yt)2
1	194,8	205,828	11,028	11,028	0,057	121,619
2	194,5	200,216	5,716	5,716	0,029	32,675
3	192,9	194,604	1,704	1,704	0,009	2,905
4	189,8	188,992	-0,808	0,808	0,004	0,652
5	189,2	183,381	-5,820	5,820	0,031	33,867
6	185,6	177,769	-7,831	7,831	0,042	61,331
7	180,4	172,157	-8,243	8,243	0,046	67,952
8	180,5	166,545	-13,955	13,955	0,077	194,748
9	166,8	160,933	-5,867	5,867	0,035	34,423
10	155,5	155,321	-0,179	0,179	0,001	0,032
11	146,8	149,709	2,909	2,909	0,020	8,463
12	133,4	144,097	10,697	10,697	0,080	114,430
13	131,2	138,485	7,285	7,285	0,056	53,076
14	124,5	132,873	8,373	8,373	0,067	70,114
15	122,3	127,262	4,962	4,962	0,041	24,616
16	122,8	121,650	-1,150	1,150	0,009	1,323
17	121,5	116,038	-5,462	5,462	0,045	29,837
18	114,5	110,426	-4,074	4,074	0,036	16,599
19	104,1	104,814	0,714	0,714	0,007	0,510
Сумма					0,692	869,170

- средняя ошибка аппроксимации

Стандартное отклонение:

Технологическая таблица расчета показателей

адекватности функции

t	y	yt	y- yt			(y- yt)2
1	194,8	202,958	8,158	8,158	0,042	66,559
2	194,5	198,304	3,804	3,804	0,020	14,472
3	192,9	193,537	0,637	0,637	0,003	0,406
4	189,8	188,658	-1,142	1,142	0,006	1,304
5	189,2	183,666	-5,534	5,534	0,029	30,625
6	185,6	178,561	-7,039	7,039	0,038	49,542
7	180,4	173,344	-7,056	7,056	0,039	49,784
8	180,5	168,014	-12,486	12,486	0,069	155,890
9	166,8	162,572	-4,228	4,228	0,025	17,876
10	155,5	157,017	1,517	1,517	0,010	2,301
11	146,8	151,349	4,549	4,549	0,031	20,697
12	133,4	145,569	12,169	12,169	0,091	148,089
13	131,2	139,676	8,476	8,476	0,065	71,849
14	124,5	133,671	9,171	9,171	0,074	84,107
15	122,3	127,553	5,253	5,253	0,043	27,594
16	122,8	121,322	-1,478	1,478	0,012	2,183
17	121,5	114,979	-6,521	6,521	0,054	42,521
18	114,5	108,523	-5,977	5,977	0,052	35,720
19	104,1	101,955	-2,145	2,145	0,021	4,601
Сумма					0,723	826,123

Стандартное отклонение:

Сравним уравнения трендов по показателям адекватности.

Уравнения трендов
	0,954	3,64%	7,15
	0,956	3,81%	7,19

По показателям адекватности выбираем функцию у_t = b+at, которую будем использовать для расчета показателей колеблемости и устойчивости.

Показатель колеблемости равен

Показатель устойчивости -

Показатель устойчивости характеризует близость фактических уровней к тренду на 95,4%.

2.Для оценки устойчивости уровней временного ряда как процесса их направленного изменения рассчитаем коэффициент корреляции рангов Ч.Спирмэна:

, где

n – число уровней временного ряда;

- разность рангов уровней и номеров периодов времени.

t	y	Ранг (y)
1	194,8	19	18	324
2	194,5	18	16	256
3	192,9	17	14	196
4	189,8	16	12	144
5	189,2	15	10	100
6	185,6	14	8	64
7	180,4	12	5	25
8	180,5	13	5	25
9	166,8	11	2	4
10	155,5	10	0	0
11	146,8	9	-2	4
12	133,4	8	-4	16
13	131,2	7	-6	36
14	124,5	6	-8	64
15	122,3	4	-11	121
16	122,8	5	-11	121
17	121,5	3	-14	196
18	114,5	2	-16	256
19	104,1	1	-18	324
Сумма				2276

Коэффициент Спирмена , достаточно близок к -1, что доказывает устойчивость снижения показателей ряда.

Контрольные вопросы

1. Трендовые модели с независимыми значениями случайной составляющей.

2. Полиномиальный тренд.

3. Трендовые модели с сезонными колебаниями.

4. В чем суть метода экспоненциального сглаживания?

5. В чем заключается проблема автокорреляции остатков и как она проявляется?

6. В чем состоит специфика построения моделей регрессии по временным рядам данных?

7. Перечислите основные методы исключения тенденции. Сравните их преимущества и недостатки.

8. Изложите суть метода отклонений от тренда.

9. В чем сущность метода последовательных разностей?

10. Какова интерпретация параметра при факторе времени в моделях регрессии с включением фактора времени?

11. Охарактеризуйте понятие автокорреляции в остатках. Какими причинами может быть вызвана автокорреляция в остатках?

12. Что такое критерий Дарбина – Уотсона? Изложите алгоритм его применения для тестирования модели регрессии на автокорреляцию в остатках.

13. Перечислите основные этапы обобщенного МНК.

14. Приведите примеры экономических задач, эконометрическое моделирование которых требует применения моделей с распределенным лагом и моделей авторегрессии.

15. Какова интерпретация параметров модели с распределенным лагом?

16. Какова интерпретация параметров модели авторегрессии?

17. Изложите методику применения метода инструментальных переменных для оценки параметров модели авторегрессии.

18. Изложите методику тестирования модели авторегрессии на автокорреляцию в остатках.